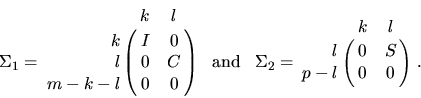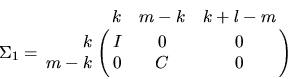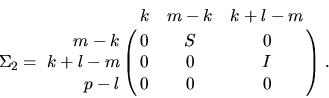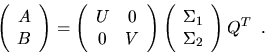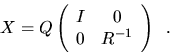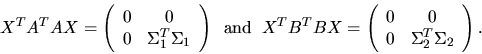Next: Computational Routines
Up: Generalized Eigenvalue and Singular
Previous: Generalized Nonsymmetric Eigenproblems (GNEP)
Contents
Index
Generalized Singular Value Decomposition (GSVD)
The generalized (or quotient) singular value decomposition
of an m-by-n matrix A and a
p-by-n matrix B is given by the pair of factorizations
The matrices in these factorizations have the following properties:
- U is m-by-m, V is p-by-p, Q is n-by-n, and
all three matrices are orthogonal. If A and
B are complex, these matrices are unitary instead of
orthogonal, and QT should be
replaced by QH in the pair of factorizations.
- R is r-by-r, upper triangular and nonsingular.
[0,R] is r-by-n (in other words, the 0 is an r-by-n-r
zero matrix).
The integer r is the rank of
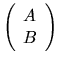 ,
and satisfies
,
and satisfies 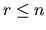 .
.
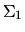 is m-by-r,
is m-by-r,
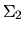 is p-by-r, both are real, nonnegative and diagonal, and
is p-by-r, both are real, nonnegative and diagonal, and
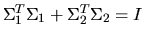 .
Write
.
Write
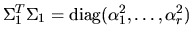 and
and
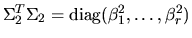 ,
where
,
where 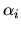 and
and 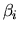 lie in the interval from 0 to 1.
The ratios
lie in the interval from 0 to 1.
The ratios
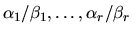 are called the generalized singular values of the pair A, B.
If
are called the generalized singular values of the pair A, B.
If 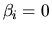 ,
then the generalized singular value
,
then the generalized singular value
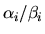 is infinite.
is infinite.
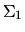 and
and 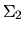 have the following detailed
structures, depending on whether
have the following detailed
structures, depending on whether 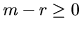 or
m-r < 0. In the first case,
or
m-r < 0. In the first case, 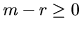 ,
then
,
then
Here l is the rank of B, k=r-l, C and S are diagonal
matrices satisfying
C2 + S2 = I, and S is nonsingular.
We may also identify
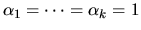 ,
,
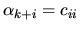 for
for
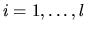 ,
,
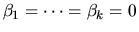 ,
and
,
and
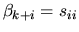 for
for
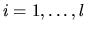 .
Thus, the first k generalized singular values
.
Thus, the first k generalized singular values
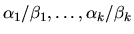 are infinite, and the remaining l generalized singular values
are finite.
are infinite, and the remaining l generalized singular values
are finite.
In the second case, when m-r < 0,
and
Again, l is the rank of B, k=r-l, C and S are diagonal
matrices satisfying C2 + S2 = I, S is nonsingular,
and we may identify
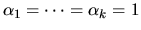 ,
,
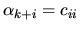 for
for
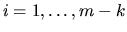 ,
,
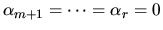 ,
,
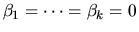 ,
,
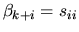 for
for
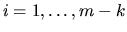 ,
and
,
and
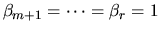 .
Thus, the first k generalized singular values
.
Thus, the first k generalized singular values
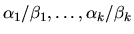 are infinite, and the remaining l generalized singular values
are finite.
are infinite, and the remaining l generalized singular values
are finite.
Here are some important special cases of the generalized singular value
decomposition.
First, if B is square and nonsingular, then r=n and the
generalized singular value decomposition of A and B is equivalent
to the singular value decomposition of AB-1, where the singular
values of AB-1 are equal to the generalized singular values of the
pair A, B:
Second, if
the columns of
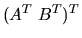 are orthonormal, then r=n, R=I and the
generalized
singular value decomposition of A and B is equivalent to the CS
(Cosine-Sine) decomposition of
are orthonormal, then r=n, R=I and the
generalized
singular value decomposition of A and B is equivalent to the CS
(Cosine-Sine) decomposition of
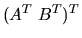 [55]:
[55]:
Third, the generalized eigenvalues and eigenvectors of
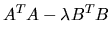 can be expressed in terms of the generalized singular value decomposition:
Let
can be expressed in terms of the generalized singular value decomposition:
Let
Then
Therefore, the columns of X are the eigenvectors of
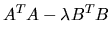 ,
and the ``nontrivial'' eigenvalues are the
squares of the generalized singular values (see also section 2.3.5.1).
``Trivial'' eigenvalues
are those corresponding to the leading n-r columns of X,
which span the common null space of AT A and BT B.
The ``trivial eigenvalues'' are not well defined2.1.
,
and the ``nontrivial'' eigenvalues are the
squares of the generalized singular values (see also section 2.3.5.1).
``Trivial'' eigenvalues
are those corresponding to the leading n-r columns of X,
which span the common null space of AT A and BT B.
The ``trivial eigenvalues'' are not well defined2.1.
A single driver routine xGGSVD computes the generalized
singular value decomposition of A and B (see Table 2.6).
The method is based on the method described in
[83,10,8].
Table 2.6:
Driver routines for generalized eigenvalue and singular value problems
| Type of |
Function and storage scheme |
Single precision |
Double precision |
| problem |
|
real |
complex |
real |
complex |
| GSEP |
simple driver |
SSYGV |
CHEGV |
DSYGV |
ZHEGV
|
| |
divide and conquer driver |
SSYGVD |
CHEGVD |
DSYGVD |
ZHEGVD
|
| |
expert driver |
SSYGVX |
CHEGVX |
DSYGVX |
ZHEGVX
|
| |
simple driver (packed storage) |
SSPGV |
CHPGV |
DSPGV |
ZHPGV
|
| |
divide and conquer driver |
SSPGVD |
CHPGVD |
DSPGVD |
ZHPGVD
|
| |
expert driver |
SSPGVX |
CHPGVX |
DSPGVX |
ZHPGVX
|
| |
simple driver (band matrices) |
SSBGV |
CHBGV |
DSBGV |
ZHBGV
|
| |
divide and conquer driver |
SSBGVD |
CHBGVD |
DSBGV |
ZHBGVD
|
| |
expert driver |
SSBGVX |
CHBGVX |
DSBGVX |
ZHBGVX
|
| GNEP |
simple driver for Schur factorization |
SGGES |
CGGES |
DGGES |
ZGGES
|
| |
expert driver for Schur factorization |
SGGESX |
CGGESX |
DGGESX |
ZGGESX
|
| |
simple driver for eigenvalues/vectors |
SGGEV |
CGGEV |
DGGEV |
ZGGEV
|
| |
expert driver for eigenvalues/vectors |
SGGEVX |
CGGEVX |
DGGEVX |
ZGGEVX
|
| GSVD |
singular values/vectors |
SGGSVD |
CGGSVD |
DGGSVD |
ZGGSVD
|





Next: Computational Routines
Up: Generalized Eigenvalue and Singular
Previous: Generalized Nonsymmetric Eigenproblems (GNEP)
Contents
Index
Susan Blackford
1999-10-01
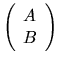 ,
and satisfies
,
and satisfies ![]() and
and ![]() have the following detailed
structures, depending on whether
have the following detailed
structures, depending on whether ![]() or
m-r < 0. In the first case,
or
m-r < 0. In the first case, ![]() ,
then
,
then