Generalized Nonsymmetric Eigenproblems (GNEP)

Given a matrix pair (A, B), where A and B are square n x n matrices, the generalized nonsymmetric eigenvalue problem is to find the eigenvalues $\lambda$ and corresponding eigenvectors $x \not= 0$ such that

$$A x = \lambda B x ,$$

or to find the eigenvalues $\mu$ and corresponding eigenvectors $y \not= 0$ such that

$$\mu A y = B y.$$

Note that these problems are equivalent with $\mu = 1/\lambda$ and x=y if neither $\lambda$ nor $\mu$ is zero. In order to deal with the case that $\lambda$ or $\mu$ is zero, or nearly so, the LAPACK routines return two values, $\alpha$ and $\beta$, for each eigenvalue, such that $\lambda = \alpha/\beta$ and $\mu = \beta/\alpha$.

More precisely, x and y are called right eigenvectors. Vectors $u \not= 0$ or $v \not= 0$ satisfying

$$u^H A = \lambda u^H B \quad\mbox{or}\quad \mu v^H A = v^H B$$

are called left eigenvectors.

Sometimes the following, equivalent notation is used to refer to the generalized eigenproblem for the pair (A,B): The object $A - \lambda B$, where $\lambda$ is an indeterminate, is called a matrix pencil, or just pencil. So one can also refer to the generalized eigenvalues and eigenvectors of the pencil $A - \lambda B$.

If the determinant of $A - \lambda B$ is identically zero for all values of $\lambda$, the eigenvalue problem is called singular; otherwise it is regular. Singularity of (A,B) is signaled by some $\alpha = \beta = 0$ (in the presence of roundoff, $\alpha$ and $\beta$ may be very small). In this case, the eigenvalue problem is very ill-conditioned, and in fact some of the other nonzero values of $\alpha$ and $\beta$ may be indeterminate (see section 4.11.1.4 for further discussion) [93,105,29]. The current routines in LAPACK are intended only for regular matrix pencils.

The generalized nonsymmetric eigenvalue problem can be solved via the generalized Schur decomposition of the matrix pair (A, B), defined in the real case as

$$A = Q S Z^T, \quad B = Q T Z^T$$

where Q and Z are orthogonal matrices, T is upper triangular, and S is an upper quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks, the 2-by-2 blocks corresponding to complex conjugate pairs of eigenvalues of (A, B). In the complex case, the generalized Schur decomposition is

$$A = Q S Z^H, \quad B = Q T Z^H$$

where Q and Z are unitary and S and T are both upper triangular.

The columns of Q and Z are called left and right generalized Schur vectors and span pairs of deflating subspaces of A and B [93]. Deflating subspaces are a generalization of invariant subspaces: For each k $(1 \leq k \leq n)$, the first k columns of Z span a right deflating subspace mapped by both A and B into a left deflating subspace spanned by the first k columns of Q.

More formally, let Q = (Q₁, Q₂) and Z = (Z₁, Z₂) be a conformal partitioning with respect to the cluster of k eigenvalues in the (1,1)-block of (S, T), i.e. where Q₁ and Z₁ both have k columns, and S₁₁ and T₁₁ below are both k-by-k,

$$\left( \begin{array}{c} Q^H_1 \\ Q^H_2 \end{array} \right) ... ...rray}{cc} T_{11} & T_{12} \\ 0 & T_{22} \end{array} \right).$$

Then subspaces ${\cal{L}} = \mbox{span}(Q_1)$ and ${\cal{R}} = \mbox{span}(Z_1)$ form a pair of (left and right) deflating subspaces associated with the cluster of (S₁₁,T₁₁), satisfying ${\cal{L}} = A{\cal{R}} + B{\cal{R}}$ and $\mbox{dim}(\cal{L}) = \mbox{dim}(\cal{R})$ [94,95]. It is possible to order the generalized Schur form so that (S₁₁, T₁₁) has any desired subset of k eigenvalues, taken from the set of n eigenvalues of (S,T).

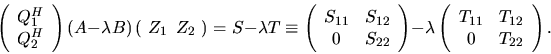
As for the standard nonsymmetric eigenproblem, two pairs of drivers are provided, one pair focusing on the generalized Schur decomposition, and the other pair on the eigenvalues and eigenvectors as shown in Table 2.6:

• xGGES: a simple driver that computes all or part of the generalized Schur decomposition of (A, B), with optional ordering of the eigenvalues;

• xGGESX: an expert driver that can additionally compute condition numbers for the average of a selected subset of eigenvalues, and for the corresponding pair of deflating subspaces;

• xGGEV: a simple driver that computes all the generalized eigenvalues of (A, B), and optionally the left or right eigenvectors (or both);

• xGGEVX: an expert driver that can additionally balance the matrix pair to improve the conditioning of the eigenvalues and eigenvectors, and compute condition numbers for the eigenvalues and/or left and right eigenvectors (or both).

To save space in Table 2.6, the word ``generalized'' is omitted before Schur decomposition, eigenvalues/vectors and singular values/vectors.

The subroutines xGGES and xGGEV are improved versions of the drivers, xGEGS and xGEGV, respectively. xGEGS and xGEGV have been retained for compatibility with Release 2.0 of LAPACK, but we omit references to these routines in the remainder of this users' guide.