Bibliography

1

E. ANDERSON, Z. BAI, C. BISCHOF, J. DEMMEL, J. DONGARRA, J. DU CROZ, A. GREENBAUM, S. HAMMARLING, A. MCKENNEY, AND D. SORENSEN, LAPACK: A portable linear algebra library for high-performance computers, Computer Science Dept. Technical Report CS-90-105, University of Tennessee, Knoxville, TN, May 1990.
(Also LAPACK Working Note #20).

2

E. ANDERSON, Z. BAI, AND J. DONGARRA, Generalized QR factorization and its applications, Linear Algebra and Its Applications, 162-164 (1992), pp. 243-271.
(Also LAPACK Working Note #31).

3

E. ANDERSON, J. DONGARRA, AND S. OSTROUCHOV, Installation guide for LAPACK, Computer Science Dept. Technical Report CS-92-151, University of Tennessee, Knoxville, TN, March 1992.
(Also LAPACK Working Note #41).

4

ANSI/IEEE, IEEE Standard for Binary Floating Point Arithmetic, New York, Std 754-1985 ed., 1985.

5

ANSI/IEEE, IEEE Standard for Radix Independent Floating Point Arithmetic, New York, Std 854-1987 ed., 1987.

6

M. ARIOLI, J. W. DEMMEL, AND I. S. DUFF, Solving sparse linear systems with sparse backward error, SIAM J. Matrix Anal. Appl., 10 (1989), pp. 165-190.

7

M. ARIOLI, I. S. DUFF, AND P. P. M. DE RIJK, On the augmented system approach to sparse least squares problems, Num. Math., 55 (1989), pp. 667-684.

8

Z. BAI, , AND H. ZHA, A new preprocessing algorithm for the computation of the generalized singular value decomposition, SIAM J. Sci. Comp., 14 (1993), pp. 1007-1012.

9

Z. BAI AND J. W. DEMMEL, On a block implementation of Hessenberg multishift QR iteration, International Journal of High Speed Computing, 1 (1989), pp. 97-112.
(Also LAPACK Working Note #8).

10

Z. BAI AND J. W. DEMMEL, Computing the generalized singular value decomposition, SIAM J. Sci. Comp., 14 (1993), pp. 1464-1486.
(Also LAPACK Working Note #46).

11

Z. BAI AND J. W. DEMMEL, Design of a parallel nonsymmetric eigenroutine toolbox, Part I, in Proceedings of the Sixth SIAM Conference on Parallel Processing for Scientific Computing, R. F. et al. Sincovec, ed., Philadelphia, PA, 1993, Society for Industrial and Applied Mathematics, pp. 391-398.
Long version available as Computer Science Report CSD-92-718, University of California, Berkeley, 1992.

12

Z. BAI, J. W. DEMMEL, AND A. MCKENNEY, On computing condition numbers for the nonsymmetric eigenproblem, ACM Trans. Math. Softw., 19 (1993), pp. 202-223.
(LAPACK Working Note #13).

13

Z. BAI AND M. FAHEY, Computation of error bounds in linear least squares problems with equality constraints and generalized linear model problems.
to appear, 1997.

14

J. BARLOW AND J. DEMMEL, Computing accurate eigensystems of scaled diagonally dominant matrices, SIAM J. Num. Anal., 27 (1990), pp. 762-791.
(Also LAPACK Working Note #7).

15

J. BILMES, K. ASANOVIC, J. DEMMEL, D. LAM, AND C. CHIN, Optimizing matrix multiply using PHiPAC: A portable, high-performance, ANSI C coding methodology, Computer Science Dept. Technical Report CS-96-326, University of Tennessee, Knoxville, TN, 1996.
(Also LAPACK Working Note #111).

16

Å. BJ¨ORCK, Numerical Methods for Least Squares Problem, SIAM, 1996.

17

L. S. BLACKFORD, J. CHOI, A. CLEARY, E. D'AZEVEDO, J. DEMMEL, I. DHILLON, J. DONGARRA, S. HAMMARLING, G. HENRY, A. PETITET, K. STANLEY, D. WALKER, AND R. C. WHALEY, ScaLAPACK Users' Guide, Society for Industrial and Applied Mathematics, Philadelphia, PA, 1997.

18

A. J. COX AND N. J. HIGHAM, Backward error bounds for constrained least squares problems, BIT, 39 (1999), pp. 210-227.

19

C. R. CRAWFORD, Reduction of a band-symmetric generalized eigenvalue problem, Comm. ACM, 16 (1973), pp. 41-44.

20

J. J. M. CUPPEN, A divide and conquer method for the symmetric tridiagonal eigenproblem, Numerische Math., 36 (1981), pp. 177-195.

21

M. DAYDE, I. DUFF, AND A. PETITET, A Parallel Block Implementation of Level 3 BLAS for MIMD Vector Processors, ACM Trans. Math. Softw., 20 (1994), pp. 178-193.

22

B. DE MOOR AND P. VAN DOOREN, Generalization of the singular value and QR decompositions, SIAM J. Matrix Anal. Appl., 13 (1992), pp. 993-1014.

23

P. DEIFT, J. W. DEMMEL, L.-C. LI, AND C. TOMEI, The bidiagonal singular values decomposition and Hamiltonian mechanics, SIAM J. Numer. Anal., 28 (1991), pp. 1463-1516.
(LAPACK Working Note #11).

24

J. DEMMEL, Underflow and the reliability of numerical software, SIAM J. Sci. Stat. Comput., 5 (1984), pp. 887-919.

25

J. DEMMEL, Applied Numerical Linear Algebra, SIAM, Philadelphia, PA, 1997.

26

J. W. DEMMEL, The condition number of equivalence transformations that block diagonalize matrix pencils, SIAM J. Numer. Anal., 20 (1983), pp. 599-610.

27

J. W. DEMMEL AND N. J. HIGHAM, Stability of block algorithms with fast level 3 BLAS, ACM Trans. Math. Softw., 18 (1992), pp. 274-291.
(Also LAPACK Working Note #22).

28

J. W. DEMMEL AND N. J. HIGHAM, Improved error bounds for underdetermined systems solvers, SIAM J. Matrix Anal. Appl., 14 (1993), pp. 1-14.
(Also LAPACK Working Note #23).

29

J. W. DEMMEL AND B. KÅGSTR¨OM, Computing stable eigendecompositions of matrix pencils, Lin. Alg. Appl., 88/89 (1987), pp. 139-186.

30

J. W. DEMMEL AND B. KÅGSTR¨OM, The generalized Schur decomposition of an arbitrary pencil 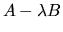$A - \lambda B$: robust software with error bounds and applications, part I: Theory and algorithms, ACM Trans. Math. Softw., 19 (1993), pp. 160-174.

31

J. W. DEMMEL AND B. KÅGSTR¨OM, The generalized Schur decomposition of an arbitrary pencil 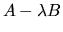$A - \lambda B$: robust software with error bounds and applications, part II: Software and applications, ACM Trans. Math. Softw., 19 (1993), pp. 175-201.

32

J. W. DEMMEL AND W. KAHAN, Accurate singular values of bidiagonal matrices, SIAM J. Sci. Stat. Comput., 11 (1990), pp. 873-912.
(Also LAPACK Working Note #3).

33

J. W. DEMMEL AND X. LI, Faster numerical algorithms via exception handling, IEEE Trans. Comp., 43 (1994), pp. 983-992.
(Also LAPACK Working Note #59).

34

J. W. DEMMEL AND K. VESELI´C, Jacobi's method is more accurate than QR, SIAM J. Matrix Anal. Appl., 13 (1992), pp. 1204-1246.
(Also LAPACK Working Note #15).

35

I. DHILLON, A new O(n²) algorithm for the symmetric tridiagonal eigenvalue/eigenvector problem, Computer Science Division Technical Report no. UCB/CSD-97-971, University of California, Berkeley, CA, May 1997.

36

I. S. DHILLON AND B. N. PARLETT, Orthogonal eigenvectors and relative gaps, June 1999.
to appear.

37

J. DONGARRA AND S. OSTROUCHOV, Quick installation guide for LAPACK on unix systems, Computer Science Dept. Technical Report CS-94-249, University of Tennessee, Knoxville, TN, September 1994.
(LAPACK Working Note #81).

38

J. J. DONGARRA, J. R. BUNCH, C. B. MOLER, AND G. W. STEWART, LINPACK Users' Guide, Society for Industrial and Applied Mathematics, Philadelphia, PA, 1979.

39

J. J. DONGARRA, J. DU CROZ, I. S. DUFF, AND S. HAMMARLING, Algorithm 679: A set of Level 3 Basic Linear Algebra Subprograms, ACM Trans. Math. Soft., 16 (1990), pp. 18-28.

40

J. J. DONGARRA, J. DU CROZ, I. S. D UFF, AND S. HAMMARLING, A set of Level 3 Basic Linear Algebra Subprograms, ACM Trans. Math. Soft., 16 (1990), pp. 1-17.

41

J. J. DONGARRA, J. DU CROZ, S. HAMMARLING, AND R. J. HANSON, Algorithm 656: An extended set of FORTRAN Basic Linear Algebra Subroutines, ACM Trans. Math. Soft., 14 (1988), pp. 18-32.

42

J. J. DONGARRA, J. DU CROZ, S. HAMMARLING, AND R. J. HANSON, An extended set of FORTRAN basic linear algebra subroutines, ACM Trans. Math. Soft., 14 (1988), pp. 1-17.

43

J. J. DONGARRA, I. S. DUFF, D. C. SORENSEN, AND H. A. VAN DER VORST, Numerical Linear Algebra for High-Performance Computers, Society for Industrial and Applied Mathematics, Philadelphia, PA, 1998.

44

J. J. DONGARRA AND E. GROSSE, Distribution of mathematical software via electronic mail, Communications of the ACM, 30 (1987), pp. 403-407.

45

J. J. DONGARRA, F. G. GUSTAFSON, AND A. KARP, Implementing linear algebra algorithms for dense matrices on a vector pipeline machine, SIAM Review, 26 (1984), pp. 91-112.

46

J. J. DONGARRA, S. HAMMARLING, AND D. C. SORENSEN, Block reduction of matrices to condensed forms for eigenvalue computations, JCAM, 27 (1989), pp. 215-227.
(LAPACK Working Note #2).

47

J. DU CROZ AND N. J. HIGHAM, Stability of methods for matrix inversion, IMA J. Numer. Anal., 12 (1992), pp. 1-19.
(Also LAPACK Working Note #27).

48

J. DU CROZ, P. J. D. MAYES, AND G. RADICATI DI BROZOLO, Factorizations of band matrices using Level 3 BLAS, Computer Science Dept. Technical Report CS-90-109, University of Tennessee, Knoxville, TN, 1990.
(LAPACK Working Note #21).

49

A. DUBRULLE, The multishift QR algorithm: is it worth the trouble?, Palo Alto Scientific Center Report G320-3558x, IBM Corp., 1530 Page Mill Road, Palo Alto, CA 94304, 1991.

50

L. ELD´EN, Perturbation theory for the least squares problem with linear equality constraints, SIAM J. Numer. Anal., 17 (1980), pp. 338-350.

51

V. FERNANDO AND B. PARLETT, Accurate singular values and differential qd algorithms, Numerisch Math., 67 (1994), pp. 191-229.

52

K. A. GALLIVAN, R. J. PLEMMONS, AND A. H. SAMEH, Parallel algorithms for dense linear algebra computations, SIAM Review, 32 (1990), pp. 54-135.

53

F. GANTMACHER, The Theory of Matrices, vol. II (transl.), Chelsea, New York, 1959.

54

B. S. GARBOW, J. M. BOYLE, J. J. DONGARRA, AND C. B. MOLER, Matrix Eigensystem Routines - EISPACK Guide Extension, vol. 51 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 1977.

55

G. GOLUB AND C. F. VAN LOAN, Matrix Computations, Johns Hopkins University Press, Baltimore, MD, third ed., 1996.

56

A. GREENBAUM AND J. J. DONGARRA, Experiments with QL/QR methods for the symmetric tridiagonal eigenproblem, Computer Science Dept. Technical Report CS-89-92, University of Tennessee, Knoxville,TN, 1989.
(LAPACK Working Note #17).

57

M. GU AND S. EISENSTAT, A stable algorithm for the rank-1 modification of the symmetric eigenproblem, Computer Science Department Report YALEU/DCS/RR-916, Yale University, New Haven, CT, 1992.

58

M. GU AND S. EISENSTAT, A divide-and-conquer algorithm for the bidiagonal SVD, SIAM J. Mat. Anal. Appl., 16 (1995), pp. 79-92.

59

W. W. HAGER, Condition estimators, SIAM J. Sci. Stat. Comput., 5 (1984), pp. 311-316.

60

S. HAMMARLING, The numerical solution of the general Gauss-Markov linear model, in Mathematics in Signal Processing, T. S. et al.. Durani, ed., Clarendon Press, Oxford, UK, 1986.

61

N. J. HIGHAM, Efficient algorithms for computing the condition number of a tridiagonal matrix, SIAM J. Sci. Stat. Comput., 7 (1986), pp. 150-165.

62

N. J. HIGHAM, A survey of condition number estimation for triangular matrices, SIAM Review, 29 (1987), pp. 575-596.

63

N. J. HIGHAM, FORTRAN codes for estimating the one-norm of a real or complex matrix, with applications to condition estimation, ACM Trans. Math. Softw., 14 (1988), pp. 381-396.

64

N. J. HIGHAM, Algorithm 674: FORTRAN codes for estimating the one-norm of a real or complex matrix, with applications to condition estimation, ACM Trans. Math. Softw., 15 (1989), p. 168.

65

N. J. HIGHAM, Experience with a matrix norm estimator, SIAM J. Sci. Stat. Comput., 11 (1990), pp. 804-809.

66

N. J. HIGHAM, Perturbation theory and backward error for AX-XB=C, BIT, 33 (1993), pp. 124-136.

67

N. J. HIGHAM, Accuracy and Stability of Numerical Algorithms, SIAM, Philadelphia, PA, 1996.

68

S. HUSS-LEDERMAN, A. TSAO, AND G. ZHANG, A parallel implementation of the invariant subspace decomposition algorithm for dense symmetric matrices, in Proceedings of the Sixth SIAM Conference on Parallel Processing for Scientific Computing, Society for Industrial and Applied Mathematics, 1993, pp. 367-374.

69

E. JESSUP AND D. SORENSEN, A parallel algorithm for computing the singular value decomposition of a matrix, Mathematics and Computer Science Division Report ANL/MCS-TM-102, Argonne National Laboratory, Argonne, IL, December 1987.

70

B. KÅGSTRÖM, A direct method for reordering eigenvalues in the generalized real Schur form of a regular matrix pair (a,b), in Linear Algebra for Large Scale and Real-Time Applications, Kluwer Academic Publishers, 1993, pp. 195-218.

71

B. KÅGSTRÖM, A perturbation analysis of the generalized sylvester equation, SIAM J. Matrix Anal. Appl., 15 (1994), pp. 1045-1060.

72

B. KÅGSTR¨OM, P. LING, AND C. V. LOAN, GEMM-based level 3 BLAS: High-performance model implementations and performance evaluation benchmark, Tech. Rep. UMINF 95-18, Department of Computing Science, Umeå University, 1995.
Submitted to ACM Trans. Math. Softw.

73

B. KÅGSTR¨OM AND P. POROMAA, Computing eigenspaces with specified eigenvalues of a regular matrix pair (A,B) and condition estimation: Theory, algorithms and software, Tech. Rep. UMINF 94.04, Department of Computing Science, Umeå University, 1994.

74

B. KÅGSTRÖM AND P. POROMAA, LAPACK-style algorithms and software for solving the generalized Sylvester equation and estimating the separation between regular matrix pairs, ACM Trans. Math. Softw., 22 (1996), pp. 78-103.

75

B. KÅGSTRÖM AND L. WESTIN, Generalized schur methods with condition estimators for solving the generalized Sylvester equation, IEEE Trans. Autom. Contr., 34 (1989), pp. 745-751.

76

T. KATO, Perturbation Theory for Linear Operators, Springer-Verlag, Berlin, 2 ed., 1980.

77

L. KAUFMAN, Banded eigenvalue solvers on vector machines, ACM Trans. Math. Softw., 10 (1984), pp. 73-86.

78

C. L. LAWSON, R. J. HANSON, D. KINCAID, AND F. T. KROGH, Basic linear algebra subprograms for Fortran usage, ACM Trans. Math. Soft., 5 (1979), pp. 308-323.

79

R. LEHOUCQ, The computation of elementary unitary matrices, Computer Science Dept. Technical Report CS-94-233, University of Tennessee, Knoxville, TN, 1994.
(Also LAPACK Working Note 72).

80

C. PAIGE, Computer solution and perturbation analysis of generalized linear least squares problems, Math. of Comput., 33 (1979), pp. 171-183.

81

C. PAIGE, Fast numerically stable computations for generalized linear least squares problems controllability, SIAM J. Num. Anal., 16 (1979), pp. 165-179.

82

C. PAIGE, A note on a result of sun ji-guang: sensitivity of the cs and gsv decomposition, SIAM J. Num. Anal., 21 (1984), pp. 186-191.

83

C. PAIGE, Computing the generalized singular value decomposition, SIAM J. Sci. Stat., 7 (1986), pp. 1126-1146.

84

C. PAIGE, Some aspects of generalized QR factorization, in Reliable Numerical Computations, M. Cox and S. Hammarling, eds., Clarendon Press, 1990.

85

B. PARLETT, The Symmetric Eigenvalue Problem, Prentice-Hall, Englewood Cliffs, NJ, 1980.

86

B. N. PARLETT AND I. S. DHILLON, Relatively robust representation of symmetric tridiagonals, June 1999.
to appear.

87

B. N. PARLETT AND O. A. MARQUES, An implementation of the dqds algorithm (positive case), June 1999.
to appear.

88

E. POLLICINI, A. A., Using Toolpack Software Tools, 1989.

89

J. RUTTER, A serial implementation of cuppen's divide and conquer algorithm for the symmetric tridiagonal eigenproblem, Computer Science Division Report UCB/CSD 94/799, University of California, Berkeley, Berkeley, CA, 1994.
(Also LAPACK Working Note 69).

90

R. SCHREIBER AND C. F. VAN LOAN, A storage efficient WY representation for products of Householder transformations, SIAM J. Sci. Stat. Comput., 10 (1989), pp. 53-57.

91

I. SLAPNISCAR, Accurate symmetric eigenreduction by a Jacobi method, PhD thesis, Fernuniversität - Hagen, Hagen, Germany, 1992.

92

B. T. SMITH, J. M. BOYLE, J. J. DONGARRA, B. S. GARBOW, Y. IKEBE, V. C. KLEMA, AND C. B. MOLER, Matrix Eigensystem Routines - EISPACK Guide, vol. 6 of Lecture Notes in Computer Science, Springer-Verlag, Berlin, 1976.

93

G. W. STEWART, On the sensitivity of the eigenvalue problem 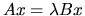$Ax = \lambda Bx$, SIAM J. Num. Anal., 9 (1972), pp. 669-686.

94

G. W. STEWART, Error and perturbation bounds for subspaces associated with certain eigenvalue problems, SIAM Review, 15 (1973), pp. 727-764.

95

G. W. STEWART AND J.-G. SUN, Matrix Perturbation Theory, Academic Press, New York, 1990.

96

J. G. SUN, Perturbation analysis for the generalized singular value problem, SIAM J. Num. Anal., 20 (1983), pp. 611-625.

97

P. VAN DOOREN, The computation of Kronecker's canonical form of a singular pencil, Lin. Alg. Appl., 27 (1979), pp. 103-141.

98

J. VARAH, On the separation of two matrices, SIAM J. Numer. Anal., 16 (1979), pp. 216-222.

99

K. VESELI´C AND I. SLAPNISCAR, Floating-point perturbations of Hermitian matrices, Linear Algebra and Appl., 195 (1993), pp. 81-116.

100

R. C. WARD, Balancing the generalized eigenvalue problem, SIAM J. Sci. Stat. Comput., 2 (1981), pp. 141-152.

101

D. WATKINS AND L. ELSNER, Convergence of algorithms of decomposition type for the eigenvalue problem, Linear Algebra Appl., 143 (1991), pp. 19-47.

102

R. C. WHALEY AND J. DONGARRA, Automatically Tuned Linear Algebra Software.
http://www.supercomp.org/sc98/TechPapers/sc98_FullAbstracts/Whaley814/INDEX .HTM, 1998.
Winner, best paper in the systems category, SC98: High Performance Networking and Computing.

103

J. H. WILKINSON, The Algebraic Eigenvalue Problem, Oxford University Press, Oxford, UK, 1965.

104

J. H. WILKINSON, Some recent advances in numerical linear algebra, in The State of the Art in Numerical Analysis, D. A. H. Jacobs, ed., Academic Press, New York, 1977.

105

J. H. WILKINSON, Kronecker's canonical form and the QZ algorithm, Lin. Alg. Appl., 28 (1979), pp. 285-303.

106

J. H. WILKINSON AND C. REINSCH, eds., Handbook for Automatic Computation, vol 2.: Linear Algebra, Springer-Verlag, Heidelberg, 1971.