Subsections
Οι τεχνικές αριθμητικής επίλυσης της εξίσωσης του Schrödinger
είναι πολλές, και φυσικά δεν μπορούν να αναπτυχθούν εδώ. Πέρα από τη
βιβλιογραφία που δίνουμε σ' αυτό το κεφάλαιο, καταγράφουμε επίσης
μερικές από τις
βασικές εξισώσεις και Χαμιλτονιανές που χρησιμοποιούμε στη Μοριακή Κβαντική
Μηχανική.
Στη Χημική Δυναμική εργαζόμαστε συνήθως με γενικευμένα συστήματα
συντεταγμένων. Για παράδειγμα, τα τριατομικά μόρια έχουν τις παρακάτω
Χαμιλτονιανές.
4.1.1 Συντεταγμένες Σθένους
Αγνοώντας την κίνηση του κέντρου μάζας και τις περιστροφές του μορίου, η
Χαμιλτονιανή σε συντεταγμένες σθένους (τα δύο μήκη δεσμών r1, r2,
και την μεταξύ τους γωνία 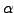 , Σχήμα 2.2) γράφεται:
, Σχήμα 2.2) γράφεται:
| Hnuc |
= |
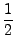 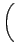 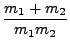 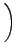 p12 + p12 + 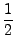  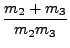 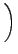 p22 + p22 + 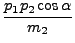 + + |
|
| |
|
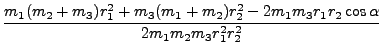 p p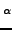 2 - 2 - |
|
| |
|
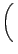 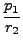 + + 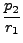 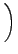 p p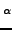 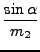 + U(r1, r2, + U(r1, r2,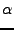 ). ). |
(4.1) |
p1, p2, p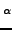 είναι οι συζυγείς ορμές των συντεταγμένων
r1, r2,
είναι οι συζυγείς ορμές των συντεταγμένων
r1, r2,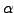 .
.
4.1.2 Συντεταγμένες Σκέδασης
Σε προβλήματα σκέδασης ενός ατόμου από ένα διατομικό μόριο ή στη μελέτη των
δονήσεων ενός εύκαμπτου τριατομικού μορίου, όπως τα συστήματα van der Waals,
χρησιμοποιούμε τις συντεταγμένες σκέδασης (Σχήμα 2.2), και η Χαμιλτονιανή παίρνει
τη μορφή:
Hnuc = 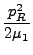 + + 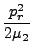 + + 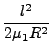 + + 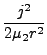 + U(r, R, + U(r, R,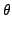 ). ). |
(4.2) |
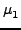 και
και 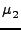 είναι οι ανηγμένες μάζες:
είναι οι ανηγμένες μάζες:
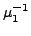 = m1-1 + (m2 + m3)-1
= m1-1 + (m2 + m3)-1
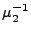 = m2-1 + m3-1.
= m2-1 + m3-1.
l είναι η στροφορμή του ατόμου A ως προς το κέντρο μάζας του μορίου BC, και j
η στροφορμή του διατομικού μορίου BC. pr και pR συμβολίζουν τις
συζυγείς ορμές των συντεταγμένων r και R αντιστοίχως.
Από την κλασική Χαμιλτονιανή περνούμε στην κβαντική Χαμιλτονιανή με τη
γνωστή
διαδικασία που περιγράφεται στο βιβλίο των Wilson-Decious-Cross[35].
Για παράδειγμα, η Χαμιλτονιανή 4.2 για ένα μη περιστρεφόμενο μόριο
μετασχηματίζεται στον τελεστή:
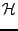 nuc nuc |
= |
- 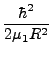 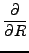 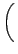 R2 R2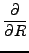 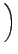 - - 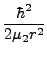 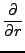 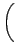 r2 r2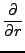 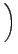 - - |
|
| |
|
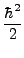 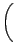 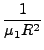 + + 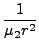 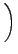 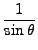 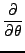 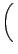 sin sin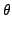 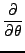 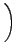 . . |
(4.3) |
Η εξίσωση του Schrödinger,
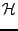 nuc nuc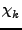 = = 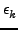 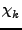 , k = 0, 1,..., , k = 0, 1,..., |
(4.4) |
επιλύεται συνήθως με τη μέθοδο των μεταβολών, αφού πρώτα επιλέξουμε
μία κατάλληλη βάση ανάπτυξης των κυματοσυναρτήσεων. Εφόσον βεβαιωθούμε
για τη σύγκλιση των υπολογισμών μας, οι ιδιοτιμές είναι ανεξάρτητες των
συντεταγμένων και της βάσης.
Η χρονική εξέλιξη ενός μορίου μελετάται άμεσα λύνοντας την χρονική
εξίσωση του Schrödinger [26]:
Τελευταία έχουν αναπτυχθεί αλγόριθμοι για την αριθμητική επίλυση της
Εξίσωσης 4.5, και με τους σύγχρονους Η/Υ μπορούμε να βρούμε τις λύσεις
αυτές για μεγάλα χρονικά διαστήματα[36].
Figure:
Στιγμιότυπα από την
χρονική εξέλιξη ενός κυματοπακέτου Gaussian.
|
|
Η Εξίσωση 4.5 είναι μία εξίσωση αρχικών τιμών.
Συνήθως η αρχική κυματοσυνάρτηση είναι μια Gaussian ή μια συνάρτηση που
περιγράφει την αρχική κατάσταση του μορίου. Το
Σχήμα 4.1 παρουσιάζει τη χρονική εξέλιξη ενός κυματοπακέτου Gaussian.
Έχοντας τη χρονική λύση
της εξίσωσης του Schrödinger μπορούμε να υπολογίσουμε την ενεργό
διατομή σε προβλήματα κρούσεων, φάσματα, αλλά και κάθε άλλη δυναμική
ποσότητα (Σχήμα 4.2).
Figure:
Συνάρτηση αυτοσυσχέτισης υπολογισμένη με την
επίλυση της χρονοεξηρτημένης εξίσωσης του Schrödinger.
|
|
Farantos Stavros
2011-05-30
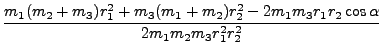 p
p
![\includegraphics[scale=0.6]{figures/fig4_2.eps}](img269.png)