Subsections
Η Χημική Κινητική είναι ο τομέας που ασχολείται με τη μέτρηση των
ταχυτήτων των χημικών αντιδράσεων σε μακροσκοπικό επίπεδο.
Για παράδειγμα, η ταχύτητα της αντίδρασης
A + BCD 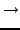 AB + CD,
AB + CD,
περιγράφεται από την εμπειρική εξίσωση:
![$\displaystyle {\frac{{d[A]}}{{dt}}}$](img81.png) = - k'[A][BCD]. = - k'[A][BCD]. |
(3.1) |
k' είναι η σταθερά ταχύτητας, και συνήθως εξαρτάται από την
θερμοκρασία, ενώ τα [A], και [BCD] συμβολίζουν τις συγκεντρώσεις των
αντιδρώντων.
Προϋπόθεση για μια μικροσκοπική περιγραφή της αντίδρασης 3.1
είναι ο υπολογισμός της ενεργούς διατομής (cross section),
ποσότητας που δίνει την πιθανότητα κρούσεως των αντιδρώντων
μορίων, A και BCD, για να δώσουν τα προϊόντα AB και CD.
Επιπλέον, ενδιαφερόμαστε
να υπολογίσουμε την ενεργό διατομή σαν συνάρτηση της αρχικής ενέργειας
κρούσεως και των κβαντικών καταστάσεων των αντιδρώντων και προϊόντων μορίων.
Στην επόμενη παράγραφο περιγράφουμε τη μέθοδο των κλασικών τροχιών για
την αντίδραση 3.1. Αν και πραγματευόμαστε ένα ειδικό παράδειγμα,
η γενίκευση της μεθόδου σε άλλες στοιχειώδεις μοριακές διεργασίες μπορεί
εύκολα να γίνει και θεωρητικά αλλά και υπολογιστικά.
3.1 Η μέθοδος των κλασικών τροχιών
Σε ένα σταθερό στον χώρο σύστημα συντεταγμένων, το τετρατομικό σύστημα
ABCD περιγράφεται με 12 καρτεσιανές συντεταγμένες. Η χρονική εξέλιξη του
συστήματος δίνεται από τις εξισώσεις Hamilton:
i = 1,...12.
Τα qi συμβολίζουν τις καρτεσιανές συντεταγμένες, και τα pi τις
αντίστοιχες συζυγείς ορμές. Η κλασική χαμιλτονιανή H,
περιλαμβάνει την κινητική ενέργεια και το δυναμικό U που είναι συνάρτηση
των αποστάσεων μεταξύ των ατόμων A, B, C και D. Τα mi
συμβολίζουν τις μάζες των ατόμων.
Μπορεί κανείς να δείξει με Ημικλασική Μηχανική[16], ότι η ενεργός
διατομή υπολογίζεται από το πολλαπλό ολοκλήρωμα,
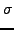 (Vr) (Vr) |
= |
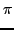 bmax2 bmax2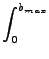 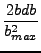 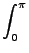 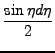 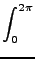 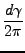 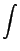 FErot(J, m)dJdm x FErot(J, m)dJdm x |
|
| |
|
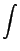 Fv1v2v3(R4, R5, R6)dv1dv2dv3 Fv1v2v3(R4, R5, R6)dv1dv2dv3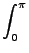 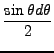 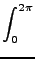 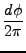 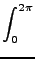 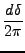 x x |
|
| |
|
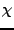 (b, (b,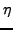 , ,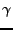 , J, m, v1, v2, v3, R4, R5, R6, , J, m, v1, v2, v3, R4, R5, R6,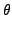 , ,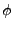 , ,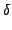 , Vr, Rs). , Vr, Rs). |
(3.3) |
Οι μεταβλητές συμβολίζουν:
| b | : | παράμετρος κρούσεως |
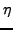 , ,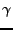 | : | σφαιρικές πολικές συντεταγμένες που καθορίζουν τη διεύθυνση |
| | : | της στροφορμής του τριατομικού μορίου |
| Erot | : | περιστροφική ενέργεια η οποία εξαρτάται από τον κβαντικό αριθμό |
| | : | της ολικής στροφορμής J, και την προβολή της στον άξονα
z, m |
| v1, v2, v3 | : | δονητικοί κβαντικοί αριθμοί που περιγράφουν τις τρεις κανονικές |
| | : | δονήσεις ή τις τρεις τοπικές δονήσεις των δεσμών, |
| | : |  |
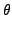 , ,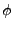 , ,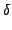 | : | οι τρεις γωνίες Euler που καθορίζουν τον προσανατολισμό του |
| | : | μορίου στο σταθερό στον χώρο σύστημα συντεταγμένων |
| Vr | : | η σχετική ταχύτητα του ατόμου A ως προς το κέντρο μάζας
του |
| | : | BCD |
| I>Rs | : | ο αρχικός διαχωρισμός του A από το BCD. Στην απόσταση αυτή |
| | : | το δυναμικό αλληλεπίδρασης είναι πρακτικά μηδέν |
| FErot | : | συνάρτηση κατανομής των περιστροφικών καταστάσεων του μορίου |
| Fv1, v2, v3 | : | συνάρτηση κατανομής των δονητικών καταστάσεων του μορίου |
Η χαρακτηριστική συνάρτηση 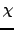 παίρνει τιμές 1 ή 0. Εάν η κλασική
τροχιά με αρχικές συνθήκες που υπολογίζονται από τις παραπάνω μεταβλητές οδηγεί στα
προϊόντα της αντίδρασης, και μάλιστα στις συγκεκριμένες καταστάσεις που μας
ενδιαφέρουν, η τιμή της συνάρτησης
παίρνει τιμές 1 ή 0. Εάν η κλασική
τροχιά με αρχικές συνθήκες που υπολογίζονται από τις παραπάνω μεταβλητές οδηγεί στα
προϊόντα της αντίδρασης, και μάλιστα στις συγκεκριμένες καταστάσεις που μας
ενδιαφέρουν, η τιμή της συνάρτησης 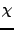 είναι 1, αλλιώς θεωρείται μηδέν.
είναι 1, αλλιώς θεωρείται μηδέν.
Εάν μας ενδιαφέρει να υπολογίσουμε τις ενεργές διατομές για καθορισμένες
κβαντικές καταστάσεις των αντιδρώντων, τότε
οι συναρτήσεις κατανομής των περιστροφικών και δονητικών καταστάσεων είναι:
FErot = 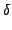 (Erot - EJm), (Erot - EJm), |
(3.4) |
Fv1, v2, v3 = 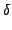 (Ev - Ev1, v2, v3). (Ev - Ev1, v2, v3). |
(3.5) |
Το ολοκλήρωμα 3.3 ανάγεται στο
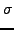 (v1, v2, v3, J, m, Vr) = (v1, v2, v3, J, m, Vr) = 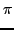 bmax2 bmax2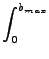 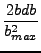 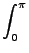 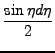 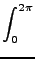 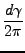 x x |
|
|
|
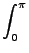 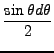 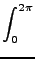 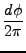 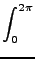 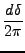 x x |
|
|
|
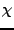 (b, (b,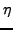 , ,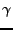 , J, m, v1, v2, v3, R4, R5, R6, , J, m, v1, v2, v3, R4, R5, R6,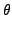 , ,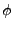 , ,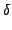 , Vr, Rs). , Vr, Rs). |
|
|
(3.6) |
Η μακροσκοπική ταχύτητα αντίδρασης βρίσκεται παίρνοντας τον μέσο
όρο της ενεργούς διατομής ως προς τη σχετική ταχύτητα, των οποίων η κατανομή
θεωρείται ότι είναι τύπου Boltzmann:
| k(v1, v2, v3, J, m, T) = |
|
|
|
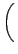 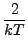 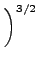 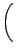 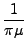 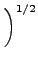 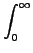 Er Er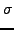 (v1, v2, v3, J, m, Er) x (v1, v2, v3, J, m, Er) x |
|
|
|
exp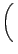 - - 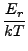 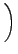 dEr. dEr. |
|
|
(3.7) |
Το 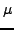 συμβολίζει την ανηγμένη μάζα του A ως προς το BCD,
και Er τη μεταφορική ενέργεια.
συμβολίζει την ανηγμένη μάζα του A ως προς το BCD,
και Er τη μεταφορική ενέργεια.
Er = 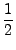 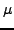 Vr2. Vr2. |
(3.8) |
Εάν θέλουμε να υπολογίσουμε την ταχύτητα αντίδρασης ως μέσο όρο των
δονητικών και περιστροφικών καταστάσεων των αντιδρώντων μορίων,
υποθέτοντας μία κατανομή Boltzmann για τις καταστάσεις,
υπολογίζουμε τα ολοκληρώματα,
k(T) = 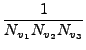 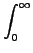 k(v1, v2, v3, J, m, T) k(v1, v2, v3, J, m, T) |
|
|
|
exp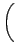 - - 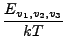 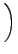 exp exp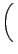 - - 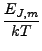 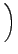 dv1dv2dv3dJdm. dv1dv2dv3dJdm. |
|
|
(3.9) |
Nvi είναι οι συναρτήσεις κατανομής (partition function) των αντιδρώντων μορίων.
Το ολοκλήρωμα 3.6 υπολογίζεται με τη μέθοδο Monte Carlo[27].
Ορίζοντας τη συνάρτηση βάρους,
η Eξίσωση 3.6 παίρνει τη μορφή
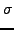 (v1, v2, v3, J, m, Vr) = (v1, v2, v3, J, m, Vr) = 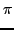 bmax2 bmax2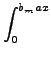 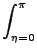 |
|
|
|
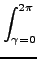 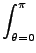 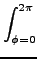 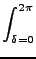 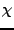 wdbd wdbd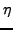 d d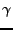 d d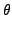 d d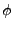 d d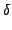 . . |
|
|
(3.11) |
Για να εφαρμόσουμε την τεχνική Monte Carlo αναζητούμε ένα μετασχηματισμό
(b,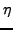 , ,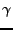 , ,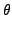 , ,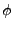 , ,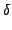 ) ) 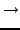 ( (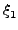 , ,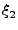 , ,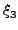 , ,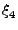 , ,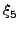 , ,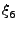 ), ), |
(3.12) |
όπου οι 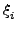 είναι ομοιόμορφοι ψευδοτυχαίοι αριθμοί, και η Jacobian του
μετασχηματισμού ίση με w-1.
Το ολοκλήρωμα 3.11 τότε γίνεται:
είναι ομοιόμορφοι ψευδοτυχαίοι αριθμοί, και η Jacobian του
μετασχηματισμού ίση με w-1.
Το ολοκλήρωμα 3.11 τότε γίνεται:
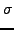 (v1, v2, v3, J, m, Vr) = (v1, v2, v3, J, m, Vr) = 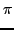 bmax2 bmax2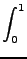 ... ... 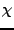 (v1, v2, v3, J, m, Vr, (v1, v2, v3, J, m, Vr,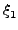 ,..., ,...,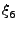 )d )d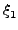 ...d ...d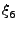 . . |
(3.13) |
Αριθμητικά το παραπάνω ολοκλήρωμα υπολογίζεται από τον τύπo:
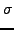 (v1, v2, v3, J, m, Vr) = (v1, v2, v3, J, m, Vr) = |
|
|
|
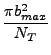 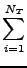 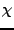 (v1, v2, v3, J, m, Vr, (v1, v2, v3, J, m, Vr,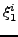 ,..., ,...,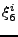 ) = ) = |
|
|
|
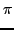 bmax2 bmax2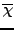 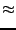 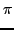 bmax2 bmax2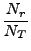 , , |
|
|
(3.14) |
όπου Nr ο αριθμός των τροχιών που οδηγούν σε αντίδραση, NT ο ολικός
αριθμός των τροχιών και
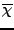 = Nr/NT.
= Nr/NT.
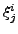 είναι ψευδοτυχαίοι αριθμοί, που χρησιμοποιούνται
για την επιλογή αρχικών συνθηκών της i-τής τροχιάς.
είναι ψευδοτυχαίοι αριθμοί, που χρησιμοποιούνται
για την επιλογή αρχικών συνθηκών της i-τής τροχιάς.
Ο μετασχηματισμός w, από τις δυναμικές μεταβλητές στους ψευδοτυχαίους
αριθμούς, βρίσκεται από τη σχέση:
όπου 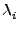 είναι η συνάρτηση πυκνότητας πιθανότητας της μεταβλητής y,
και
είναι η συνάρτηση πυκνότητας πιθανότητας της μεταβλητής y,
και 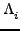 ο συντελεστής κανονικοποίησης της
ο συντελεστής κανονικοποίησης της 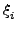 . Σαν παράδειγμα,
ας υπολογίσουμε τον μετασχηματισμό για την παράμετρο κρούσεως, b:
. Σαν παράδειγμα,
ας υπολογίσουμε τον μετασχηματισμό για την παράμετρο κρούσεως, b:
b = bmax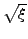 1. 1. |
(3.16) |
Ομοίως βρίσκουμε:
cos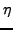 |
= |
1 - 2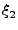 |
|
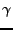 |
= |
2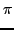 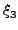 |
|
cos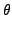 |
= |
1 - 2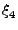 |
|
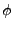 |
= |
2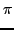 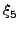 |
|
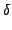 |
= |
2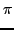 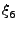 . . |
(3.17) |
Τέσσερις ακόμη ψευδοτυχαίοι αριθμοί πρέπει να επιλεγούν για τον πλήρη
ορισμό των αρχικών συνθηκών: ο 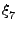 , ο οποίος σχετίζεται
με τη σχετική απόσταση των αντιδρώντων μορίων Rs, και οι
, ο οποίος σχετίζεται
με τη σχετική απόσταση των αντιδρώντων μορίων Rs, και οι
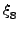 ,
,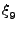 ,
,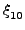 που αντιστοιχούν στις φάσεις των ταλαντώσεων του τριατομικού μορίου. Αυτό
θα το εξηγήσουμε καλύτερα στην επόμενη παράγραφο.
Μία εκτίμηση του σφάλματος στην Monte Carlo ολοκλήρωση βρίσκεται από τη
σχέση:
που αντιστοιχούν στις φάσεις των ταλαντώσεων του τριατομικού μορίου. Αυτό
θα το εξηγήσουμε καλύτερα στην επόμενη παράγραφο.
Μία εκτίμηση του σφάλματος στην Monte Carlo ολοκλήρωση βρίσκεται από τη
σχέση:
s2 = 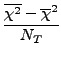 . . |
(3.18) |
Επειδή
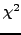 =
= 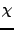 , η παραπάνω εξίσωση πολλαπλασιάζοντάς την με
(
, η παραπάνω εξίσωση πολλαπλασιάζοντάς την με
(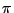 bmax2)2
και λαμβάνοντας υπ' όψιν την Εξίσωση 3.14 γίνεται:
bmax2)2
και λαμβάνοντας υπ' όψιν την Εξίσωση 3.14 γίνεται:
d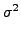 |
= |
(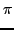 bmax2)2 bmax2)2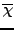 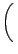 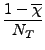 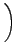 |
|
| |
= |
(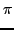 bmax2)2 bmax2)2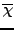 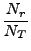 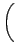 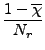 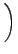 |
|
| |
= |
(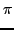 bmax2)2 bmax2)2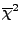 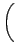 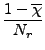 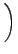 , , |
(3.19) |
δηλαδή
Συνοψίζοντας, η μέθοδος των κλασικών τροχιών περιλαμβάνει τα εξής τρία
βήματα:
- Επιλογή αρχικών συνθηκών για τις τροχιές, κατά τέτοιο τρόπο ώστε να γίνεται προσομοίωση των αρχικών κβαντικών καταστάσεων των αντιδρώντων. Στην επόμενη
παράγραφο περιγράφουμε πώς επιτυγχάνεται αυτό με την ημικλασική κβάντωση των
κατάλληλων τροχιών.
- Ολοκλήρωση των τροχιών.
- Ανάλυση των κλασικών τροχιών μετά το πέρας της ολοκλήρωσης για την εύρεση
της τελικής κατάστασης των προϊόντων, αλλά και των αντιδρώντων μορίων εάν
οι κρούσεις είναι μη-ελαστικές.
Σαν ένα παράδειγμα εφαρμογής της μεθόδου των κλασικών τροχιών στον Πίνακα
3.1 συγκρίνουμε τη σταθερά ταχύτητας της αντίδρασης
Cl + O3 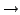 ClO + O2, που υπολογίσθηκε με το δυναμικό της
Παραγράφου 2.3, με τις αντίστοιχες πειραματικές τιμές[25].
ClO + O2, που υπολογίσθηκε με το δυναμικό της
Παραγράφου 2.3, με τις αντίστοιχες πειραματικές τιμές[25].
|
k' x 1011 | |
|
Τ/K |
cm3molecule-1s-1 | Πειραματικές τιμές |
|
200 | 1.00 | 1.00 |
|
220 | 1.07 | 1.10 |
|
300 | 1.34 | 1.36 |
|
600 | 2.11 | 2.58 |
3.2 H Κβαντική συνθήκη των Einstein-Brellouin-Keller
Η αντιστοιχία κλασικών τροχιών και κβαντικών καταστάσεων επιτυγχάνεται
στα πλαίσια της ημικλασικής προσέγγισης.
Η ημικλασική συνθήκη κβάντωσης για συστήματα με ένα βαθμό ελευθερίας είναι
η γνωστή σχέση των Bohr-Sommerfeld[28]:
Η γενίκευση αυτής της συνθήκης για μη-διαχωρίσιμα πολυδιάστατα συστήματα
με N βαθμούς ελευθερίας δόθηκε από τους
Einstein-Brillouin-Keller[29] και αναφέρεται ως συνθήκη-EBK:
Jk = 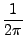 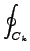  = = 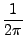 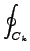 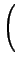 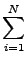 pidqi pidqi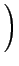 = (nk + = (nk + 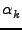 /4) /4)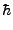 . . |
(3.22) |
Jk,
k = 1, 2,..., N, είναι οι μεταβλητές δράσης,
nk κβαντικοί αριθμοί, και 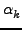 οι δείκτες Maslov. Ένας μη
αυστηρός ορισμός του δείκτη Maslov είναι ως ο αριθμός των σημείων καμπής της
τροχιάς: για ταλαντώσεις
οι δείκτες Maslov. Ένας μη
αυστηρός ορισμός του δείκτη Maslov είναι ως ο αριθμός των σημείων καμπής της
τροχιάς: για ταλαντώσεις
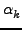 = 2, και για περιστροφές
= 2, και για περιστροφές
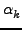 = 0.
Τα Ck συμβολίζουν τοπολογικά ανεξάρτητες καμπύλες ως προς τις οποίες
ολοκληρώνουμε για την εύρεση των μεταβλητών δράσης Jk. Για συστήματα δύο
βαθμών ελευθερίας οι καμπύλες αυτές δείχνονται στο Σχήμα 3.1.
Σύμφωνα λοιπόν με τις Εξισώσεις 3.22, πρέπει να εντοπίσουμε εκείνες τις
ημιπεριοδικές τροχιές, των οποίων οι μεταβλητές δράσης ικανοποιούν τη
συνθήκη ημικλασικής κβάντωσης. Οι ενέργειες αυτών των τροχιών αντιστοιχούν
στις ιδιοτιμές του συστήματος.
= 0.
Τα Ck συμβολίζουν τοπολογικά ανεξάρτητες καμπύλες ως προς τις οποίες
ολοκληρώνουμε για την εύρεση των μεταβλητών δράσης Jk. Για συστήματα δύο
βαθμών ελευθερίας οι καμπύλες αυτές δείχνονται στο Σχήμα 3.1.
Σύμφωνα λοιπόν με τις Εξισώσεις 3.22, πρέπει να εντοπίσουμε εκείνες τις
ημιπεριοδικές τροχιές, των οποίων οι μεταβλητές δράσης ικανοποιούν τη
συνθήκη ημικλασικής κβάντωσης. Οι ενέργειες αυτών των τροχιών αντιστοιχούν
στις ιδιοτιμές του συστήματος.
Figure:
Η μορφή ενός διδιάστατου torus, όπου
φαίνονται οι μη-αναγωγήσιμες καμπύλες C1, και C2.
|
|
Στην περίπτωση του αρμονικού ταλαντωτή οι μεταβλητές δράσης-γωνίες,
(Jk,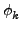 ),
μπορούν να υπολογισθούν αναλυτικά. Γενικά, εάν αναπτύξουμε την ΔΕΕ σε μία
σειρά Taylor και μέχρι τους όρους δευτέρου βαθμού, τότε υπάρχει
μετασχηματισμός τέτοιος ώστε η Χαμιλτονιανή ενός τριατομικού μορίου για
παράδειγμα, γράφεται στη μορφή:
),
μπορούν να υπολογισθούν αναλυτικά. Γενικά, εάν αναπτύξουμε την ΔΕΕ σε μία
σειρά Taylor και μέχρι τους όρους δευτέρου βαθμού, τότε υπάρχει
μετασχηματισμός τέτοιος ώστε η Χαμιλτονιανή ενός τριατομικού μορίου για
παράδειγμα, γράφεται στη μορφή:
Hhar = 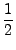 (P12 + (P12 + 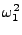 Q12) + Q12) + 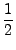 (P22 + (P22 + 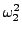 Q22) + Q22) + 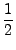 (P32 + (P32 + 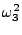 Q32). Q32). |
(3.23) |
Qi είναι οι κανονικές συντεταγμένες του μορίου, Pi οι αντίστοιχες
συζυγείς ορμές, και 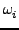 οι θεμελιώδεις συχνότητες. Ο μετασχηματισμός
στις μεταβλητές δράσης-γωνίες, (J,
οι θεμελιώδεις συχνότητες. Ο μετασχηματισμός
στις μεταβλητές δράσης-γωνίες, (J,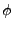 ), δίνεται από τις εξισώσεις:
), δίνεται από τις εξισώσεις:
| Qi |
= |
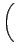 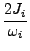 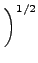 cos cos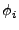 |
(3.24) |
| Pi |
= |
- (2Ji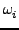 )1/2sin )1/2sin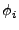 . . |
(3.25) |
H Χαμιλτονιανή τότε παίρνει τη μορφή:
Hhar = J1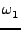 + J2 + J2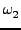 + J3 + J3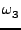 . . |
(3.26) |
Οι λύσεις των εξισώσεων Hamilton στις μεταβλητές δράσης-γωνίες είναι:
| Ji |
= |
σταθερά |
(3.27) |
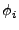 |
= |
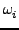 t + t + 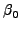 , , |
(3.28) |
όπου 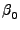 η αρχική φάση. Οι Εξισώσεις 3.24 είναι αυτές ενός
torus
και οι τροχιές που καλύπτουν την επιφάνεια ενός torus ονομάζονται
ημιπεριοδικές ή κανονικές τροχιές.
η αρχική φάση. Οι Εξισώσεις 3.24 είναι αυτές ενός
torus
και οι τροχιές που καλύπτουν την επιφάνεια ενός torus ονομάζονται
ημιπεριοδικές ή κανονικές τροχιές.
Ένα από τα πιο σημαντικά θεωρήματα της Κλασικής Μηχανικής είναι το θεώρημα
των Kolmogorov-Arlnod-Moser[30], που αποδεικνύει ότι τα
tori δεν
καταστρέφονται όταν εισάγουμε στην Χαμιλτονιανή μικρούς μη-αρμονικούς όρους.
Έτσι, αναμένουμε να έχουμε ημιπεριοδικές τροχιές και για μη-αρμονικά
δυναμικά.
Για μη-αρμονικά μη-διαχωρίσιμα συστήματα ο υπολογισμός των μεταβλητών
δράσης, και ακολούθως η κβάντωσή τους, γίνεται αριθμητικά. Έχουν προταθεί
διάφορες τεχνικές, η πιο πετυχημένη από τις οποίες είναι η ανάπτυξη των
συντεταγμένων και των ορμών σε σειρές Fourier.
q(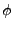 , J) = , J) = 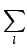 ql(J)exp(il ql(J)exp(il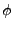 ) ) |
|
|
(3.29) |
p(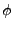 , J) = , J) = 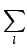 pl(J)exp(il pl(J)exp(il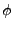 ). ). |
|
|
(3.30) |
Figure:
Ένα τυπικό φάσμα ημιπεριοδικής τροχιάς.
|
|
Tο Σχήμα 3.2 δείχνει την ανάλυση Fourier μιας ημιπεριοδικής τροχιάς. Ο
άξονας των Χ απεικονίζει τη συχνότητα και ο άξονας των Υ το τετράγωνο των
συντελεστών Fourier. Οι κορυφές αντιστοιχούν στις θεμελιώδεις συχνότητες
και σε συνδυασμούς τους.
Με τη μέθοδο των μεταβολών[29] μπορούμε να υπολογίσουμε και τις
μεταβλητές δράσης που αντιστοιχούν στις συνθήκες κβάντωσης. Στην πράξη αυτό
δεν είναι εύκολο, και γι' αυτό συχνά χρησιμοποιούμε την αρμονική
προσέγγιση για την εύρεση αρχικών συνθηκών στη μέθοδο των κλασικών
τροχιών.
3.3 H Κβαντική συνθήκη του Gutzwiller
Ημικλασική Μηχανική σημαίνει τον ορισμό μιας αντιστοιχίας κλασικών
αντικειμένων όπως τα tori με τις κβαντικές κυματοσυναρτήσεις.
Tori όμως ή
ισοδύναμα ημιπεριοδικές τροχιές υπάρχουν για χαμηλές διεγέρσεις των
μορίων όπου η απόκλιση από την αρμονική προσέγγιση είναι μικρή.
Στα διεγερμένα μόρια ο φασικός χώρος καταλαμβάνεται από χαοτικές τροχιές
και αμέσως μπαίνει το ερώτημα ποιες τροχιές αντιστοιχούν στις κβαντικές
κυματοσυναρτήσεις σε μια ημικλασική θεωρία.
Μία απάντηση έδωσε ο Gutzwiller όταν προσπάθησε να υπολογίσει τη
κβαντική πυκνότητα καταστάσεων στην ημικλασική προσέγγιση [31].
Η πυκνότητα καταστάσεων στην ενέργεια Ε, D(E), ορίζεται:
D(E) = 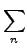 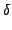 (E - En) = Dav(E) + N(E), (E - En) = Dav(E) + N(E), |
(3.31) |
όπου N(E) είναι οι μεταβολές της πυκνότητας από τη μέση τιμή Dav(E).
Τα αθροίσματα στην παραπάνω εξίσωση είναι πάνω από όλες τις πιθανές
περιοδικές τροχιές με περίοδο Tpo και δράση Spo. Mpoj
συμβολίζει τον πίνακα ευστάθειας ο οποίος περιγράφει τη συμπεριφορά
των γειτονικών τροχιών της περιοδικής τροχιάς. Εάν δηλαδή παραμένουν κοντά
στη περιοδική τροχιά με την πάροδο του χρόνου ή αποκλίνουν εκθετικά
από αυτή.
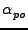 είναι ο δείκτης Maslov.
είναι ο δείκτης Maslov.
Οι παραπάνω ποσότητες υπολογίζονται κάθε φορά που εντοπίζουμε τις
περιοδικές λύσεις των εξισώσεων Hamilton. Όπως θα δούμε στο επόμενο
κεφάλαιο οι περιοδικές τροχιές σε ένα σύστημα όχι μόνο επιτρέπουν την
εισαγωγή ενός τρόπου ημικλασικής κβάντωσης σε καταστάσεις χαοτικής
συμπεριφοράς αλλά και στον ορισμό μιας αντιστοιχίας με τις
κυματοσυναρτήσεις. Σε συστήματα όπου αναμένεται η Ημικλασική Μηχανική
να δίνει μια καλή προσέγγιση της συμπεριφοράς τους, βρίσκουμε
τις ιδιοσυναρτήσεις να χαράσσονται από συγκεκριμένες περιοδικές
τροχιές [32]. Η παρατήρηση αυτή μας έχει επιτρέψει να αναπτύξουμε
τη Μέθοδο των Περιοδικών Τροχιών για τη διερεύνηση εντοπισμένων
δονητικών κυματοσυναρτήσεων στα μόρια και επομένως την κατανόηση της
φασματοσκοπίας υψηλά διεγερμένων μορίων (δες παράγραφο 5.3).
Η εύρεση περιοδικών λύσεων σε προβλήματα αρχικών τιμών που περιγράφονται
με διαφορικές εξισώσεις, όπως αυτές των εξισώσεων Hamilton, απασχολεί
τους ερευνητές από την εποχή του Poincaré. Το πρόβλημα γίνεται ακόμη
πιο οξύ για τα μόρια εάν λάβουμε υπ' όψιν μας τις πολλές διαστάσεις
αυτών των συστημάτων. Κατά τη γνώμη μας η μέθοδος των Πολλαπλών
Εκτοξεύσεων [33] είναι η πλέον κατάλληλη για πολυδιάστατα
συστήματα με αστάθεια και μεγάλες περιόδους. Ο συνδυασμός του εντοπισμού
των θεμελιωδών οικογενειών των περιοδικών τροχιών με την κατασκευή
διαγραμμάτων συνέχειας/διακλαδώσεων μας έχει επιτρέψει να
μελετήσουμε τη δομή του φασικού χώρου πολλών μορίων [34].
Farantos Stavros
2010-09-03
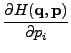
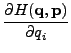
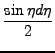
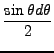
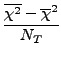 .
.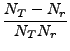
![]() ClO + O2, που υπολογίσθηκε με το δυναμικό της
Παραγράφου 2.3, με τις αντίστοιχες πειραματικές τιμές[25].
ClO + O2, που υπολογίσθηκε με το δυναμικό της
Παραγράφου 2.3, με τις αντίστοιχες πειραματικές τιμές[25].
![$\displaystyle {\frac{{\exp[ij(S_{po}/ \hbar - \alpha_{po} \pi/2)]}}{{[det(M_{po}^j-1)]^{1/2}}}}$](img217.png) .
.