Next: 3. ΗΜΙΚΛΑΣΙΚΗ ΠΡΟΣΕΓΓΙΣΗ ΤΗΣ Up: chemdyn Previous: 1. ΕΙΣΑΓΩΓΗ Contents Index
Η θεωρητική περιγραφή της δυναμικής ενός μορίου ή ενός συστήματος ατόμων και μορίων προϋποθέτει τη λύση της εξίσωσης του Schrödinger για το σύστημα των N πυρήνων και n ηλεκτρονίων. Παρόλη την αισιοδοξία των φυσικών2.1 κατά τα πρώτα χρόνια της εμφάνισης της Κβαντομηχανικής, σήμερα αναγνωρίζεται ότι μια ακριβής λύση της μοριακής εξίσωσης του Schrödinger είναι πρακτικά αδύνατη.
Μια πρώτη προσέγγιση στη λύση αυτού του προβλήματος των πολλών σωμάτων είναι ο διαχωρισμός της ηλεκτρονικής από την πυρηνική κίνηση που υποδεικνύει η μεγάλη διαφορά μάζας μεταξύ πυρήνων και ηλεκτρονίων ( mn/me = 1836). Αυτή είναι η προσέγγιση Born-Oppenheimer[9,10] (Β-Ο), και σημαίνει ότι τα ηλεκτρόνια προσαρμόζουν τις θέσεις τους ακαριαία σε κάθε μετατόπιση των πυρήνων. Με άλλα λόγια, μπορούμε να υποθέσουμε ότι η κίνηση των πυρήνων καθορίζεται από το δυναμικό πεδίο που δημιουργούν τα ηλεκτρόνια. Η κίνηση αυτή καλείται αδιαβατική. Το ηλεκτρονικό πεδίο είναι συνάρτηση των σχετικών αποστάσεων των πυρήνων, και ονομάζεται Αδιαβατική Δυναμική Ενεργειακή Επιφάνεια (ΔΕΕ). Ο Fritz London[11] ήταν ο πρώτος που τόνισε τη σημασία των αδιαβατικών ΔΕΕ στη μελέτη των χημικών αντιδράσεων.
Η έννοια της ΔΕΕ είναι θεμελιώδης για τη Χημεία. Το Σχήμα 2.1 τονίζει τη σημασία της ΔΕΕ και δείχνει τη σύνδεσή της με τη Φασματοσκοπία, τη Χημική Κινητική, καθώς επίσης και άλλους τομείς της Θεωρητικής Χημείας.
Για την καλύτερη κατανόηση της έννοιας της Δυναμικής Ενεργειακής Επιφάνειας, αλλά και των προσεγγίσεων που εισάγονται με τον ορισμό της, είναι απαραίτητο να παρουσιάσουμε τη μαθηματική περιγραφή της προσέγγισης Born-Oppenheimer.
Οι στάσιμες καταστάσεις ενός συστήματος n-ηλεκτρονίων με συντεταγμένες ri, i = 1,..., n, και N-πυρήνων με συντεταγμένες Ra, a = 1,..., N, υπολογίζονται από την χρονοανεξάρτητη εξίσωση του Schrödinger:
![]() είναι ο μη-σχετικιστικός Χαμιλτονιανός τελεστής, και εκφράζεται ως
το άθροισμα της πυρηνικής κινητικής ενέργειας,
(
είναι ο μη-σχετικιστικός Χαμιλτονιανός τελεστής, και εκφράζεται ως
το άθροισμα της πυρηνικής κινητικής ενέργειας,
(![]() nuc),
της ηλεκτρονικής κινητικής ενέργειας,
(
nuc),
της ηλεκτρονικής κινητικής ενέργειας,
(![]() e), και του δυναμικού
Coulomb,
(
e), και του δυναμικού
Coulomb,
(![]() ):
):
| (2.2) |
| [ |
(2.5) |
Από τα παραπάνω γίνεται σαφές ότι στην προσέγγιση Β-Ο οι ηλεκτρονικές
ιδιοενέργειες,
U![]() (
(![]() ), παίζουν τον ρόλο της δυναμικής ενέργειας στην
κίνηση των πυρήνων. Οι U
), παίζουν τον ρόλο της δυναμικής ενέργειας στην
κίνηση των πυρήνων. Οι U![]() είναι συναρτήσεις 3Ν - 6 μεταβλητών (3Ν - 5 για
γραμμικά μόρια), και ορίζουν μία υπερεπιφάνεια σ' ένα 3Ν - 5 (3Ν - 4 για
γραμμικά μόρια) διαστάσεων χώρο. Η U
είναι συναρτήσεις 3Ν - 6 μεταβλητών (3Ν - 5 για
γραμμικά μόρια), και ορίζουν μία υπερεπιφάνεια σ' ένα 3Ν - 5 (3Ν - 4 για
γραμμικά μόρια) διαστάσεων χώρο. Η U![]() είναι η
Αδιαβατική Δυναμική Ενεργειακή Επιφάνεια για την ηλεκτρονική
κατάσταση
είναι η
Αδιαβατική Δυναμική Ενεργειακή Επιφάνεια για την ηλεκτρονική
κατάσταση ![]() .
.
Για διατομικά μόρια το δυναμικό U![]() είναι συνάρτηση μιας μεταβλητής,
της απόστασης μεταξύ των πυρήνων. Στα τριατομικά μόρια η ΔΕΕ είναι συνάρτηση
τριών μεταβλητών, ενώ για τετρατομικά συστήματα ο χώρος των πυρηνικών
θέσεων είναι εξαδιάστατος.
είναι συνάρτηση μιας μεταβλητής,
της απόστασης μεταξύ των πυρήνων. Στα τριατομικά μόρια η ΔΕΕ είναι συνάρτηση
τριών μεταβλητών, ενώ για τετρατομικά συστήματα ο χώρος των πυρηνικών
θέσεων είναι εξαδιάστατος.
Αν και μπορούμε να ισχυρισθούμε ότι το μεγαλύτερο μέρος της Χημείας
μελετάται στα πλαίσια της αδιαβατικής ΔΕΕ, εντούτοις σε ορισμένες
περιπτώσεις τα ολοκληρώματα
< ![]() |
|![]() nuc1/2|
nuc1/2|![]() >
(τα ονομαζόμενα μη-αδιαβατικά ολοκληρώματα), που έχουμε αγνοήσει,
δεν είναι αμελητέα και η προσέγγιση Β-Ο παύει να ισχύει. Αυτό συμβαίνει
όταν δύο δονητικές καταστάσεις βρίσκονται ενεργειακά πλησίον η μία της άλλης
αλλά ανήκουν σε διαφορετικές ηλεκτρονικές καταστάσεις.
Τέτοια είναι τα φαινόμενα
Renner-Teller σε γραμμικά μόρια, και Jahn-Teler σε μη-γραμμικά
μόρια. Τα φαινόμενα αυτά καλούνται μη-αδιαβατικά και έχει βρεθεί
ότι εντοπίζονται σε μια περιορισμένη περιοχή της δυναμικής επιφάνειας.
Τότε, η προσέγγιση Β-Ο παρέχει το πρώτο βήμα στη λύση τέτοιων προβλημάτων.
>
(τα ονομαζόμενα μη-αδιαβατικά ολοκληρώματα), που έχουμε αγνοήσει,
δεν είναι αμελητέα και η προσέγγιση Β-Ο παύει να ισχύει. Αυτό συμβαίνει
όταν δύο δονητικές καταστάσεις βρίσκονται ενεργειακά πλησίον η μία της άλλης
αλλά ανήκουν σε διαφορετικές ηλεκτρονικές καταστάσεις.
Τέτοια είναι τα φαινόμενα
Renner-Teller σε γραμμικά μόρια, και Jahn-Teler σε μη-γραμμικά
μόρια. Τα φαινόμενα αυτά καλούνται μη-αδιαβατικά και έχει βρεθεί
ότι εντοπίζονται σε μια περιορισμένη περιοχή της δυναμικής επιφάνειας.
Τότε, η προσέγγιση Β-Ο παρέχει το πρώτο βήμα στη λύση τέτοιων προβλημάτων.
Ο υπολογισμός μιας ΔΕΕ με μεθόδους ab initio γίνεται με την επίλυση της ηλεκτρονικής εξίσωσης του Schrödinger, Εξίσωση 2.3. Αυτό είναι το έργο της Κβαντικής Χημείας [12,13]. Ο συνήθης τρόπος επιλύσεως της εξίσωσης αυτής είναι με την ανάπτυξη των ιδιοσυναρτήσεων ως ένα άθροισμα γνωστών μαθηματικών συναρτήσεων (συναρτήσεις βάσης) αλλά με άγνωστους τους συντελεστές ανάπτυξης. Εφαρμόζοντας το Θεώρημα των Μεταβολών [12,13] μετατρέπουμε τη διαφορική εξίσωση του Schrödinger σε ένα αλγεβρικό σύστημα γραμμικών εξισώσεων για την εύρεση των συντελεστών. Η μέθοδος περιλαμβάνει:
Ο σπουδαστής που δεν έχει εμπειρία με μοριακούς κβαντοχημικούς υπολογισμούς είναι δύσκολο να συλλάβει την έκταση αυτών των υπολογισμών. Εάν θέλουμε να υπολογίσουμε τις ΔΕΕ επιλύοντας την εξίσωση του Schrödinger ο όγκος των αριθμητικών υπολογισμών αυξάνει εκθετικά με τον αριθμό των ατόμων στο μόριο. Για παράδειγμα σ' ένα τριατομικό σύστημα η ΔΕΕ είναι συνάρτηση τριών μεταβλητών (π.χ. των τριών αποστάσεων μεταξύ των πυρήνων). Εάν η ηλεκτρονική ενέργεια υπολογίζεται για 100 σημεία σε κάθε μεταβλητή, τότε απαιτούνται 106 υπολογισμοί για να έχουμε μια μέτρια αριθμητική περιγραφή της ΔΕΕ. Με την παρούσα τεχνολογία των Η/Υ, υπολογισμοί αυτού του μεγέθους παραμένουν ένα φιλόδοξο πρόγραμμα, τουλάχιστον για τα περισσότερα μόρια με χημικό ενδιαφέρον. Από την άλλη μεριά, η μελέτη της δυναμικής (η μελέτη της κίνησης των πυρήνων) απαιτεί τον υπολογισμό του δυναμικού για ένα μεγάλο αριθμό πυρηνικών θέσεων. Το παρήγορο είναι ότι το λογισμικό για Η/Υ της Κβαντικής Χημείας έχει αναπτυχθεί σε τέτοιο βαθμό που κάνει τους ηλεκτρονικούς υπολογισμούς προσιτούς και από τις πειραματικές ομάδες. Πάντως, χρειάζεται προσοχή όταν ``τρέχουμε'' τέτοια προγράμματα γιατί εύκολα μια κακή βάση συναρτήσεων μπορεί να δώσει λανθασμένα αποτελέσματα.
Τα πακέτα προγραμμάτων GAUSSIAN [14], MOLPRO [15] και TURBOMOL διαθέτουν μια μεγάλη σειρά μεθόδων για τον υπολογισμό των μοριακών τροχιακών με ένα αρκετά μεγάλο φάσμα ακρίβειας, καθώς και προγράμματα για τον υπολογισμό παρατηρήσιμων ποσοτήτων.
Ακριβείς ab initio επιφάνειες έχουν επιτευχθεί μόνο για μερικά απλά μόρια, όπως H3, H2F, και HF2[16]. Στις περισσότερες περιπτώσεις υπολογισμοί ab initio εκτελούνται μόνο για ένα μικρό αριθμό πυρηνικών διατάξεων, ενώ η συνολική μορφολογία της υπερεπιφάνειας συμπεραίνεται από πειραματικά αποτελέσματα.
Όπως αναφέρθηκε στην Παράγραφο 2.2, προϋπόθεση για τη μελέτη της δυναμικής ενός μορίου είναι η γνώση της συνάρτησης του ηλεκτρονικού δυναμικού για μια συγκεκριμένη ηλεκτρονική κατάσταση. Στην πράξη, τα δυναμικά αυτά κατασκευάζονται χρησιμοποιώντας αναλυτικές συναρτήσεις οι οποίες αναπαράγουν τόσο αριθμητικούς υπολογισμούς ab initio όσο και εμπειρικά αποτελέσματα από την Φασματοσκοπία και Χημική Κινητική. Οι φασματοσκοπικές μετρήσεις παρέχουν πληροφορίες για τις σταθερές μορφές των μορίων, οι οποίες αντιστοιχούν στα ελάχιστα της ενεργειακής επιφάνειας. Μετρώντας τις ταχύτητες των αντιδράσεων συμπεραίνουμε την ύπαρξη ή μη ενεργειακών φραγμάτων, που αντιστοιχούν σε σαγματικά σημεία της επιφάνειας.
Είναι πράγματι χρήσιμο μιλώντας για δυναμικές επιφάνειες να έχουμε στο νου τη γεωμετρική εικόνα. Μία επιφάνεια στην οποία εμφανίζονται εξογκώματα, κοιλότητες, πεδιάδες καθώς και άλλα τοπογραφικά χαρακτηριστικά. Γνώση λοιπόν της ΔΕΕ σημαίνει τον εντοπισμό και περιγραφή όλων των ακροτάτων σημείων της συνάρτησης.
Μία αναλυτική συνάρτηση κατάλληλη για την αναπαράσταση μιας ΔΕΕ πρέπει να εκπληρεί τις παρακάτω συνθήκες.
Αναλυτικές συναρτήσεις για τις δυναμικές καμπύλες των διατομικών μορίων είναι γνωστές από πολλά χρόνια. Τέτοιες είναι:
| U(R) = De{exp[- 2 |
(2.7) |
f = 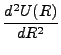 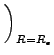 = 2De = 2De |
(2.8) |
| U(R) = 4 |
(2.9) |
Για πολυατομικά μόρια χρησιμοποιούμε διάφορα συστήματα συντεταγμένων για να περιγράψουμε τις ΔΕΕ. Το Σχήμα 2.2 δείχνει τα συνηθέστερα συστήματα για τριατομικά μόρια. Μια τοπική αναλυτική αναπαράσταση της δυναμικής ενέργειας γύρω από τα σημεία ισορροπίας ενός πολυατομικού μορίου μπορεί να γίνει με ανάπτυξη σε σειρά Taylor.
U = 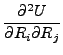 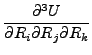 |
(2.10) |
![\includegraphics[scale=0.6]{figures/fig2_2.eps}](img55.png)
|
Η πρώτη συνάρτηση δυναμικού που περιγράφει όλο τον χώρο των πυρηνικών διατάξεων προτάθηκε από τον London[11] για τη θεμελιώδη ηλεκτρονική κατάσταση του συστήματος H3. Οι Eyring και Polanyi[17] χρησιμοποίησαν τον φορμαλισμό του London κατά ένα ημιεμπειρικό τρόπο για τη μελέτη του συστήματος H + H2, και έδειξαν την ύπαρξη ενός σαγματικού σημείου. Πολύ αργότερα ο Sato[18,19] παραμετρικοποίησε τη συνάρτηση LEP (London-Eyring-Polanyi) εισάγοντας μία παράμετρο η οποία αναπαρήγαγε την ενέργεια ενεργοποιήσεως (activation energy) της αντίδρασης. Η μέθοδος έχει τροποποιηθεί περαιτέρω, με την εισαγωγή περισσοτέρων παραμέτρων, και έχει χρησιμοποιηθεί για την κατασκευή δυναμικών επιφανειών που παρουσιάζουν ενεργειακά φράγματα, H2F[20], HCl2[21]. Το κύριο μειονέκτημα των συναρτήσεων LEPS είναι ο μικρός αριθμός των παραμέτρων που εισαγάγει, πράγμα που κάνει τη συνάρτηση μη ικανή να αναπαράγει την πολύπλοκη μορφολογία της ΔΕΕ όπως αυτή εμφανίζεται στις χημικά ενδιαφέρουσες περιπτώσεις.
Η δυνατότητα επέκτασης της συνάρτησης Morse, που κατά κόρον έχει χρησιμοποιηθεί στα διατομικά μόρια, σε τριατομικά συστήματα, έχει κατά πρώτον διερευνηθεί από τους Wall και Porter[22]. Η προτεινόμενη συνάρτηση έχει χρησιμοποιηθεί επίσης σε συνδυασμό με τη μέθοδο spline για την προσαρμογή υπολογισμών ab initio. Η τεχνική αυτή παρουσιάζει αρκετά μειονεκτήματα, όπως η δυσκολία να επεκταθεί σε πολλές διαστάσεις, καθώς και σε πολυατομικά μόρια: τα παραγόμενα δυναμικά έχουν ασυνέχειες.
Πάμπολλες συναρτήσεις έχουν προταθεί οι οποίες όμως δεν ικανοποιούν μία ή περισσότερες από τις συνθήκες 1-4.
Μία συστηματική μέθοδος για την κατασκευή πολυατομικών δυναμικών επιφανειών
που πληρούν τις συνθήκες 1-4, είναι η μέθοδος της ανάπτυξης της ΔΕΕ σε μία
σειρά των πολλών σωμάτων (many-body expansion)[23].
Η Εξίσωση 2.11 αποκαλύπτει αμέσως ένα σημαντικό πλεονέκτημα της μεθόδου. Άπαξ και έχουμε βρει τα διατομικά δυναμικά, αυτά μπορούν να χρησιμοποιηθούν στην κατασκευή τριατομικών δυναμικών. Το ίδιο ισχύει για τα δυναμικά των τριών σωμάτων που χρησιμοποιούνται στην κατασκευή των τετρατομικών δυναμικών.
Η συναρτησιακή μορφή που επιλέχθηκε για την περιγραφή των όρων της Εξίσωσης 2.11 είναι η εξής:
| U(k) = P( |
(2.12) |
| P(s1, s2, s3) = c0 + |
(2.13) |
T είναι μία συνάρτηση που δίνει στο δυναμικό τη σωστή ασυμπτωτική
συμπεριφορά, δηλ.
T ![]() 0, εάν μία από τις μεταβλητές τείνει στο
άπειρο.
0, εάν μία από τις μεταβλητές τείνει στο
άπειρο.
Οι όροι των 2-σωμάτων έχουν τη μορφή:
| UAB(R1) = - De(1 + c1r + c2r2 + c3r3)exp(- c1r) | (2.14) |
Για τους όρους U(3), καθώς και ανώτερους όρους, έχει βρεθεί ότι η ασυμπτωτική συνάρτηση T εκφραζόμενη ως,
| T = |
(2.15) |
Ας εξετάσουμε τώρα μερικά παραδείγματα μορίων στα οποία έχει εφαρμοσθεί η μέθοδος των πολλών σωμάτων.
| S1(A1) | R1 - R10 | ||||
| S2(E) | = | 0 | - | R2 - R20 | |
| S3(E) | - | - | R3 - R30 |
| U = | |
| U(2)(ri) = | -5, 213[1 + 3, 7537ri]exp(- 3, 7537ri), ri = Ri - 1, 2074 |
| U(3) = | [P(Si) + G(Si)][1 - tanh(4, 6S1/2)] |
| P(Si) = | 8, 7066 + 6, 5822S1 +13, 9106S12 -17, 1931(S22 + S32) - |
| 3, 1421S1(S22 + S32) + 2, 6323S3(S32 -3S22) + 13, 9659(S22 + S32)2 | |
| G(Si) = | -3, 0 exp[- 7, 5(S22 + S32)], Ri0 = 1, 5698 |
Το Σχήμα 2.3 δείχνει τις ισοδυναμικές καμπύλες της υπερεπιφάνειας
οι οποίες κατασκευάζονται από την κίνηση ενός ατόμου οξυγόνου γύρω από
το μοριακό οξυγόνο. Λόγω της συμμετρίας του δυναμικού ως προς τον άξονα Υ,
η συνάρτηση υπολογίζεται μόνο στο ένα τεταρτημόριο του επιπέδου. Διακρίνουμε
το απόλυτο ελάχιστο (συμμετρίας C2v), και ένα δεύτερο ελάχιστο πάνω
στον άξονα των Υ που αντιστοιχεί στο μετασταθές όζον με συμμετρία D3h.
Παρατηρούμε ότι το παρόν δυναμικό δεν έχει ενεργειακό φράγμα καθώς
απομακρύνουμε ένα άτομο οξυγόνου στο άπειρο και για συμμετρίες Cs.
Αντιθέτως, υπάρχει ενεργειακό φράγμα όταν το άτομο απομακρύνεται κατά
μήκος του άξονα C2v.
Η θεμελιώδης ηλεκτρονική κατάσταση του τριοξειδίου του χλωρίου
σχετίζεται αδιαβατικά με τα παρακάτω προϊόντα διάσπασης:
| ClO3 | Cl (2P) + O3(1A') | ||
| O(3P) + ClO2(2A') | |||
| ClO(2 |
(2.16) |
Επομένως το δυναμικό γράφεται ως εξής:
| UClO3 | = | 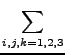 UClO2(3)(Ri, Rj, Rk) + UClO2(3)(Ri, Rj, Rk) + |
|
| UO3(3)(R4, R5, R6) + UClO3(4)(Ri, i = 1,..., 6). | (2.17) |
Τα δυναμικά των O2, ClO, ClO2, O3, και ClO3 έχουν χρησιμοποιηθεί για τη μελέτη της παγίδευσης του όζοντος από το ατομικό χλώριο (Εξισώσεις 1.3) [25].
Οι χημικές αντιδράσεις που συμβαίνουν στην άνω ατμόσφαιρα είναι συνήθως αντιδράσεις ελευθέρων ριζών και επομένως αρκετά γρήγορες. Η πειραματική μέτρηση των ταχυτήτων τέτοιων αντιδράσεων είναι δύσκολη. Μία θεωρητική πρόβλεψη είναι λοιπόν αναγκαία και αυτό προϋποθέτει τη λύση της πυρηνικής εξίσωσης του Schrödinger (Εξίσωση 2.6). Αν και έχει γίνει τεράστια πρόοδος στην κβαντική μελέτη των χημικών αντιδράσεων [26], εν τούτοις μια ρεαλιστική μελέτη των χημικών αντιδράσεων γίνεται στα πλαίσια της κλασικής μηχανικής με τη μέθοδο των κλασικών τροχιών. Στο επόμενο κεφάλαιο περιγράφουμε την κλασική και ημικλασική προσέγγιση για τη μελέτη της Μοριακής Δυναμικής.