QR Factorization

The traditional algorithm for QR factorization is based on the use of elementary Householder matrices of the general form

$$H = I - \tau v v^T$$

where v is a column vector and 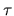$\tau$ is a scalar. This leads to an algorithm with very good vector performance, especially if coded to use Level 2 BLAS.

The key to developing a block form of this algorithm is to represent a product of b elementary Householder matrices of order n as a block form of a Householder matrix. This can be done in various ways. LAPACK uses the following form [90]:

$$H_1 H_2 \ldots H_b = I - V T V^T$$

where V is an n-by-b matrix whose columns are the individual vectors 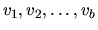$v_1, v_2, \ldots , v_b$ associated with the Householder matrices 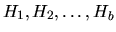$H_1, H_2, \ldots , H_b$, and T is an upper triangular matrix of order b. Extra work is required to compute the elements of T, but once again this is compensated for by the greater speed of applying the block form. Table 3.10 summarizes results obtained with the LAPACK routine DGEQRF.

Table 3.10: Speed in megaflops of DGEQRF for square matrices of order n

	No. of	Block	Values of n
	processors	size	100	1000
Dec Alpha Miata	1	28	141	363
Compaq AlphaServer DS-20	1	28	326	444
IBM Power 3	1	32	244	559
IBM PowerPC	1	52	45	127
Intel Pentium II	1	40	113	250
Intel Pentium III	1	40	135	297
SGI Origin 2000	1	64	173	451
SGI Origin 2000	4	64	55	766
Sun Ultra 2	1	64	20	230
Sun Enterprise 450	1	64	48	329