Eigenvalues, Eigenvectors and Generalized Schur Decomposition

Let A and B be n-by-n matrices. A scalar $\lambda$ is called a generalized eigenvalue and a non-zero column vector x the corresponding right generalized eigenvector of the pair (A,B), if $Ax = \lambda Bx$. A non-zero column vector y satisfying $y^H A = \lambda y^H B$ is called the left generalized eigenvector corresponding to $\lambda$. (For simplicity, we will usually omit the word ``generalized'' when no confusion is likely to arise.) If B is singular, we can have the infinite eigenvalue $\lambda = \infty$, by which we mean Bx = 0. Note that if A is non-singular, then the equivalent problem $\mu Ax = Bx$ is perfectly well-defined, and the infinite eigenvalue corresponds to $\mu = 0$. The generalized symmetric definite eigenproblem in section 2.3.7 has only finite real eigenvalues. The generalized nonsymmetric eigenvalue problem can have real, complex or infinite eigenvalues. To deal with both finite (including zero) and infinite eigenvalues, the LAPACK routines return two values, $\alpha$ and $\beta$. If $\beta$ is non-zero then $\lambda = \alpha/\beta$ is an eigenvalue. If $\beta$ is zero then $\lambda = \infty$ is an eigenvalue of (A, B). (Round off may change an exactly zero $\beta$ to a small nonzero value, changing the eigenvalue $\lambda = \infty$ to some very large value; see section 4.11 for details.) A basic task of these routines is to compute all n pairs $(\alpha,\beta)$ and x and/or y for a given pair of matrices (A,B).

If the determinant of $A - \lambda B$ is identically zero for all values of $\lambda$, the eigenvalue problem is called singular; otherwise it is regular. Singularity of (A,B) is signaled by some $\alpha = \beta = 0$ (in the presence of roundoff, $\alpha$ and $\beta$ may be very small). In this case, the eigenvalue problem is very ill-conditioned, and in fact some of the other nonzero values of $\alpha$ and $\beta$ may be indeterminate (see section 4.11.1.4 for further discussion) [93,105,29,53].

Another basic task is to compute the generalized Schur decomposition of the pair (A,B). If A and B are complex, then their generalized Schur decomposition is A = QSZ^H and B = QTZ^H, where Q and Z are unitary and S and T are upper triangular. The LAPACK routines normalize T to have real non-negative diagonal entries. Note that in this form, the eigenvalues can be easily computed from the diagonals: $\lambda_i = s_{ii}/t_{ii}$ (if $t_{ii} \neq 0$) and $\lambda_i = \infty$ (if t_ii = 0), and so the LAPACK routines return $\alpha_i = s_{ii}$ and $\beta_i = t_{ii}$.

The generalized Schur form depends on the order of the eigenvalues on the diagonal of (S,T). This order may optionally be chosen by the user.

If A and B are real, then their generalized Schur decomposition is A = QSZ^T and B = QTZ^T, where Q and Z are orthogonal, S is quasi-upper triangular with 1-by-1 and 2-by-2 blocks on the diagonal, and T is upper triangular with non-negative diagonal entries. The structure of a typical pair of (S,T) is illustrated below for n=6:

$$S = \left( \begin{array}{cccccc} \times & \times & \times &... ...\times & 0 \\ 0 & 0 & 0 & 0 & 0 & \times \end{array} \right)$$

The 1 x 1 diagonal blocks of (S,T) (those in the (1,1) and (4,4) positions) contain the real eigenvalues of (A,B) and the 2 x 2 diagonal blocks of (S,T) (those in the (2:3,2:3) and (5:6,5:6) positions) contain conjugate pairs of complex eigenvalues of (A,B). The 2 x 2 diagonal blocks of T corresponding to 2-by-2 blocks of S are made diagonal. This arrangement enables us to work entirely with real numbers, even when some of the eigenvalues of (A,B) are complex. Note that for real eigenvalues, as for all eigenvalues in the complex case, the $\alpha_i$ and $\beta_i$ values corresponding to real eigenvalues may be easily computed from the diagonals of S and T. The $\alpha_i$ and $\beta_i$ values corresponding to complex eigenvalues of a 2-by-2 diagonal block of (S,T) are computed by first computing the complex conjugate eigenvalues $\lambda$ and $\bar{\lambda}$ of the block, then computing the values of $\beta_i$ and $\beta_{i+1}$ that would result if the block were put into complex generalized Schur form, and finally multiplying to get $\alpha_i = \lambda \beta_i$ and $\alpha_{i+1}=\bar{\lambda}\beta_{i+1}$.

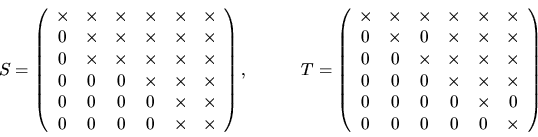
The columns of Q and Z are called generalized Schur vectors and span pairs of deflating subspaces of A and B [94]. Deflating subspaces are a generalization of invariant subspaces: the first k columns of Z span a right deflating subspace mapped by both A and B into a left deflating subspace spanned by the first k columns of Q. This pair of deflating subspaces corresponds to the first k eigenvalues appearing at the top left corner of S and T as explained in section 2.3.5.2.

The computations proceed in the following stages:

1.

The pair (A,B) is reduced to generalized upper Hessenberg form. If A and B are real, this decomposition is A = UHV^T and B = U R V^T where H is upper Hessenberg (zero below the first subdiagonal), R is upper triangular, and U and V are orthogonal. If A and B are complex, the decomposition is A = UHV^H and B = URV^H with U and V unitary, and H and R as before. This decomposition is performed by the subroutine xGGHRD, which computes H and R, and optionally U and/or V. Note that in contrast to xGEHRD (for the standard nonsymmetric eigenvalue problem), xGGHRD does not compute U and V in a factored form.

2.

The pair (H,R) is reduced to generalized Schur form H = QSZ^T and R = QTZ^T (for H and R real) or H = QSZ^H and R = QTZ^H (for H and R complex) by subroutine xHGEQZ. The values $\alpha_i$ and $\beta_i$ are also computed, where $\lambda_i = \alpha_i / \beta_i$ are the eigenvalues. The matrices Z and Q are optionally computed.

3.

The left and/or right eigenvectors of the pair (S,T) are computed by xTGEVC. One may optionally transform the right eigenvectors of (S,T) to the right eigenvectors of (A,B) (or of (H,R)) by passing (UQ,VZ) (or (Q,Z)) to xTGEVC.

Other subsidiary tasks may be performed before or after those described.