




Next: Troubleshooting
Up: Installing LAPACK Routines
Previous: Points to Note
Contents
Index
Installing ILAENV
Machine-dependent
parameters such as the block size are set
by calls to an inquiry function which may be set with different
values on each machine.
The declaration of the environment inquiry function is
INTEGER FUNCTION ILAENV( ISPEC, NAME, OPTS, N1, N2, N3, N4 )
where ISPEC, N1, N2, N3, and N4 are integer variables and
NAME and OPTS are CHARACTER*(*). NAME specifies the subroutine name:
OPTS is a character string of options to the subroutine; and N1-N4 are
the problem dimensions.
ISPEC specifies the parameter to be returned; the following values are
currently used in LAPACK:
ISPEC = 1: NB, optimal block size
= 2: NBMIN, minimum block size for the block routine to be used
= 3: NX, crossover point (in a block routine, for N < NX, an unblocked
routine should be used)
= 4: NS, number of shifts
= 6: NXSVD is the threshold point for which the QR
factorization is performed prior to reduction to
bidiagonal form. If M > NXSVD 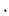 N, then a
N, then a
QR factorization is performed.
= 8: MAXB, crossover point for block multishift QR
= 9: SMLSIZ, maximum size of the subproblems at the
bottom of the computation tree in the divide-and-conquer
algorithm
= 10: NAN, IEEE NaN arithmetic can be trusted not to trap
= 11: INFINITY, infinity arithmetic can be trusted not to trap
The three block size parameters, NB, NBMIN, and NX, are used in many
different
subroutines (see Table 6.1).
NS and MAXB are used in the
block multishift QR algorithm, xHSEQR.
NXSVD is used in the driver
routines xGELSS and xGESVD.
SMLSIZ is used in the
divide and conquer routines xBDSDC, xGELSD, xGESDD, and xSTEDC.
The parameters NAN and INFINITY are used in the driver routines
xSTEVR and xSYEVR/xCHEEVR to check for IEEE-754 compliance. If
compliance is detected, then these driver routines call xSTEGR.
Otherwise, a slower algorithm is selected.
Table 6.1:
Use of the block parameters NB, NBMIN, and NX in LAPACK
| real |
complex |
NB |
NBMIN |
NX |
| SGBTRF |
CGBTRF |
 |
|
|
| SGEBRD |
CGEBRD |
 |
 |
 |
| SGEHRD |
CGEHRD |
 |
 |
 |
| SGELQF |
CGELQF |
 |
 |
 |
| SGEQLF |
CGEQLF |
 |
 |
 |
| SGEQRF |
CGEQRF |
 |
 |
 |
| SGERQF |
CGERQF |
 |
 |
 |
| SGETRF |
CGETRF |
 |
|
|
| SGETRI |
CGETRI |
 |
 |
|
| SORGLQ |
CUNGLQ |
 |
 |
 |
| SORGQL |
CUNGQL |
 |
 |
 |
| SORGQR |
CUNGQR |
 |
 |
 |
| SORGRQ |
CUNGRQ |
 |
 |
 |
| SORMLQ |
CUNMLQ |
 |
 |
|
| SORMQL |
CUNMQL |
 |
 |
|
| SORMQR |
CUNMQR |
 |
 |
|
| SORMRQ |
CUNMRQ |
 |
 |
|
| SPBTRF |
CPBTRF |
 |
|
|
| SPOTRF |
CPOTRF |
 |
|
|
| SPOTRI |
CPOTRI |
 |
|
|
| SSTEBZ |
|
 |
|
|
| SSYGST |
CHEGST |
 |
|
|
| SSYTRD |
CHETRD |
 |
 |
 |
| SSYTRF |
CHETRF |
 |
 |
|
| |
CSYTRF |
 |
 |
|
| STRTRI |
CTRTRI |
 |
|
|
|
The LAPACK testing and timing programs use a special version of ILAENV
where the parameters are set via a COMMON block interface.
This is convenient for experimenting with different values of, say,
the block size in order to exercise different parts of the code
and to compare the relative performance of different parameter values.
The LAPACK timing programs were designed to collect data for all of the
routines in Table 6.1.
The range of problem sizes needed to determine the optimal block size
or crossover point is machine-dependent, but the
input files
provided with the LAPACK test and timing package can be used as a
starting point.
For subroutines that require a crossover point, it is best to start by
finding the best block size with the crossover
point set to 0, and then
to locate the point at which the performance of the unblocked algorithm
is beaten by the block algorithm.
The best crossover point
will be somewhat smaller than the point
where the curves for the unblocked and blocked methods cross.
For example, for SGEQRF on a single processor of a CRAY-2,
NB = 32 was observed to be a good block size,
and the performance of the block algorithm with this block size
surpasses the unblocked algorithm for square matrices
between N = 176 and N = 192.
Experiments with crossover points from 64 to 192 found that NX = 128
was a good choice, although the results for NX from 3*NB to 5*NB
are broadly similar.
This means that matrices with 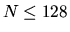 should use the unblocked
algorithm, and for N > 128 block updates should be used until the
remaining submatrix has order less than 128.
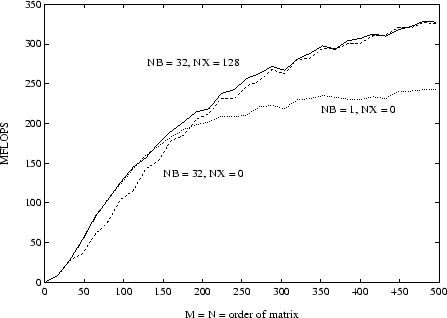
The performance of the unblocked (NB = 1) and blocked (NB = 32)
algorithms for SGEQRF and for the blocked algorithm with a crossover
point of 128 are compared in Figure 6.1.
should use the unblocked
algorithm, and for N > 128 block updates should be used until the
remaining submatrix has order less than 128.
The performance of the unblocked (NB = 1) and blocked (NB = 32)
algorithms for SGEQRF and for the blocked algorithm with a crossover
point of 128 are compared in Figure 6.1.
Figure 6.1:
QR factorization on CRAY-2 (1 processor)
 |
By experimenting with small values of the block size,
it should be straightforward to choose NBMIN,
the smallest block size that gives a performance improvement
over the unblocked algorithm.
Note that on some machines, the optimal block size may be 1
(the unblocked algorithm gives the best performance);
in this case, the choice of NBMIN is arbitrary.
The prototype version of ILAENV sets NBMIN to 2, so that blocking
is always done, even though this could lead to poor performance
from a block routine if insufficient workspace is supplied
(see chapter 7).
Complicating the determination of optimal parameters is the fact that
the orthogonal factorization routines and SGEBRD accept non-square
matrices as input.
The LAPACK timing program allows M and N to be varied independently.
We have found the optimal block size to be
generally insensitive to the shape of the matrix,
but the crossover point is more dependent on the matrix shape.
For example, if M >> N in the QR factorization, block updates
may always be faster than unblocked updates on the remaining submatrix,
so one might set NX = NB if 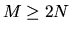 .
.
Parameter values for the number of shifts, etc.
used to tune the block multishift QR
algorithm
can be varied from the input files to the eigenvalue timing program.
In particular, the performance of xHSEQR is particularly sensitive to
the correct choice of block parameters. Setting NS = 2 will give
essentially the same performance as EISPACK.
Interested users should consult [3] for a description of
the timing program input files.





Next: Troubleshooting
Up: Installing LAPACK Routines
Previous: Points to Note
Contents
Index
Susan Blackford
1999-10-01
