


Next: Discussion
Up: Long Write-Up
Previous: Limitations
We conducted certain tests to measure the efficiency of AUTO_DERIV.
We have calculated
the elapsed time during the computation of the value and
the derivatives of functions for which the corresponding analytic
expressions were known. In each test, we use a version of the FORTRAN 90
code with the derivatives
computed analytically, ``by hand'', and another incorporating AUTO_DERIV.
The first mathematical function we used is the Potential Energy Surface
for the HCP molecule, described in [12].
It is a realistic example of a function depending on three variables
and it is sufficiently complex for the purpose of exhibiting the
capabilities of AUTO_DERIV.
Another test was made with the potential for the HF-dimer [13],
a function of six variables. For this we where able to
calculate analytically the first derivatives only.
In Table 1 we present
the elapsed time, averaged over 1000 evaluations, during the computation
of each potential and for the two versions (analytic derivatives and using
AUTO_DERIV). The results are tabulated for the compilers we had available.
The standard DATE_AND_TIME subroutine was employed.
Table 1:
Elapsed times during the calculations of the derivatives of Potential Energy Surfaces for the molecular systems HCP and HF-dimer. Time quoted in ms.
| Potential |
Compiler |
Order of derivatives |
| |
|
0 |
1 |
2 |
| HCP (analytic) |
NAG |
0.626 |
1.155 |
2.612 |
| HCP (AUTO_DERIV) |
NAG |
8.465 |
38.147 |
83.975 |
| HCP (analytic) |
PGI |
0.712 |
1.217 |
2.451 |
| HCP (AUTO_DERIV) |
PGI |
9.105 |
355.795 |
807.796 |
| HCP (analytic) |
Fujitsu |
0.690 |
1.270 |
2.703 |
| HCP (AUTO_DERIV) |
Fujitsu |
10.279 |
66.731 |
142.812 |
| HCP (analytic) |
Absoft |
0.667 |
1.288 |
2.973 |
| HCP (AUTO_DERIV) |
Absoft |
16.075 |
68.494 |
156.458 |
| HF dimer (analytic) |
NAG |
0.071 |
0.752 |
- |
| HF dimer (AUTO_DERIV) |
NAG |
1.807 |
5.302 |
14.250 |
| HF dimer (analytic) |
PGI |
0.152 |
0.518 |
- |
| HF dimer (AUTO_DERIV) |
PGI |
1.142 |
39.513 |
103.397 |
| HF dimer (analytic) |
Fujitsu |
0.075 |
0.596 |
- |
| HF dimer (AUTO_DERIV) |
Fujitsu |
1.903 |
9.335 |
23.231 |
| HF dimer (analytic) |
Absoft |
0.086 |
1.315 |
- |
| HF dimer (AUTO_DERIV) |
Absoft |
3.174 |
10.434 |
22.812 |
|
The tests were performed on an Intel Pentium II processor at 450 MHz, running
the GNU/Linux operating system. We have also compiled and run the programs
on IBM RS/6000 and on HP-PA 2.0 processors with the system's compilers;
these results are not presented here. In the test we used the F90/95
compilers shown in Table 2; the options chosen should
be the optimal ones.
Table:
FORTRAN 90/95 compilers used for the test runs.
| COMPILER |
OPTIONS |
 |
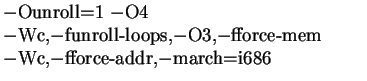 |
| Portland Group, Inc. pgf90 v3.0 |
-fast -tp p6 |
| Fujitsu F90 |
-O3 -Kfast,eval,PENTIUM_PRO -AR |
| Absoft Pro Fortran 6.0 f90 v2.1 |
-B100 -O |
|
The required memory during the tests, naturally, depends directly on the
specific function differentiated. As we use a TYPE (func) variable holding
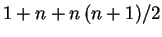 REAL(dpk) numbers
for each REAL(dpk) mathematical variable in the original code
we expect a roughly proportional increase in memory taken by the program.
REAL(dpk) numbers
for each REAL(dpk) mathematical variable in the original code
we expect a roughly proportional increase in memory taken by the program.



Next: Discussion
Up: Long Write-Up
Previous: Limitations
Stavros Farantos
1999-12-11