Example

An example of how to use AUTO_DERIV is the following:

Let us assume that we want to evaluate the first and (possibly) the second derivatives of the mathematical function f with respect to three variables x, y, and z encoded in the subroutine in Fig. 1. Note that it is not necessary to use a function or, even, only one procedure, as we will see.

Figure 1: Routine implementing a test function to be differentiated.

The modifications which are needed in this subroutine in order to evaluate the derivatives are the following:

We should augment the argument list with additional variables to hold the first and (if required) the second derivatives and, also, we should specify, either in the procedure or through an argument, the order of the derivatives we want. In order to use the same subroutine for both first and second order differentiation let us pass an integer (deriv); different values of it will choose different order. Another way to do this is to use the facilities of the optional and keyword arguments of F90: over-simplifying, we can pass only those variables we need to be filled. The former approach enables us to call the subroutine from a F77 code or other programming languages lacking the concept of optional arguments; in the example we will follow this method.

There is no requirement imposed by AUTO_DERIV for the type, the number or, even, the existence of these additional variables. For simplicity we will pass a rank-1 array (Df) with n real elements to hold the first derivatives, and another rank-1 array (DDf) with 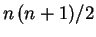$n\,(n + 1) / 2$ elements which will hold the upper triangle of the Hessian matrix (H), where n is the number of independent variables. In our example n = 3 so, in F90 notation the array DDf is:

DDf = (/ H₁₁, H₁₂, H₁₃, H₂₂, H₂₃, H₃₃ /).

Additionally, we will indicate with deriv = 1 that we need only the first derivatives and with deriv = 2 that we require both first and second derivatives.

The definition of the subroutine incorporating these changes and the necessary calls from deriv_class are presented in Fig. 2.

Figure 2: Modification of the routine presented in Fig. 1 for computing the first and second derivatives of function f by incorporating deriv_class.

In order to preserve the same form of the statements in the main part of the subroutine, we reserve the names x,y,z,f for the new variables of TYPE (func), and we use other names, ( 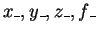$x\_, y\_, z\_, f\_$) for their values.

The programmer should make the following modifications before applying AUTO_DERIV:

In module deriv_class:

.

Assign the number of independent variables to the variable n.

.

Change, if necessary, the kind variable dpk to the appropriate value for the input variables. The default is to have double precision. If required, the other kind variables spk and ik, provided to cope with mixed mode arithmetic, can be changed. Currently AUTO_DERIV supports all expressions among variables of the types REAL (dpk), REAL (spk), and INTEGER (ik).

In the user's subroutine or function:

.

Change the names of the input and output variables in the argument list and declare them as REAL having the same kind as in deriv_class. Their previous names should be used for the variables declared as TYPE (func).

.

Make deriv_class accessible through USE. If necessary, rename the few public variables provided by deriv_class to avoid name clashes with local entities. For example, USE mod, newname => oldname imports the variable oldname from module mod, but with the name newname. The public entities of deriv_class are: the subroutines derivative, independent, extract, the type (func), and, of course, all operators and many intrinsic F90 functions.

.

Declare as TYPE (func) all variables corresponding to mathematical functions; that is, both dependent and independent, and also, all intermediate (dependent) variables. Note, that the use of IMPLICIT typing is permissible; this practice, however, has the side-effect of declaring constants and other variables not related to the differentiation as variables in the mathematical sense. This is not wrong as their derivatives are zeroed, it is only a waste of memory and triggers unnecessary computations. It is regarded as ``good programming style'' to avoid implicit declarations.

.

Define the order of derivatives by calling the subroutine derivative. The integer argument passed (deriv) should have the value of 0, 1, or 2 indicating that we require the computation of the value of the function (included for symmetry and testing), the value and the first derivatives or the value, the first and the second derivatives respectively.

.

Declare the independent variables, their order and value, by calling the subroutine independent separately for each variable.

.

After the final assignment to the dependent variable, extract the derivatives and the value of the function. The subroutine extract, will return the derivatives in rank-1 arrays holding the gradient and the upper triangle of the Hessian.

Note, that the statements in the main body of the subroutine need not be altered. In fact, AUTO_DERIV was designed in such a way that almost no modification of the existing code is required.