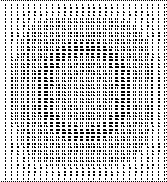
Μεταβλητές Προγράμματος

    Οι μεταβλητές που χρησιμοποιεί το πρόγραμμα είναι οι εξής :

IOP (ακέραιος)                         :   Παίρνει τις τιμές 1 - για μία κυματοσυνάρτηση - , 2 - για δύο κυματοσυναρτήσεις - και ορίζει τις Ψ₁ και Ψ₂ αντίστοιχα
Χ,Υ (πραγματικοί)                    :   Διαστάσεις κουτιού (σταθερές από το πρόγραμμα σε Χ=50, Υ=28)
Ν1Χ, Ν1Υ (ακέραιοι)               :   Κβαντικοί αριθμοί για την Ψ₁.
N2X, N2Y (ακέραιοι)               :   Κβαντικοί αριθμοί για την Ψ₂.
PS1(51,30) (πίνακας 51x30)     :   Κυματοσυνάρτηση Ψ₁(n_1x,n_1y)
PS2(51,30) (πίνακας 51x30)     :   Κυματοσυνάρτηση Ψ₂(n_2x,n_2y)
PS12(51,30) (πίνακας 51x30)   :   Κυματοσυνάρτηση Ψ₁.Ψ₂.
XX (πραγματικός)                     :  Ολοκλήρωμα της PS12 στο  x,y-χώρο
 
Δεδομένα από το Χρήστη

    Από το χρήστη μπορούν να εισαχθούν τα εξής δεδομένα :

IOP (ακέραιος)              : 1 ή 2
Ν1Χ, Ν1Υ (ακέραιοι)    :  Κβαντικοί αριθμοί για την Ψ₁.
N2X, N2Y (ακέραιοι)    :  Κβαντικοί αριθμοί για την Ψ₂ (εάν IOP=2) .

Εκτέλεση προγράμματος
 
    Για να μπορέσουμε να εκτελέσουμε το πρόγραμμα πρέπει να το μετατρέψουμε σε κώδικα μηχανής (executable) . Αυτό θα γίνει με τη χρήση ενός compiler π.χ. το  xlf (σε Unix σύστημα).
Η εντολή είναι     xlf -o twobox twobox.f.     Το αρχείο twobox που δημιουργείται αποτελεί το εκτελέσιμο
αρχείο.
    Οταν τρέξουμε το twobox και δώσουμε τις τιμές που μας ζητούνται βλέπουμε έναν πίνακα με αριθμούς. Η αριθμοί αυτοί αντιστοιχούν στις τιμές της κυματοσυνάρτησης στον άξονα των z, δηλαδή στό ύψος. Αν ενώσουμε με μία γραμμή όλους τους ίδιους αριθμούς έχουμε τις ισοϋψείς καμπύλες.
    Το αρχείο twobox.out που δημιουργείται κάθε φορά που τρέχουμε το πρόγραμμα περιέχει τις συντεταγμένες για τρισδίαστατη αναπαράσταση των αποτελεσμάτων. Αυτή μπορεί να γίνει με ένα μαθηματικό πακέτο όπως το gnuplot για Unix και PC ή το Origin για PC.

Αποτελέσματα

    Μερικά παραδείγματα....
 
Οι εικόνες που φαίνονται παρακάτω αποτελούν τη σμίκρυνση των αρχείων κειμένου που δημιουργεί το πρόγραμμα. Είναι πίνακες με αριθμούς και όταν ενώσουμε όλους τους ίδιους αριθμούς με γραμμές έχουμε τις ισοϋψείς γραμμές . Με τι σμίκρυνση εδώ είναι δυνατό να διακρίνουμε τις περιοχές που έχουν τους ίδιους αριθμούς.
Ετσι για τις παρακάτω τιμές έχουμε

α)    ΙΟΡ = 1 , Ν1Χ = 1,  Ν1Υ= 1
      (1,1,1)
 

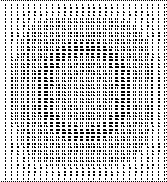
β) ΙΟP=1, Ν1Χ=1,Ν1Y=2        γ) ΙΟΡ=1,Ν1Χ=2,Ν1Υ=1         δ)ΙΟΡ=1,Ν1Χ=2,Ν1Υ=2
(1,1,2)                                          (1,2,1)                                        (1,2,2)
  

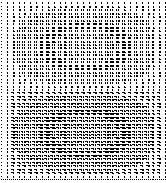
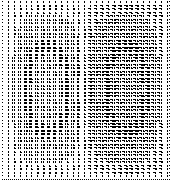
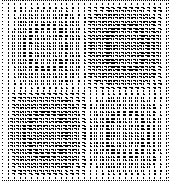
ε) ΙΟΡ=1,Ν1Χ=1, Ν1Υ=3        στ) ΙΟΡ=1,Ν1Χ=3,Ν1Υ=1         ζ) ΙΟΡ=1,Ν1Χ=3,Ν1Υ=3
    (1,1,3)                                        (1,3,1)                                        (1,3,3)
  
 
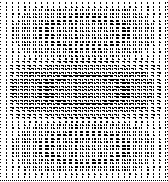
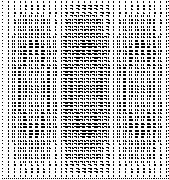
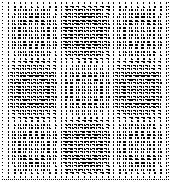
Επίσεις παρόμοια αποτελέσματα μπορείτε να έχεται από αυτό το αρχείο Excel που δημιούργησε ο Κώστας Τσιγαρίδης
 
 

Η σελίδα αυτή δημιουργήθηκε από τον  Ματζαπετάκη Μανόλη