Γενικά Περί μοριακών
Ιδιοσυναρτήσεων
Η μαθηματική περιγραφή ενός χημικού συστήματος γίνεται
με τη βοήθεια της εξίσωσης του Schrodinger.
ΗΨi = ΕiΨi
(1)
όπου Η είναι ο Χαμιλτονιανός τελεστής, Ψi η ιδιοσυνάρτηση
και Εi η ιδιοενέργεια του συστήματος. Η εύρεση των λύσεων της
εκίσωσης αυτής συνήθως επιτυγχάνεται με την ανάπτυξη των λύσεων της Ψi
σε μια βάση γνωστών συναρτήσεων. Χμ, μ=1,2,3,...,n.:
 (2)
Αν αντικαταστήσουμε την εξίσωση (2) στην (1),
πολλαπλασιάσουμε και τα δύο μέρη της προκύπτουσας εξίσωσης με Χν
από αριστερά και τέλος ολοκληρώσουμε και τα δύο μέλη της νέας εξίσωσης
σε όλο το χώρο ορισμού της Χμ οδηγούμαστε στο αλγεβρικό σύστημα
εξισώσεων :
(2)
Αν αντικαταστήσουμε την εξίσωση (2) στην (1),
πολλαπλασιάσουμε και τα δύο μέρη της προκύπτουσας εξίσωσης με Χν
από αριστερά και τέλος ολοκληρώσουμε και τα δύο μέλη της νέας εξίσωσης
σε όλο το χώρο ορισμού της Χμ οδηγούμαστε στο αλγεβρικό σύστημα
εξισώσεων :
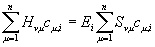 (3)
όπου
(3)
όπου
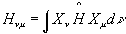 (4)
(4)
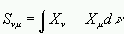 (5)
(5)
Αυτά ονομάζονται Χαμιλτονιανό ολοκλήρωμα και ολοκλήρωμα
επικάλυψης αντίστοιχα
Οι εξισώσεις (3) μπορούν μα γραφούν σε μια πιο συμπαγή
μορφή χρησιμοποιώντας τους πίνακες των αριθμών Ηνμ και Sνμ
:
Η c = S c E (6)
όπου c είναι ένας πίνακας οι στήλες του οποίου περιέχουν
τους συντελεστές της ανάπτυξης στην εξίσωση (2), cμ,i.
Ε είναι ένας διαγώνιος πίνακας n x n, τα διαγώνια στοιχεία του οποίου
είναι οι ιδιοενέργειες. Μια συνηθισμένη προσέγγιση είναι να θεωρήσουμε
τον πίνακα με το ολοκλήρωμα επικάλυψης ως μοναδιαίο:
S = I (7)
οπότε η εξίσωση (6) παίρνει τη μορφή μιας εξίσωσης ιδιοτιμών
και ιδιοδιανυσμάτων πίνακα, στην προκειμένη περίπτωση Χαμιλτονιανού πίνακα:
Ηci = Ei ci (8)
Γενικά για τα μόρια η επίλυση της εξίσωσης του Schroedinger παραμένει ένα
δύσκολο πρόβλημα. Είναι συνήθως χρήσιμο στη Χημεία να εισαγάγουμε υποθέσεις
που ισχύουν για ορισμένες κατηγορίες μορίων, τέτοιες που κάνουν την εύρεση
των μοριακών τροχιακών, όπως ονομάζονται οι ιδιοσυναρτήσεις και
των αντίστοιχων ιδιοενεργειών τους εφικτή για μικρού μεγέθους Η/Υ.
Μια τέτοια μέθοδος είναι αυτή του Huckel
για συστήματα με μοριακά τρχιακά τύπου π.