Further Details: Error Bounds for Linear Least Squares Problems

The conventional error analysis of linear least squares problems goes as follows. As above, let $\hat{x}$ be the solution to minimizing $\Vert Ax-b \Vert _2$ computed by LAPACK using one of the least squares drivers xGELS, xGELSX, xGELSY, xGELSS or xGELSD (see subsection 2.3.2). We discuss the most common case, where A is overdetermined (i.e., has more rows than columns) and has full rank [16,25,55,67]:

The computed solution $\hat{x}$ has a small normwise backward error. In other words $\hat{x}$ minimizes $\Vert(A+E) \hat{x}- (b+f)\Vert _2$, where E and f satisfy

$$\max \left( \frac{\Vert E \Vert _2}{\Vert A \Vert _2} , \frac{\Vert f \Vert _2}{\Vert b \Vert _2} \right) \leq p(n) \epsilon$$

and p(n) is a modestly growing function of n. We take p(n)=1 in the code fragments above. Let $\kappa_2 (A) = \sigma_{\max} (A)/\sigma_{\min} (A)$ (approximated by 1/RCOND in the above code fragments), $\rho = \Vert A \hat{x} -b\Vert _2$ (= RNORM above), and $\sin ( \theta ) = \rho / \Vert b\Vert _2$ (SINT = RNORM / BNORM above). Here, $\theta$ is the acute angle between the vectors $A \hat{x}$ and b. Then when $p(n) \epsilon$ is small, the error $\hat{x}- x$ is bounded by

$$\frac{\Vert x-\hat{x}\Vert _2}{\Vert x\Vert _2} \mathrel{\ra... ...)}{\cos ( \theta )} + \tan ( \theta ) \kappa_2^2 (A) \right\},$$

where $\cos ( \theta )$ = COST and $\tan ( \theta )$ = TANT in the code fragments above.

We avoid overflow by making sure RCOND and COST are both at least $\epsilon =$ EPSMCH, and by handling the case of a zero B matrix separately (BNORM = 0).

$\kappa_2 (A) = \sigma_{\max} (A)/\sigma_{\min} (A)$ may be computed directly from the singular values of A returned by xGELSS or xGELSD (as in the code fragment) or by xGESVD or xGESDD. It may also be approximated by using xTRCON following calls to xGELS, xGELSX or xGELSY. xTRCON estimates $\kappa_{\infty}$ or $\kappa_1$ instead of $\kappa_2$, but these can differ from $\kappa_2$ by at most a factor of n.

If A is rank-deficient, xGELSS, xGELSD, xGELSY and xGELSX can be used to regularize the problem by treating all singular values less than a user-specified threshold ( ${\tt RCND} \cdot \sigma_{\max} (A)$) as exactly zero. The number of singular values treated as nonzero is returned in RANK. See [16,55,67] for error bounds in this case, as well as [28] for the underdetermined case. The ability to deal with rank-deficient matrices is the principal attraction of these four drivers, which are more expensive than the simple driver xGELS.

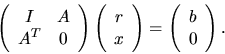
The solution of the overdetermined, full-rank problem may also be characterized as the solution of the linear system of equations

$$\left( \begin{array}{cc} I & A \\ A^T & 0 \end{array} \right... ...\right) = \left( \begin{array}{c} b \\ 0 \end{array} \right) .$$

By solving this linear system using xyyRFS or xyySVX (see section 4.4) componentwise error bounds can also be obtained [7].