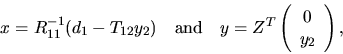Generalized QR Factorization

The generalized QR (GQR) factorization of an n-by-m matrix A and an n-by-p matrix B is given by the pair of factorizations

$$A = Q R \quad \mbox{and} \quad B = Q T Z$$

where Q and Z are respectively n-by-n and p-by-p orthogonal matrices (or unitary matrices if A and B are complex). R has the form:

$$R = \bordermatrix{ & m \cr \hfill m & R_{11} \cr n-m & 0 }, \quad \mbox{if} \quad n \geq m$$

or

$$R = \bordermatrix{ & n & m-n \cr n & R_{11} & R_{12} }, \quad \mbox{if} \quad n < m$$

where R₁₁ is upper triangular. T has the form

$$T = \bordermatrix{ & p-n & n \cr n & 0 & T_{12} }, \quad \mbox{if} \quad n \leq p$$

or

$$T = \bordermatrix{ & p \cr n-p & T_{11} \cr \hfill p & T_{21} }, \quad \mbox{if} \quad n > p$$

where T₁₂ or T₂₁ is upper triangular.

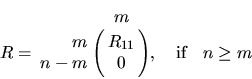
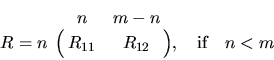
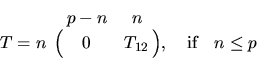
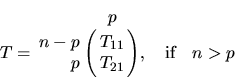
Note that if B is square and nonsingular, the GQR factorization of A and B implicitly gives the QR factorization of the matrix B^-1A:

B^-1 A = Z^T ( T^-1 R )

without explicitly computing the matrix inverse B^-1 or the product B^-1A.

The routine xGGQRF computes the GQR factorization by first computing the QR factorization of A and then the RQ factorization of Q^TB. The orthogonal (or unitary) matrices Q and Z can either be formed explicitly or just used to multiply another given matrix in the same way as the orthogonal (or unitary) matrix in the QR factorization (see section 2.4.2).

The GQR factorization was introduced in [60,84]. The implementation of the GQR factorization here follows [2]. Further generalizations of the GQR factorization can be found in [22].

The GQR factorization can be used to solve the general (Gauss-Markov) linear model problem (GLM) (see (2.3) and [81][55, page 252]). Using the GQR factorization of A and B, we rewrite the equation d = A x + B y from (2.3) as

$$\begin{eqnarray*} Q^T d & = & Q^T A x + Q^T B y \\ & = & R x + T Z y. \end{eqnarray*}$$

We partition this as

$$\left( \begin{array}{c} d_1 \\ d_2 \end{array} \right) =... ...left( \begin{array}{c} y_1 \\ y_2 \\ \end{array} \right)$$

where

$$\left( \begin{array}{c} d_1 \\ d_2 \\ \end{array} \righ... ...ray}{c} y_1 \\ y_2 \\ \end{array} \right) \equiv Z y \; ;$$

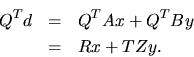
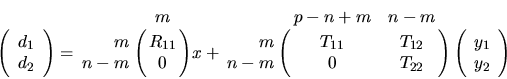
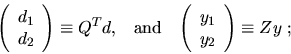
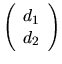$\left( \begin{array}{c} d_1 \\ d_2 \end{array} \right)$ can be computed by xORMQR (or xUNMQR).

The GLM problem is solved by setting

$$y_1 = 0 \quad \mbox{and} \quad y_2 = T^{-1}_{22} d_2$$

from which we obtain the desired solutions

$$x = R^{-1}_{11}(d_1 - T_{12} y_2) \quad \mbox{and} \quad y =... ...\left( \begin{array}{c} 0 \\ y_2 \\ \end{array} \right) ,$$

which can be computed by xTRSV, xGEMV and xORMRQ (or xUNMRQ).