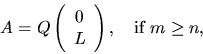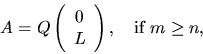Next: Generalized Orthogonal Factorizations and
Up: Orthogonal Factorizations and Linear
Previous: Complete Orthogonal Factorization
Contents
Index
The QL and RQ factorizations
are given by
and
These factorizations are computed by xGEQLF and xGERQF, respectively; they are
less commonly used than either the QR or LQ factorizations
described above, but have applications in, for example, the
computation of generalized QR factorizations [2].
All the factorization routines discussed here (except xTZRQF and xTZRZF) allow
arbitrary m and n, so that in some cases the matrices R or L are
trapezoidal rather than triangular.
A routine that performs pivoting is provided only for the QR factorization.
Table 2.9:
Computational routines for orthogonal factorizations
| Type of factorization |
Operation |
Single precision |
Double precision |
| and matrix |
|
real |
complex |
real |
complex |
| QR, general |
factorize with pivoting |
SGEQP3 |
CGEQP3 |
DGEQP3 |
ZGEQP3 |
| |
factorize, no pivoting |
SGEQRF |
CGEQRF |
DGEQRF |
ZGEQRF |
| |
generate Q |
SORGQR |
CUNGQR |
DORGQR |
ZUNGQR |
| |
multiply matrix by Q |
SORMQR |
CUNMQR |
DORMQR |
ZUNMQR |
| LQ, general |
factorize, no pivoting |
SGELQF |
CGELQF |
DGELQF |
ZGELQF |
| |
generate Q |
SORGLQ |
CUNGLQ |
DORGLQ |
ZUNGLQ |
| |
multiply matrix by Q |
SORMLQ |
CUNMLQ |
DORMLQ |
ZUNMLQ |
| QL, general |
factorize, no pivoting |
SGEQLF |
CGEQLF |
DGEQLF |
ZGEQLF |
| |
generate Q |
SORGQL |
CUNGQL |
DORGQL |
ZUNGQL |
| |
multiply matrix by Q |
SORMQL |
CUNMQL |
DORMQL |
ZUNMQL |
| RQ, general |
factorize, no pivoting |
SGERQF |
CGERQF |
DGERQF |
ZGERQF |
| |
generate Q |
SORGRQ |
CUNGRQ |
DORGRQ |
ZUNGRQ |
| |
multiply matrix by Q |
SORMRQ |
CUNMRQ |
DORMRQ |
ZUNMRQ |
| RZ, trapezoidal |
factorize, no pivoting |
STZRZF |
CTZRZF |
DTZRZF |
ZTZRZF |
| |
(blocked algorithm) |
|
|
|
|
| |
multiply matrix by Q |
SORMRZ |
CUNMRZ |
DORMRZ |
ZUNMRZ |





Next: Generalized Orthogonal Factorizations and
Up: Orthogonal Factorizations and Linear
Previous: Complete Orthogonal Factorization
Contents
Index
Susan Blackford
1999-10-01