Implementation

deriv_class is a collection of functions overloading all operators and all appropriate FORTRAN 90 functions and subroutines to accept not only real values but also variables of a derived type (TYPE (func)) comprised of the value, the first and the second derivatives of the corresponding mathematical quantity.

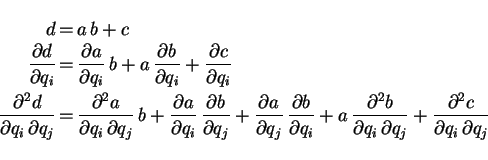
The compiler is ``taught'' how to handle expressions involving variables of this type--addition, subtraction, multiplication, etc. between them--and, also, how to apply all meaningful FORTRAN 90 functions and subroutines on them in order to compute not only the value of the expression but, in addition, the numerical value of the first and second derivatives. deriv_class also provides functions to interpret mixed mode expressions between variables of TYPE (func), reals, and integers. Using this module, the compiler is able to apply the usual rules of differentiation (including the chain rule for cumbersome expressions) on any statement. That is, the compiler parsing a statement involving the TYPE (func) variables a,b,c,d like

d = a * b + c

will generate a code to evaluate the following mathematical expressions:

$$\begin{eqnarray*} d &=& a\, b + c \\ \frac{\partial d}{\partial q_i} &=& \fra... ...partial q_j} + \frac{\partial^2 c}{\partial q_i\,\partial q_j} \end{eqnarray*}$$

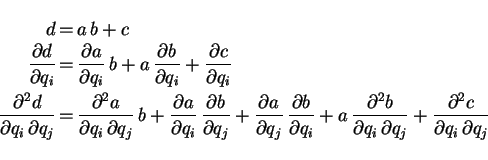
Allocatable components of a derived type are not yet part of FORTRAN. It is necessary, therefore, to define prior to compiling, the number of independent variables (in the mathematical sense); n is the integer which holds it.

The components of a TYPE (func) variable are a REAL variable for the value (value) of the function, and two rank-1 arrays of n and $n\,(n + 1) / 2$ REAL elements (x, xx), for the first and second derivatives, respectively. The arrays hold the gradient and the upper triangle of the Hessian; it is stored in the format:

$$xx(i + n\,(j - 1) - j\,(j - 1) / 2) = H_{ji}\;\;(i \ge j).$$ (1)

A few parameters are defined in the module; they are the kind of the components of TYPE (func), (dpk), and the kind for the reals (spk) and the integers (ik) that can appear in the same expression. Currently, FORTRAN provides no mechanism to utilize implicit promotions in expressions involving derived types or define conversions of one derived type to another. It was necessary, therefore, to write all procedures into supported types.

The default values for the kinds yield double precision, default real, and default integer numbers. They can be tailored to extend the precision. Note, however, that dpk, and spk must correspond to different precisions to avoid clashes in overloading resolution. The FORTRAN 90 standard ensures that at least two different kinds of reals are provided by the compiler. Multiple definitions of these kinds can be eliminated by modifying the module to inherit the kinds from another or export them outside deriv_class by changing the access attribute. By default, these and all ``internal'' variables and functions are of PRIVATE access.

Note, that complex variables are not supported.

There is a number of variables to be specified at run-time, before the computation is enabled. These are the required order of differentiation (drvtv) and the independent variables. Two subroutines are provided, derivative and independent, to manipulate them from the user's routine.

The subroutine derivative accepts an integer argument and assigns it to drvtv. It should be either 0, 1 or 2. All derivatives with order less or equal to this number will be evaluated (considering the value of the function as the zeroth derivative). An argument different than 0, 1 or 2 results in computing only the value. The interface is:

  SUBROUTINE derivative(der)
    INTEGER, INTENT (in) :: der
  END SUBROUTINE derivative

The subroutine independent is used for declaring a TYPE (func) variable as mathematically independent. The routine accepts three arguments, the variable, a REAL (dpk) value and an integer i. It zeroes the derivatives of the independent variable except the i^th component of the first derivative, which is set to unity. It also assigns to the appropriate component of the TYPE (func) variable the supplied real value. This routine should be repeatedly called for all independent variables. Its interface is:

    SUBROUTINE independent(i, x, val)
      INTEGER, INTENT (in) :: i
      TYPE (func), INTENT (out) :: x
      REAL (dpk), INTENT (in) :: val
    END SUBROUTINE independent

The module deriv_class provides the subroutine extract to ``decode'' a TYPE (func) variable. It breaks it up into a real number (for the value), and two optional rank-1 arrays for the derivatives. There is a number of routines to extract them separately (under the generic names value, FD, SD) but normally they need not be used; therefore, they are private to the module. The interface of extract is:

  SUBROUTINE extract(x, val, Dx, DDx)
    TYPE (func), INTENT (in) :: x
    REAL (dpk), INTENT (out) :: val
    REAL (dpk), INTENT (out), OPTIONAL :: Dx(n), DDx(n*(n+1)/2)
  END SUBROUTINE extract