There are three types of problems to consider.
In all cases A and B
are real symmetric (or complex Hermitian) and B is positive definite.
These decompositions are computed for real symmetric matrices
by the driver routines
xSYGV, xSYGVX, xSYGVD,
xSPGV, xSPGVX, xSPGVD,
and (for type 1 only)
xSBGV, xSBGVX and xSBGVD
(see subsection 2.3.5.1).
These decompositions are computed for complex Hermitian matrices
by the driver routines
xHEGV, xHEGVX, xHEGVD,
xHPGV, xHPGVX, xHPGVD,
and (for type 1 only)
xHBGV, xHBGVX, xHBGVD
(see subsection 2.3.5.1).
In each of the following three decompositions,
![]() is real and diagonal with diagonal entries
is real and diagonal with diagonal entries
![]() ,
and
the columns zi of Z are linearly independent vectors.
The
,
and
the columns zi of Z are linearly independent vectors.
The ![]() are called
eigenvalues and the zi are
eigenvectors.
are called
eigenvalues and the zi are
eigenvectors.
The approximate error bounds4.10for the computed eigenvalues
![]() are
are
EPSMCH = SLAMCH( 'E' )
* Solve the eigenproblem A - lambda B (ITYPE = 1)
ITYPE = 1
* Compute the norms of A and B
ANORM = SLANSY( '1', UPLO, N, A, LDA, WORK )
BNORM = SLANSY( '1', UPLO, N, B, LDB, WORK )
* The eigenvalues are returned in W
* The eigenvectors are returned in A
CALL SSYGV( ITYPE, 'V', UPLO, N, A, LDA, B, LDB, W, WORK,
$ LWORK, INFO )
IF( INFO.GT.0 .AND. INFO.LE.N ) THEN
PRINT *,'SSYGV did not converge'
ELSE IF( INFO.GT.N ) THEN
PRINT *,'B not positive definite'
ELSE IF ( N.GT.0 ) THEN
* Get reciprocal condition number RCONDB of Cholesky factor of B
CALL STRCON( '1', UPLO, 'N', N, B, LDB, RCONDB, WORK, IWORK,
$ INFO )
RCONDB = MAX( RCONDB, EPSMCH )
CALL SDISNA( 'Eigenvectors', N, N, W, RCONDZ, INFO )
DO 10 I = 1, N
EERRBD( I ) = ( EPSMCH / RCONDB**2 ) * ( ANORM / BNORM +
$ ABS( W(I) ) )
ZERRBD( I ) = ( EPSMCH / RCONDB**3 ) * ( ( ANORM / BNORM )
$ / RCONDZ(I) + ( ABS( W(I) ) / RCONDZ(I) ) *
$ RCONDB )
10 CONTINUE
END IF
For example4.11, if
![]() ,
,
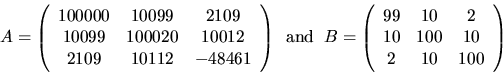
| i | EERRBD(i) | true
|
ZERRBD(i) | true
|
|
| 1 | -500.0 |
|
|
|
|
| 2 | 1000. |
|
|
|
|
| 3 | 1010. |
|
|
|
|
This code fragment cannot be adapted to use xSBGV (or xHBGV), because xSBGV does not return a conventional Cholesky factor in B, but rather a ``split'' Cholesky factorization (performed by xPBSTF).
EPSMCH = SLAMCH( 'E' )
* Solve the eigenproblem A*B - lambda I (ITYPE = 2)
ITYPE = 2
* Compute the norms of A and B
ANORM = SLANSY( '1', UPLO, N, A, LDA, WORK )
BNORM = SLANSY( '1', UPLO, N, B, LDB, WORK )
* The eigenvalues are returned in W
* The eigenvectors are returned in A
CALL SSYGV( ITYPE, 'V', UPLO, N, A, LDA, B, LDB, W, WORK,
$ LWORK, INFO )
IF( INFO.GT.0 .AND. INFO.LE.N ) THEN
PRINT *,'SSYGV did not converge'
ELSE IF( INFO.GT.N ) THEN
PRINT *,'B not positive definite'
ELSE IF ( N.GT.0 ) THEN
* Get reciprocal condition number RCONDB of Cholesky factor of B
CALL STRCON( '1', UPLO, 'N', N, B, LDB, RCONDB, WORK, IWORK,
$ INFO )
RCONDB = MAX( RCONDB, EPSMCH )
CALL SDISNA( 'Eigenvectors', N, N, W, RCONDZ, INFO )
DO 10 I = 1, N
EERRBD(I) = ( ANORM * BNORM ) * EPSMCH +
$ ( EPSMCH / RCONDB**2 ) * ABS( W(I) )
ZERRBD(I) = ( EPSMCH / RCONDB ) * ( ( ANORM * BNORM ) /
$ RCONDZ(I) + 1.0 / RCONDB )
10 CONTINUE
END IF
For the same A and B as above, the approximate eigenvalues, approximate error bounds, and true errors are
| i | EERRBD(i) | true
|
ZERRBD(i) | true
|
|
| 1 |
|
1.3 |
|
|
|
| 2 |
|
1.6 | 1.5 |
|
|
| 3 |
|
1.9 | 4.5 |
|
|