Error Bounds for the Nonsymmetric Eigenproblem

The nonsymmetric eigenvalue problem is more complicated than the symmetric eigenvalue problem. In this subsection, we state the simplest bounds and leave the more complicated ones to subsequent subsections.

Let A be an n-by-n nonsymmetric matrix, with eigenvalues $\lambda_1, \ldots , \lambda_n$. Let v_i be a right eigenvector corresponding to $\lambda_i$: $A v_i = \lambda_i v_i$. Let $\hat{\lambda}_i$ and $\hat{v}_i$ be the corresponding computed eigenvalues and eigenvectors, computed by expert driver routine xGEEVX (see subsection 2.3.4).

The approximate error bounds^4.10for the computed eigenvalues are

$$\vert \hat{\lambda}_i - \lambda_i \vert \leq {\tt EERRBD}(i) \; \; .$$

The approximate error bounds for the computed eigenvectors $\hat{v}_i$, which bound the acute angles between the computed eigenvectors and true eigenvectors v_i, are

$$\theta ( \hat{v}_i , v_i ) \leq {\tt VERRBD}(i) \; .$$

These bounds can be computed by the following code fragment:

      EPSMCH = SLAMCH( 'E' )
*     Compute the eigenvalues and eigenvectors of A
*     WR contains the real parts of the eigenvalues
*     WI contains the real parts of the eigenvalues
*     VL contains the left eigenvectors
*     VR contains the right eigenvectors
      CALL SGEEVX( 'P', 'V', 'V', 'B', N, A, LDA, WR, WI,
     $             VL, LDVL, VR, LDVR, ILO, IHI, SCALE, ABNRM,
     $             RCONDE, RCONDV, WORK, LWORK, IWORK, INFO )
      IF( INFO.GT.0 ) THEN
         PRINT *,'SGEEVX did not converge'
      ELSE IF ( N.GT.0 ) THEN
         DO 10 I = 1, N
            EERRBD(I) = EPSMCH*ABNRM/RCONDE(I)
            VERRBD(I) = EPSMCH*ABNRM/RCONDV(I)
10       CONTINUE
      ENDIF

For example^4.11, if ${\tt SLAMCH('E')} = 2^{-24} = 5.961 \cdot 10^{-8}$ and

$$A = \left( \begin{array}{ccc} 58 & 9 & 2 \\ 186 & 383 & 96 \\ -912 & -1551 & -388 \end{array} \right)$$

then true eigenvalues, approximate eigenvalues, approximate error bounds, and true errors are

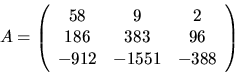
i	$\lambda_i$	$\hat{\lambda}_i$	EERRBD(i)	true $\vert \hat{\lambda}_i - \lambda_i \vert$	VERRBD(i)	true $\theta ( \hat{v}_i , v_i )$
1	50	50.00	$8.5 \cdot 10^{-4}$	$2.7 \cdot 10^{-4}$	$2.6 \cdot 10^{-5}$	$8.5 \cdot 10^{-6}$
2	2	1.899	$3.1 \cdot 10^{-1}$	$1.0 \cdot 10^{-1}$	$1.9 \cdot 10^{-4}$	$7.7 \cdot 10^{-5}$
3	1	1.101	$3.1 \cdot 10^{-1}$	$1.0 \cdot 10^{-1}$	$1.8 \cdot 10^{-4}$	$7.5 \cdot 10^{-5}$