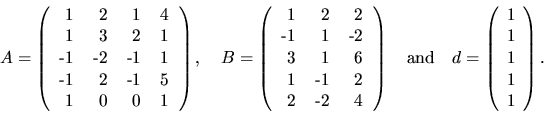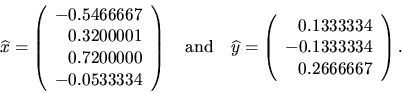General Linear Model Problem

The general linear model (GLM) problem is

$$\min_{x,y} \Vert y\Vert \quad \mbox{subject to} \quad d = Ax + By$$

where A is an n-by-m matrix, B is an n-by-p matrix, and d is a given n-vector, with $m \leq n \leq m+p$.

The GLM problem is solved by the driver routine xGGGLM (see section 4.6). Let $\widehat {x}$ and $\widehat {y}$ be the computed values of x and y, respectively. The approximate error bounds

$$\begin{eqnarray*} % latex2html id marker 11027\frac{ \Vert x - \widehat {x} \... ...hfil ...$$

can be computed by the following code fragment

      EPSMCH = SLAMCH( 'E' )
*     Compute the 2-norm of the left hand side D
      DNORM = SNRM2( N, D, 1 )
*     Solve the generalized linear model problem
      CALL SGGGLM( N, M, P, A, LDA, B, LDB, D, Xc, Yc, WORK,
     $            LWORK, IWORK, INFO )
*     Compute the F-norm of A and B
      ANORM = SLANTR( 'F', 'U', 'N', M, M, A, LDA, WORK( M+NP+1 ) )
      BNORM = SLANTR( 'F', 'U', 'N', N, P, B( 1, MAX( 1, P-N+1 ) ),
     $                LDB, WORK( M+NP+1 ) )
*     Compute the 2-norm of Xc
      XNORM = SNRM2( M, Xc, 1 )
*     Condition estimation
      IF( N.EQ.M ) THEN
         PBPSNM = ZERO
         TNORM = SLANTR( '1', 'U', 'N', N, N, A, LDA, WORK( M+NP+M+1 ) )
         CALL STRCON( '1', 'U', 'N', N, A, LDA, RCOND, WORK( M+NP+M+1 ),
     $                IWORK, INFO )
         ABPSNM = ONE / (RCOND * TNORM )
      ELSE
*        Compute norm of (PB)^+
         TNORM = SLANTR( '1', 'U', 'N', N-M, N-M, B( M+1, P-N+M+1 ), LDB,
     $                   WORK( M+NP+1 ) )
         CALL STRCON( '1', 'U', 'N', N-M, B( M+1, P-N+M+1 ), LDB, RCOND,
     $                WORK( M+NP+1 ), IWORK, INFO )
         PBPSNM = ONE / (RCOND * TNORM )
*        Estimate norm of A^+_B
         KASE = 0
         CALL SLACON( N, WORK( M+NP+1 ), WORK( M+NP+N+1 ), IWORK, EST, KASE )
   30    CONTINUE
            CALL STRSV( 'Upper', 'No transpose', 'Non unit', N-M,
     $                  B( M+1, P-N+M+1 ), LDB, WORK( M+NP+N+M+1 ), 1 )
            CALL SGEMV( 'No transpose', M, N-M, -ONE, B( 1, P-N+M+1 ),
     $                  LDB, WORK( M+NP+N+M+1 ), 1, ONE,
     $                  WORK( M+NP+N+1 ), 1 )
            CALL STRSV( 'Upper', 'No transpose', 'Non unit', M, A, LDA,
     $                  WORK( M+NP+N+1 ), 1 )
            DO I = 1, P
               WORK( M+NP+I ) = WORK( M+NP+N+I )
            END DO
            CALL SLACON( M, WORK( M+NP+N+1 ), WORK( M+NP+1 ), IWORK, EST, KASE )
            IF( KASE.EQ.0 ) GOTO 40
            CALL STRSV( 'Upper', 'Transpose', 'Non unit', M, A, LDA,
     $                  WORK( M+NP+1 ), 1 )
            CALL SGEMV( 'Transpose', M, N-M, -ONE, B( 1, P-N+M+1 ), LDB,
     $                  WORK( M+NP+1 ), 1, ZERO, WORK( M+NP+M+1 ), 1 )
            CALL STRSV( 'Upper', 'Transpose', 'Non unit', N-M,
     $                  B( M+1, P-N+M+1 ), LDB, WORK( M+NP+M+1 ), 1 )
            DO I = 1, N
               WORK( M+NP+N+I ) = WORK( M+NP+I )
            END DO
            CALL SLACON( N, WORK( M+NP+1 ), WORK( M+NP+N+1 ), IWORK, EST, KASE )
            IF( KASE.EQ.0 ) GOTO 40
         GOTO 30
   40    CONTINUE
         ABPSNM = EST
      END IF
*     Estimate norm of (A^+_B)*B
      IF( P+M.EQ.N ) THEN
         EST = ZERO
      ELSE
         KASE = 0
         CALL SLACON( P-N+M, WORK( M+NP+1 ), WORK( M+NP+M+1 ), IWORK, EST, KASE )
   50    CONTINUE
*
            IF( P.GE.N ) THEN
               CALL STRMV( 'Upper', 'No trans', 'Non Unit', M,
     $                     B( 1, P-N+1 ), LDB, WORK( M+NP+M+P-N+1 ), 1 )
               DO I = 1, M
                  WORK( M+NP+I ) = WORK( M+NP+M+P-N+I )
               END DO
            ELSE
               CALL SGEMV( 'No transpose', N-P, P-N+M, ONE, B, LDB,
     $                  WORK( M+NP+M+1 ), 1, ZERO, WORK( M+NP+1 ), 1 )
               CALL STRMV( 'Upper', 'No trans', 'Non Unit', P-N+M,
     $                     B( N-P+1, 1 ), LDB, WORK( M+NP+M+1 ), 1 )
               DO I = N-P+1, M
                  WORK( M+NP+I ) = WORK( M+NP+M-N+P+I )
               END DO
            END IF
            CALL STRSV( 'Upper', 'No transpose', 'Non unit', M, A, LDA,
     $                  WORK( M+NP+1 ), 1 )
            CALL SLACON( M, WORK( M+NP+M+1 ), WORK( M+NP+1 ), IWORK, EST, KASE )
*
            IF( KASE.EQ.0 ) GOTO 60
*
            CALL STRSV( 'Upper', 'Transpose', 'Non unit', M, A, LDA,
     $                  WORK( M+NP+1 ), 1 )
            IF( P.GE.N ) THEN
               CALL STRMV( 'Upper', 'Trans', 'Non Unit', M,
     $                     B( 1, P-N+1 ), LDB, WORK( M+NP+1 ), 1 )
               DO I = 1, M
                  WORK( M+NP+M+P-N+I ) = WORK( M+NP+I )
               END DO
               DO I = 1, P-N
                  WORK( M+NP+M+I ) = ZERO
               END DO
            ELSE
               CALL STRMV( 'Upper', 'Trans', 'Non Unit', P-N+M,
     $                     B( N-P+1, 1 ), LDB, WORK( M+NP+N-P+1 ), 1 )
               DO I = 1, P-N+M
                  WORK( M+NP+M+I ) = WORK( M+NP+N-P+I )
               END DO
               CALL SGEMV( 'Transpose', N-P, P-N+M, ONE, B, LDB,
     $                  WORK( M+NP+1 ), 1, ONE, WORK( M+NP+M+1 ), 1 )
            END IF
            CALL SLACON( P-N+M, WORK( M+NP+1 ), WORK( M+NP+M+1 ), IWORK, EST,
     $                   KASE )
*
            IF( KASE.EQ.0 ) GOTO 60
         GOTO 50
   60    CONTINUE
      END IF
      ABPSBN = EST
*     Get condition numbers and approximate error bounds
      CNDAB = ANORM*ABPSNM
      CNDBA = BNORM*PBPSNM
      IF( PBPSNM.EQ.0.0E+0 ) THEN
*        Then A is square and nonsingular
         XERRBD = EPSMCH*( CNDAB*( ONE+DNORM/(ANORM*XNORM) ) )
         YERRBD = 0.0E+0
      ELSE
         XERRBD = EPSMCH*( CNDAB*( ONE+DNORM/(ANORM*XNORM) ) +
     $                2.0E0*CNDAB*CNDBA*CNDBA*DNORM/(ANORM*XNORM) +
     $                ABPSBN*ABPSBN*PBPSNM*PBPSNM*ANORM*DNORM/XNORM )
         YERRBD = EPSMCH*( ABPSBN*ANORM*PBPSNM*PBPSNM +
     $                PBPSNM*(ANORM*XNORM/DNORM + 2.0E0*CNDBA*CNDBA +
     $                ONE) + CNDBA*PBPSNM )
      END IF

For example, if ${\tt SLAMCH('E')} = 2^{-24} = 5.961 \cdot 10^{-8}$,

$$A = \left( \begin{tabular}{rrrr} 1 & 2 & 1 & 4 \\ 1 & 3 & ... ...array}{r} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{array} \right).$$

Then (to 7 decimal places)

$$\widehat {x} = \left( \begin{array}{r} -0.5466667 \\ 0.320... ... 0.1333334 \\ -0.1333334 \\ 0.2666667 \end{array} \right).$$

The computed error bounds ${\tt XERRBD} = 1.2\cdot10^{-5}$ and ${\tt YERRBD} = 6.4\cdot10^{-7}$, where ${\tt CNDAB} = 26.97$, ${\tt CNDBA} = 1.78$, The true errors in x and y are $1.2\cdot10^{-7}$ and $1.3\cdot10^{-7}$, respectively. Note that the exact solutions are $x = \frac{1}{75}[-41,24,54,-4]^T$ and $y = \frac{1}{15}[2,-2,4]^T$.