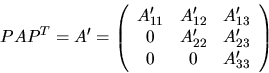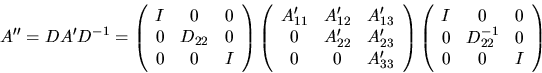Balancing

The routine xGEBAL may be used to balance the matrix A prior to reduction to Hessenberg form. Balancing involves two steps, either of which is optional:

• first, xGEBAL attempts to permute A by a similarity transformation to block upper triangular form:
  
  $$P A P^T = A' = \left( \begin{array}{ccc} A'_{11} & A'_{12} ... ...0 & A'_{22} & A'_{23} \\ 0 & 0 & A'_{33} \end{array} \right)$$
  
  
  where P is a permutation matrix and A'₁₁ and A'₃₃ are upper triangular. Thus the matrix is already in Schur form outside the central diagonal block A'₂₂ in rows and columns ILO to IHI. Subsequent operations by xGEBAL, xGEHRD or xHSEQR need only be applied to these rows and columns; therefore ILO and IHI are passed as arguments to xGEHRD and xHSEQR. This can save a significant amount of work if ILO > 1 or IHI < n. If no suitable permutation can be found (as is very often the case), xGEBAL sets ILO = 1 and IHI = n, and A'₂₂ is the whole of A.

• secondly, xGEBAL applies a diagonal similarity transformation to A' to make the rows and columns of A'₂₂ as close in norm in possible:
  
  $$A'' = D A' D^{-1} = \left( \begin{array}{ccc} I & 0 & 0 \\ ... ... 0 \\ 0 & D_{22}^{-1} & 0 \\ 0 & 0 & I \end{array} \right)$$
  
  
  This can improve the accuracy of later processing in some cases; see subsection 4.8.1.2.

If A was balanced by xGEBAL, then eigenvectors computed by subsequent operations are eigenvectors of the balanced matrix A''; xGEBAK must then be called to transform them back to eigenvectors of the original matrix A.