| Routine |
Description |
| real |
complex |
|
| SSPCON |
CSPCON CHPCON |
Estimates the reciprocal of the condition number of
a real symmetric/complex symmetric/complex Hermitian indefinite matrix in
packed storage,
using the factorization computed by SSPTRF/CSPTRF/CHPTRF. |
| SSPEV |
CHPEV |
Computes all eigenvalues and, optionally, eigenvectors of
a symmetric/Hermitian matrix in packed storage. |
| SSPEVD |
CHPEVD |
Computes all eigenvalues and, optionally, eigenvectors of
a symmetric/Hermitian matrix in packed storage. If eigenvectors are
desired, it uses a divide and conquer algorithm. |
| SSPEVX |
CHPEVX |
Computes selected eigenvalues and eigenvectors of
a symmetric/Hermitian matrix in packed storage. |
| SSPGST |
CHPGST |
Reduces a symmetric/Hermitian definite generalized eigenproblem
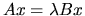 , ,
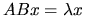 ,
or ,
or 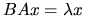 ,
to standard form,
where A and B are held in packed storage,
and B has been factorized by SPPTRF/CPPTRF. ,
to standard form,
where A and B are held in packed storage,
and B has been factorized by SPPTRF/CPPTRF. |
| SSPGV |
CHPGV |
Computes all eigenvalues and optionally, the eigenvectors of
a generalized symmetric/Hermitian definite generalized eigenproblem,
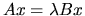 , ,
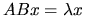 ,
or ,
or 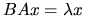 ,
where A and B are in packed storage. ,
where A and B are in packed storage. |
| SSPGVD |
CHPGVD |
Computes all eigenvalues, and optionally, the eigenvectors of
a generalized symmetric/Hermitian definite generalized eigenproblem,
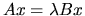 , ,
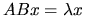 ,
or ,
or 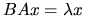 ,
where A and B are in packed storage. If eigenvectors are
desired, it uses a divide and conquer algorithm. ,
where A and B are in packed storage. If eigenvectors are
desired, it uses a divide and conquer algorithm. |
| SSPGVX |
CHPGVX |
Computes selected eigenvalues, and optionally, the eigenvectors of
a generalized symmetric/Hermitian definite generalized eigenproblem,
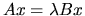 , ,
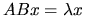 ,
or ,
or 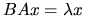 ,
where A and B are in packed storage. ,
where A and B are in packed storage. |
| SSPRFS |
CSPRFS CHPRFS |
Improves the computed solution to
a real symmetric/complex symmetric/complex Hermitian indefinite system of linear
equations
A X=B,
where A is held in packed storage,
and provides forward and backward error bounds for the solution. |
| SSPSV |
CSPSV CHPSV |
Solves a real symmetric/complex symmetric/complex Hermitian indefinite system
of linear equations
A X=B,
where A is held in packed storage. |
| SSPSVX |
CSPSVX CHPSVX |
Solves a real symmetric/complex symmetric/complex Hermitian indefinite system
of linear equations
A X=B,
where A is held in packed storage,
and provides an estimate of the condition number
and error bounds on the solution. |
| SSPTRD |
CHPTRD |
Reduces a symmetric/Hermitian matrix in packed storage
to real symmetric tridiagonal form
by an orthogonal/unitary similarity transformation. |