ΤΑΥΤΟΠΟΙΗΣΗ ΜΟΡΙΑΚΩΝ ΕΙΔΩΝ ΜΕ ΤΗΝ ΦΑΣΜΑΤΟΣΚΟΠΙΑ RAMAN

ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗS

ΤΜΗΜΑ XΗΜΕΙΑS

ΕΠΕΑΕΚ ΠΜΣ

ΕΦΗΡΜΟΣΜΕΝΗ ΜΟΡΙΑΚΗ ΦΑΣΜΑΤΟΣΚΟΠΙΑ

Υπεύθυνος εργου: καθ. Σταύρος Κ. Φαράντος

ΣΤΟΙΧΕΙΑ ΦΑΣΜΑΤΟΣΚΟΠΙΑΣ RAMAN

Γ. Βογιατζής, Σ. Γιαννόπουλος & Γ. Παπαθεοδώρου

ΙΔΡΥΜΑ ΤΕΧΝΟΛΟΓΙΑΣ & ΕΡΕΥΝΑΣ

ΕΡΕΥΝΗΤΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΥΨΗΛΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ

&

ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ

ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ

ΔΕΚΕΜΒΡΙΟΣ 1999

ΑΣΚΗΣΗ 1

EΙΣΑΓΩΓΉ ΣΤΗΝ ΦΑΣΜΑΤΟΣΚΟΠΙΑ RAMAN

ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ

Α. Εισαγωγή

Η σκέδαση Raman είναι ένα από τα φαινόμενα που προκύπτουν από την αλληλεπίδραση ακτινοβολίας και ύλης. Ένα χαρακτηριστικό γνώρισμα της σκέδασης Raman είναι η αλλαγή στην συχνότητα του σκεδαζόμενου φωτός, η συχνότητα δηλαδή της σκεδαζόμενης ακτινοβολίας είναι διαφορετική από αυτήν της προσπίπτουσας.

Σε μια πρώτη προσέγγιση είναι δυνατόν να θεωρηθεί ότι η ενέργεια ενός μορίου μπορεί να χωριστεί σε τρεις συνιστώσες: (α) την περιστροφή του μορίου σαν σύνολο, (β) τις δονήσεις των ατόμων που το αποτελούν και (γ) την κίνηση των ηλεκτρονίων του. Η μεταφορική ενέργεια του μορίου σχετίζεται με άλλα φαινόμενα που δεν αποτελούν αντικείμενο της άσκησης αυτής. Ένας διαχωρισμός σαν και αυτόν που αναφέρθηκε προκύπτει από την παρατήρηση ότι η κίνηση των ηλεκτρονίων είναι αρκετά πιο γρήγορη από την κίνηση δόνησης των πυρήνων και η τελευταία είναι επίσης πιο γρήγορη από την κίνηση της μοριακής περιστροφής. Η επίδραση ενός ηλεκτρομαγνητικού πεδίου (π.χ. φως από laser) πάνω σε ένα μόριο έχει ως αποτέλεσμα την απορρόφηση ενέργειας από αυτό όταν ικανοποιείται η συνθήκη:

(1)

όπου ΔΕ είναι η διαφορά ενέργειας μεταξύ δύο κβαντικών καταστάσεων του μορίου, h η σταθερά του Planck (h=6.6262 x 10^-34 J s) και ν η συχνότητα του προσπίπτοντος φωτός. Αν η ποσότητα ΔΕ ορίζει την διαφορά δύο ενεργειακών επιπέδων, και ενός υψηλότερου κβαντικού επιπέδου ,

, (2)

τότε το μόριο απόρροφά ενέργεια όταν διεγείρεται από το στο , ενώ εκπέμπει ακτινοβολία στην αντίθετη περίπτωση (® ).

Γίνεται αμέσως αντιληπτό από την σχέση (1) ότι το φαινόμενο Raman είναι ένα κβαντικό φαινόμενο και η θεωρία που το περιγράφει πλήρως κάνει ευρύτατη χρήση εννοιών της κβαντικής θεωρίας. Παρ’ όλα αυτά, είναι δυνατόν να καταλήξει κανείς σε μερικά γενικά συμπεράσματα μέσω μιας κλασσικής προσέγγισης του φαινομένου. Οι θεμελιώδεις φυσικές αρχές που διέπουν την κλασσική ερμηνεία του φαινομένου μπορούν να συνοψιστούν ως εξής:

Το προσπίπτον φως πολώνει τα μόρια του μέσου με το οποίο αλληλεπιδρά επάγωντας κατά τον τρόπο αυτό ταλαντούμενα ηλεκτρικά δίπολα. Σύμφωνα με την κλασσική ηλεκτροδυναμική θεωρία επιταχυνόμενα φορτία έχουν την δυνατότητα να ακτινοβολούν. Η δευτερογενής αυτή ακτινοβολία των διπόλων είναι η σκέδαση.

Η σκέδαση της ηλεκτρομαγνητικής ακτινοβολίας προέρχεται από την αλληλεπίδραση των φωτονίων με το ηλεκτρονιακό νέφος. Με άλλα λόγια το φως σκεδάζεται από τα ηλεκτρόνια του μορίου και όχι από τους πυρήνες.

Η σκέδαση Raman αποδίδεται στην σύζευξη των κινήσεων των ηλεκτρονίων και των πυρήνων. Η διαμόρφωση των θέσεων των πυρήνων καθορίζει το ενδομοριακό πεδίο το οποίο “καταλαβαίνουν” τα ηλεκτρόνια. Η παραμορφωσιμότητα του ηλεκτρονιακού νέφους από το προσπίπτον ηλεκτρικό πεδίο εξαρτάται από την στιγμιαία διαμόρφωση των πυρηνικών συντεταγμένων. Έτσι, καθώς οι πυρήνες δονούνται γύρω από τις θέσεις ισορροπίας τους, η παραμορφωσιμότητα των ηλεκτρονιακών νεφών μεταβάλλεται με την συχνότητα δόνησης των πυρήνων. Επιπλέον, η ταλάντωση του ηλεκτρονιακού νέφους με την σειρά της επηρεάζει την δόνηση των πυρήνων του μορίου.

Μπορούμε τώρα να δούμε την τάξη των ενεργειακών διαφορών που προκύπτουν στο σκεδαζόμενο φως. Τα χαμηλότερης ενέργειας περιστροφικά επίπεδα εμφανίζονται στην περιοχή 1–100 cm^-1.^(*
) Το γεγονός ότι τα δονητικά επίπεδα ενός μορίου απέχουν περισσότερο από περιστροφικά συνεπάγεται ότι η μεταβάσεις μεταξύ αυτών θα γίνονται σε μεγαλύτερες συχνότητες, βλ. Σχέση (1). Έτσι, οι τυπικές τιμές συχνοτήτων (ή κυματαριθμών) στις οποίες παρατηρούνται τα δονητικά φάσματα κυμαίνονται στο διάστημα 10²–10⁴ cm^-1. Τέλος, οι ηλεκτρονιακές ενεργειακές στάθμες απέχουν αρκετά περισσότερο μεταξύ τους και καταγράφονται στην περιοχή πάνω από 10⁴ cm^-1.

Σχήμα 1. Σχηματικό διάγραμμα των ενεργειακών επιπέδων ενός μορίου. Οι πραγματικές διαφορές ενέργειας των ηλεκτρονιακών επιπέδων είναι πολύ μεγαλύτερες από αυτές του σχήματος, ενώ οι αντίστοιχες των περιστροφικών είναι αρκετά μικρότερες.

Στο πιο πάνω σχήμα φαίνονται οι πιθανές ενεργειακές μεταβάσεις ενός μορίου. Πρέπει εδώ να τονίσουμε το γεγονός ότι δεν είναι όλες οι μεταβάσεις αυτές πιθανές. Η διακρίβωση αν μια μετάβαση είναι επιτρεπτή ή απαγορευμένη γίνεται μέσω ειδικών σχέσεων που ονομάζονται κανόνες επιλογής, οι οποίοι καθορίζονται από την συμμετρία του μορίου. Τέτοια θέματα παρ’ όλο που δείχνουν αρκετά δύσκολα για πολυατομικά μόρια αντιμετωπίζονται σχετικά εύκολα με έναν μεθοδικό τρόπο με την βοήθεια της θεωρίας ομάδων.

Β. Κλασσική προσέγγιση του φαινομένου Raman

Επανερχόμενοι στο θέμα της κλασσικής ερμηνείας του φαινομένου Raman μπορούμε να προσεγγίσουμε το θέμα ως ακολούθως. Το προσπίπτον φως περιγράφεται από ένα επίπεδο κύμα για το οποίο η ισχύς του ηλεκτρικού-του πεδίου (πλάτος ταλάντωσης) περιγράφεται από την σχέση,

(3)

Το πεδίο αυτό επάγει μια διπολική ροπή σε ένα μόριο ανάλογη του μεγέθους του,

(4)

όπου η ποσότητα είναι η πολωσιμότητα του μορίου, (Σχήμα 2).

Σχήμα 2. Δημιουργία διπολικής ροπής επαγωμένης από την εφαρμογή ηλεκτρικού πεδίου ενός ηλεκτρομαγνητικού κύματος.

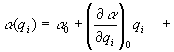Στην κλασσική προσέγγιση του φαινομένου, η πολωσιμότητα είναι μια φαινομενολογική παράμετρος. Ας υποθέσουμε τώρα ότι η πολωσιμότητα εξαρτάται από την απόσταση μεταξύ των πυρήνων για κάθε χρονική στιγμή. Αν q_i είναι μια “δονητική συντεταγμένη” που περιγράφει την δόνηση ενός μορίου, τότε μπορούμε να θεωρήσουμε ότι . Θεωρώντας την ποσότητα q_i αρκετά μικρή μπορούμε να αναπτύξουμε την πολωσιμότητα σε μια σειρά δυνάμεων γύρω από το σημείο ισορροπίας της συντεταγμένης q_i=0:

όροι υψηλότερης τάξης (5)

Η ποσότητα είναι η πολωσιμότητα στην θέση ισορροπίας και είναι ο ρυθμός αλλαγής της πολωσιμότητας σε σχέση με την αλλαγή στην μεταβλητή q_i. Θεωρώντας ότι το μόριο δονείται με συχνότητα ω_i μπορούμε να γράψουμε,

(6)

οι εξισώσεις (3)-(6) δίνουν:

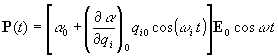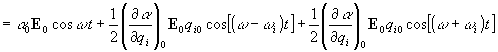= (7)

Η εξίσωση (7) περιέχει τρεις όρους. Ο πρώτος όρος περιγράφει ένα ταλαντούμενο δίπολο το οποίο ακτινοβολεί στην συχνότητα του προσπίτοντος φωτός ω, (σκέδαση Rayleigh). Οι επόμενοι δύο όροι εμπεριέχουν διαφορές στην συχνότητα ακτινοβολίας του διπόλου. Έτσι το σκεδαζόμενο φωτόνιο μπορεί να κερδίσει ενέργεια και να εκπεμφθεί με συχνότητα ω+ω_i (σκέδαση anti-Stokes) ή να εκπεμφθεί χάνοντας ενέργεια, σε συχνότητα ω-ω_i (σκέδαση Stokes). Παρατηρούμε ότι αν η ποσότητα είναι μηδέν τότε επιβιώνει μόνο ο πρώτος όρος της σχέσης (7) δίνοντας αποκλειστικά ελαστική σκέδαση. Άρα, για να έχουμε σκέδαση Raman, απαραίτητη προϋπόθεση είναι η μεταβολή της πολωσιμότητας κατά την διάρκεια της δόνησης.

Τέλος ενδεικτικά αναφέρουμε ότι η σκέδαση είναι ένα αρκετά ασθενές και σπάνιο να συμβεί φαινόμενο. Έτσι, αν Ι_προσπ., Ι_Rayl. και Ι_Raman είναι οι εντάσεις του προσπίπτοντος, του ελαστικά σκεδαζόμενου και του κατά Raman σκεδαζόμενου φωτός, ισχύει προσεγγιστικά η σχέση αναλογίας: Ι_προσπ./ Ι_Rayl. / Ι_Raman µ 1 / 10^-3 / 10^-7, δηλαδή μόνο το ένα στα 10 δις. προσπίπτοντα φωτόνια σκεδάζονται κατά Raman. Η ασθενής φύση του φαινομένου απαιτεί την ύπαρξη πολύ ισχυρών πηγών ακτινοβολίας όπως π.χ. ενός laser.

Η μέχρι τώρα περιγραφή είναι μια πολύ απλοποιημένη εικόνα προσέγγισης του φαινομένου. Για παράδειγμα η παράμετρος αναλογίας μεταξύ P και Ε δηλαδή η πολωσιμότητα, δεν είναι απλός αριθμός αλλά τανυστής. Αυτό σημαίνει ότι το ηλεκτρονιακό νέφος των ατόμων εμφανίζει διαφορετικό βαθμό στην ευκολία ή δυσκολία πόλωσής του στις διάφορες διευθύνσεις. Μπορεί να δειχτεί ότι η σκεδαζόμενη ένταση Raman είναι ανάλογη του τετραγώνου της μεταβολής της πολωσιμότητας και της τετάρτης δύναμης της σκεδαζόμενης συχνότητας του μη-ελαστικά σκεδαζόμενου φωτονίου,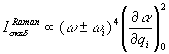

(8)

όπου ω και ω_i είναι οι κυματάριθμοι φωτός και δόνησης αντίστοιχα, ενώ τα πρόσημα αντιστοιχούν σε σκέδαση Stokes (-) και anti–Stokes (+). Επίσης, λόγω του γεγονότος ότι η κατάληψη των δονητικών επιπέδων ακολουθεί κατανομή Boltzmann, ο λόγος των εντάσεων Stokes και anti–Stokes δίνεται από την σχέση,

. (9)

Σχήμα 3. Σχηματική αναπαράσταση του τρόπου της πειραματικής μέτρησης του λόγου αποπόλωσης.

Η διεύθυνση της επαγώμενης από το ηλεκτρικό πεδίο διπολικής ροπής εξαρτάται από την συμμετρία του μορίου. Η κατανομή στον χώρο της ποσότητας για μια δόνηση μπορεί να είναι ισότροπη ή ανισότροπη, εξαρτώμενη από το αν η δόνηση αυτή είναι πλήρως συμμετρική ή αντισυμμετρική.^(**) Πειραματικά έχει κανείς την δυνατότητα να χρησιμοποιήσει δύο διαφορετικές γεωμετρίες σκέδασης σχετικά με το επίπεδο σκέδασης. Το τελευταίο ορίζεται ώς το επίπεδο που ορίζουν οι διευθύνσεις πρόσπτωσης και παρατήρησης της ακτινοβολίας, επίπεδο xy στο Σχήμα 3.

Ο λόγος αποπόλωσης ορίζεται ως ο λόγος της σκεδαζόμενης έντασης που είναι κάθετη στο επίπεδο σκέδασης (Ι_z) ως προς την ένταση που είναι παράλληλη με το επίπεδο σκέδασης (Ι_y),

. (10)

Η ποσότητα αυτή σχετίζεται άμεσα με τα στοιχεία του τανυστή της πολωσιμότητας και μπορεί να δώσει πληροφορίες σχετικά με την συμμετρία κάποιου τρόπου δόνησης. Έτσι στην περίπτωση που το προσπίπτον φως είναι πολωμένο ο λόγος αυτός κυμαίνεται στα όρια 0 £ ρ £ 3/4. Όταν για κάποια δόνηση ισχύει 0 £ ρ < 3/4, τότε η μετρούμενη κορυφή στο φάσμα που οφείλεται στην δόνηση αυτή λέγεται πολωμένη ενώ όταν ρ=3/4 αποπολωμένη.

Γ. Κανονικές συντεταγμένες και κανονικοί τρόποι δόνησης

Στην περίπτωση ενός διατομικού μορίου είναι πολύ εύκολο να αντιληφθούμε τον τρόπο δόνησης αφού η κίνηση των ατόμων είναι πάνω στην ευθεία που ενώνει τους πυρήνες τους. Το θέμα αυτό όμως γίνεται αρκετά περίπλοκο όταν ο αριθμός των ατόμων αυξάνει. Μπορεί να δειχθεί ότι η περίπλοκη δόνηση των πολυατομικών μορίων είναι δυνατόν να παρασταθεί ως μια υπέρθεση συνιστωσών που ονομάζονται κανονικοί τρόποι δόνησης. Μετά από συγκεκριμένους μετασχηματισμούς των συντεταγμένων θέσης και ορμής μπορεί κανείς να περιγράψει την κινητική και δυναμική ενέργεια ενός πολυατομικού μορίου κατά τρόπο ώστε η κάθε νέα μεταβλητή (κανονική συντεταγμένη) να εμφανίζεται στις εξισώσεις κίνησης μόνο ως γινόμενο με τον εαυτό της. Αυτή η διαδικασία απλοποιεί αρκετά την ανάλυση δίνοντας ταυτόχρονα και ιδιαίτερη φυσική σημασία στις κανονικές δονήσεις. Η φυσική αυτή σημασία αντανακλά στο γεγονός ότι σε μια κανονική δόνηση όλοι οι πυρήνες του μορίου κινούνται σε φάση και με την ίδια συχνότητα.

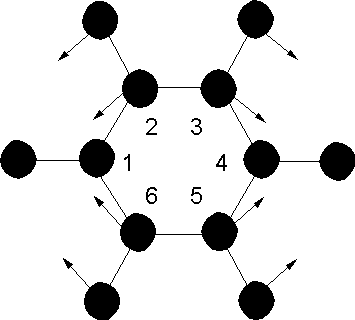
Στην γενική περίπτωση ενός μορίου με Ν άτομα είναι προφανές ότι ο αριθμός των κανονικών τρόπων δόνησης είναι 3Ν–6, αφού έξι τρόποι κίνησης απαιτούνται για την περιγραφή της περιστροφικής (3) και της μεταφορικής (3) κίνησης του μορίου. Τα γραμμικά μόρια έχουν 3Ν–5 τρόπους δόνησης αφού εδώ δεν υπάρχει περιστροφικός βαθμός ελευθερίας γύρω από τον μοριακό άξονα.

Ας εξετάσουμε την απλή περίπτωση ενός γραμμικού τριατομικού μορίου, π.χ. CO₂. Όπως αναφέραμε αναμένονται 3x3–5=4 κανονικοί τρόποι δόνησης οι οποίοι φαίνονται στο Σχήμα 4α. Σε κάθε τρόπο δόνησης τα άτομα διενεργούν μια απλή αρμονική κίνηση κατά την διεύθυνση που ορίζει το βέλος έχοντας όλα την ίδια συχνότητα. Μια σημαντική παρατήρηση προκύπτει για τις δονήσεις ν₂, οι οποίες έχουν μεταξύ τους την ίδια συχνότητα. Υπό την έννοια αυτή οι δονήσεις αυτές λέγονται διπλά εκφυλισμένες δονήσεις. Στην περίπτωση του μορίου του νερού έχουμε στο Σχήμα 4β τους 3x3–6=3 κανονικούς τρόπους δόνησης όπως αναμένεται.

Σχήμα 4. Κανονικοί τρόποι δόνησης των μορίων CO₂ και Η₂Ο. (Τα σύμβολα + και – αντιστοιχούν σε δονήσεις με διευθύνσεις κάθετες στο επίπεδο του χαρτιού, προς τα πάνω και κάτω αντίστοιχα.

Μπορούμε τώρα να εστιαστούμε στο θέμα της δυνατότητας να είναι μια δόνηση ενεργή κατά Raman. Ας θυμηθούμε ότι η κύρια προϋπόθεση για να συμβαίνει αυτό είναι να έχουμε μεταβολή της πολωσιμότητας κατά την δόνηση. Εξετάζοντας τα δύο συγκεκριμένα παραδείγματα κανονικών τρόπων δόνησης που μόλις είδαμε, έχουμε τα εξής:

Μόριο
Κανονικός τρόπος Δόνησης
Μεταβολή της πολωσιμότητας
Παράγωγος της πολωσιμότητας	¹ 0	= 0	= 0
Ενεργότητα κατά Raman	NAI	OXI	OXI

Μόριο
Κανονικός τρόπος Δόνησης
Μεταβολή της πολωσιμότητας
Παράγωγος της πολωσιμότητας	¹ 0	¹ 0	¹ 0
Ενεργότητα κατά Raman	NAI	NAI	ΝΑΙ

Από τα παραπάνω παραδείγματα διαφαίνεται ο σημαντικός ρόλος της συμμετρίας του μορίου και των τρόπων δόνησής τους στον προσδιορισμό της ενεργότητας κατά Raman.

Τέλος, σαν χαρακτηριστικό παράδειγμα αναπαριστούμε στο Σχήμα 5 το φάσμα Raman του μορίου του τετραχλωράνθρακα ενώ στο Σχήμα 6 δείχνονται οι τέσσερις κανονικοί τρόποι δόνησης ενός τετραεδρικού μορίου.

Σχήμα 5. Φάσμα Raman του μορίου του CCl₄. Η κορυφή ν₃ της περιοχής anti-Stokes έχει μεγεθυνθεί κατά 100 φορές. Τα σκεδαζόμενα φωτόνια μέσω μηχανισμού Stokes έχουν μικρότερες συχνότητες από την συχνότητα της προσπίπτουσας (§ 1Β) γι’ αυτό και παρουσιάζονται εδώ με αρνητικό πρόσημο. Επειδή όμως η σκέδαση Raman Stokes είναι ισχυρότερη (λόγω κατανομής Boltzmann) από την σκέδαση Raman anti-Stokes τα φάσματα Raman μετρώνται κατά κανόνα στην περιοχή Stokes όπου κατά σύμβαση θα παρουσιάζονται χωρίς πρόσημο.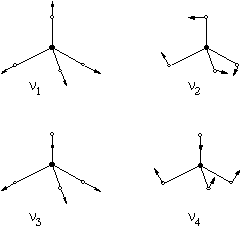

Σχήμα 6. Κανονικοί τρόποι δόνησης ενός τετραεδρικού μορίου.

2. Πειραματικό Μέρος

Η παρούσα άσκηση έχει ως σκοπό την εισαγωγή και την εξοικείωση των φοιτητών με την οργανολογία της φασματοσκοπίας Raman και με την μελέτη μέσω αυτής απλών οργανικών υγρών.

Α. Οργανολογία Raman

Μια τυπική φασματοσκοπική τεχνική Raman (βλ. Σχ. 5) αποτελείται από τις εξής συνιστώσες:

Μονοχρωματική πηγή ακτινοβολίας (συνήθως LASER συνεχούς ακτινοβολίας).

Σύστημα κατεύθυνσης, προσανατολισμού και πόλωσης της ακτινοβολίας.

Υποδοχή τοποθέτησης του υπό μελέτη δείγματος (οπτικός φούρνος ή κρυοστάτης).

Ένας διπλός ή τριπλός μονοχρωμάτορας για την ανάλυση του σκεδαζόμενου φωτός.

Ηλεκτρονικό σύστημα ανίχνευσης, ενίσχυσης και καταγραφής του σήματος.

Καθρέπτης

Φακοί

Η/Υ Μονοχρωμάτορας

Laser

Σχήμα 7. Απλουστευμένο διάγραμμα μιας τυπικής φασματοσκοπίας Raman.

Μπορούμε τώρα να περιγράψουμε συνοπτικά τα προαναφερθέντα βασικά στοιχεία της φασματοσκοπίας Raman.

Απαραίτητη προϋπόθεση για την καταγραφή των κορυφών που οφείλονται στα δονητικά επίπεδα του υλικού είναι η παρουσία μιας αρκετά ισχυρής και μονοχρωματικής ακτινοβολίας, τέτοια δυνατότητα παρέχεται από τα LASERs. Τα πλέον διαδεδομένα LASERs αερίου (Ar⁺ και Kr⁺) χρησιμοποιούνται ευρέως για φασματοσκοπικούς σκοπούς. Οι ισχυρότερες ακτινοβολίες (ή γραμμές) είναι π.χ. για το LASER του Ar⁺ στα 488.0 και 514.5 nm, στο μπλε και πράσινο αντίστοιχα.

Το σύστημα κατεύθυνσης, προσανατολισμού και πόλωσης της ακτινοβολίας αποτελείται από τα εξής οπτικά στοιχεία: (i) Καθρέπτες υψηλής ανακλαστικότητας. (ii) Φακοί για την εστίαση της δέσμης του LASER. Για παράδειγμα δέσμη φωτός μήκους κύματος 500 nm με διάμετρο 1.5 cm αν εστιαστεί με φακό εστιακής απόστασης 10 cm αποκτά διάμετρο περίπου 4x10^-3 cm. Αυτή η κατά 1000 φορές περίπου μείωση της ενεργού διατομής της δέσμης επιφέρει αντίστοιχη αύξηση της ακτινοβόλησης ανά μονάδα επιφάνειας. (iii) Πολωτές και αναλυτές για την επιλογή της κατάλληλης γεωμετρίας πόλωσης, (βλ. Παρ. 1.Β). Τέλος χρησιμοποιούνται αρκετά συχνά ειδικά φίλτρα για την απαλλαγή ανεπιθύμητων συνιστωσών ακτινοβολίας κυρίως στα LASERs αερίου.

Η ανάγκη για την μελέτη των υλικών στις διάφορες φάσεις τους (στερεά, υγρή, αέρια) έχει ωθήσει στην δημιουργία συσκευών ελέγχου θερμοκρασίας. Έτσι, οπτικοί φούρνοι χρησιμοποιούνται όταν θέλει κανείς να καταγράψει τα φάσματα Raman σε θερμοκρασίες αρκετά υψηλότερες από αυτήν του περιβάλλοντος (τήγματα, αέρια) και κρυοστάτες για την επίτευξη πολύ χαμηλών θερμοκρασιών, (για ενώσεις που είναι υγρά στην θερμοκρασία περιβάλλοντος και για άμορφα υλικά όταν ενδιαφέρουν οι ιδιότητες των πολύ χαμηλών θερμοκρασιών).

Ο μονοχρωμάτορας αποτελεί το μέσο ανάλυσης ή διασποράς της σκεδαζόμενης ακτινοβολίας. Αποτελείται από καθρέπτες και φράγματα περίθλασης τα οποία είναι και τα οπτικά στοιχεία που διαχωρίζουν το σκεδαζόμενο φως σε μικρές παράλληλες δέσμες διαφορετικής ενέργειας. Τα φράγματα περίθλασης έχουν την μορφή επίπεδων καθρεπτών πάνω στους οποίους έχουν χαραχθεί με πολύ μεγάλη ακρίβεια αύλακες, των οποίων οι αποστάσεις καθορίζουν την εικόνα περίθλασης, ενώ τυπικές τιμές είναι περίπου 1800 αύλακες/mm. Μεταξύ των φραγμάτων περίθλασης και των καθρεπτών του μονοχρωμάτωρα παρεμβάλλονται σχισμές το μέγεθος των οποίων είναι μεταβλητό καθορίζοντας έτσι την αναλυτική (διακριτική) ικανότητα του οργάνου.

Το αναλυμένο σήμα όταν εξέλθει από τον μονοχρωμάτορα είναι αρκετά ασθενές, για τον σκοπό αυτό η πρόσπτωσή του πάνω στην ευαίσθητη επιφάνεια ενός ανιχνευτή συνοδεύεται από ηλεκτρονική ενίσχυση. Στην θέση του ανιχνευτή μπορεί να υπάρχει φωτοπολλαπλασιαστής στην περίπτωση που η καταγραφή γίνεται με σάρωση (στροφή των φραγμάτων περίθλασης γύρω από τον άξονά τους έτσι ώστε να φτάνει κάθε χρονική στιγμή συγκεκριμένη δέσμης ενέργειας στον ανιχνευτή) ή σε άλλες περιπτώσεις με στοιχείο συζευγμένου φορτίου (CCD) για στιγμιαία καταγραφή προκαθορισμένου ενεργειακού “παραθύρου” του φάσματος. Τέλος, η χρήση κατάλληλου λογισμικού στον υπολογιστή είναι απαραίτητη για την συλλογή και επεξεργασία του φάσματος.

Β. Μετρήσεις

Σκοπός της συγκεκριμένης άσκησης είναι η εξοικείωση των εκπαιδευομένων με τις βασικές αρχές της φασματοσκοπίας Raman. Έτσι, το κύριο στάδιο της διαδικασίας είναι η καταγραφή των φασμάτων Raman για απλά οργανικά υγρά, π.χ. τετραχλωράνθρακα και βενζόλιο, σε διάφορες πολώσεις και στις περιοχές τόσο των ενεργειών Stokes όσο και των anti–Stokes.

Στάδιο 1:

Καταγράψτε τα φάσματα Stokes και anti–Stokes για τον τετραχλωράνθρακα και το βενζόλιο, σε γεωμετρίες πόλωσης VV και HV. Παρατηρήστε τις αλλαγές στις εντάσεις των κορυφών τόσο μεταξύ του Stokes και anti–Stokes της ίδιας πόλωσης όσο και μεταξύ του πολωμένου και αποπολωμένου φάσματος της ίδιας ενεργειακής περιοχής.

Συγκρίνετε τις κορυφές δόνησης που παρατηρείτε με τον θεωρητικά αναμενόμενο αριθμό των κανονικών τρόπων δόνησης που αναμένεται για κάθε ένωση.

Υπολογίστε τους λόγους αποπόλωσης για τις κορυφές του τετραχλωράνθρακα που βρίσκονται στους 215, 314 και 459 cm^-1 και συγκρίνετέ τους με τους αντίστοιχους θεωρητικά αναμενόμενους.

Αφού συγκρίνετε τις εντάσεις Stokes και anti–Stokes, υπολογίστε την θερμοκρασία στην οποία καταγράφηκαν τα φάσματα δόνησης των ενώσεων που μελετάτε.

Στάδιο 2:

Αυξήστε την αναλυτική ικανότητα του μονοχρωμάτορα (μειώνοντας τις διαστάσεις των κατάληλων σχισμών) και εστιάστε την καταγραφή του φάσματος στην περιοχή της κύριας κορυφής δόνησης του τετραχλωράνθρακα, στους 459 cm^-1. Θα παρατηρήσετε ότι η φαινομενικά μία (ασύμμετρη) κορυφή διαχωρίζεται τώρα πλέον σε περισσότερες οξείες κορυφές. Το φαινόμενο αυτό οφείλεται στην ύπαρξη δύο διαφορετικών ισοτόπων του ατόμου του Cl. Τα ισότοπα με ατομικό βάρος 35 και 37 υπάρχουν στην φύση σε αναλογία περίπου 75% και 25% αντίστοιχα. Η ύπαρξη των δύο ισοτόπων συνεπάγεται ότι το τεράεδρο CCl₄ μπορεί να βρεθεί στις πέντε διαμορφώσεις που φαίνονται στο πιο κάτω σχήμα. Η πιθανότητα ύπαρξης του κάθε τετραέδρου είναι συνάρτηση του ποσοστού ύπαρξης του κάθε φυσικού ισοτόπου, και η δόνηση του κάθε τετραέδρου από τα (α)–(ε) είναι υπεύθυνη για την ύπαρξη των επιμέρους κορυφών της δόνησης στους 459 cm^-1.

ΑΣΚΗΣΗ 2

ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΗΣ ΚΡΥΣΤΑΛΛΙΚΟΤΗΤΑΣ ΠΟΛΥΜΕΡΩΝ ΜΕ ΦΑΣΜΑΤΟΣΚΟΠΙΑ RAMAN

Σκοπός της άσκησης είναι ο προσδιορισμός της διεπιφανειακής στοιβάδας μεταξύ της κρυσταλλικής και της άμορφης φάσης σε ημικρυσταλλικά πολυμερή με την χρησιμοποίηση δονητικής φασματοσκοπίας Raman. Εφαρμογή στο πολυαιθυλένιο.

Θεωρητικό μέρος
Τα μακρομόρια είναι δυνατό να υπάρξουν στην κατάσταση αταξίας ή άμορφη φάση και στην κατάσταση τάξης ή κρυσταλλική φάση (Εικόνα 1).

Στην άμορφη φάση οι επιμέρους αλυσίδες ακολουθούν στατιστική διαμόρφωση που καλείται και τυχαία περιέλιξη (random coil). Τα κέντρα μάζας των μακρομορίων είναι επίσης τυχαία κατανεμημένα το ένα έναντι του άλλου. Όλες οι δομικές και θερμοδυναμικές ιδιότητες που παρατηρούνται σ’ αυτή τη φάση είναι δυνατό να συσχετιστούν μ’ αυτές ενός υγρού με πολύ υψηλό ιξώδες.

Εικόνα 1. Σχηματική απεικόνιση διαμορφώσεων μακρομοριακών αλυσίδων στην άμορφη

και κρυσταλλική φάση (Από αναφορά [1]).

Η κρυσταλλική φάση χαρακτηρίζεται από τριών διαστάσεων διευθέτηση σ’ ένα τμήμα τουλάχιστον των αλυσίδων. Η υπό διάταξη διαμόρφωση είναι δυνατό να επεκταθεί ή να αναπαρασταθεί με μια ελικοειδή δομή.

Την τελευταία εικοσαετία έχει υπάρξει αυξημένη ερευνητική δραστηριότητα για την διερεύνηση ύπαρξης μιας τρίτης (ή και τέταρτης φάσης) σε ημικρυσταλλικά πολυμερή. Η νέα αυτή φάση αναφέρεται ως ένα στρώμα μεταξύ του κρυσταλλικού και του άμορφου πολυμερικού υλικού. Πρόκειται για μια ανισοτροπική άμορφη φάση όπου τμήματα των αλυσίδων έχουν απολέσει την εγκάρσια τάξη αλλά έχουν διατηρήσει μια εκτεταμένη διαμόρφωση.

Η εισαγωγή μιας τρίτης φάσης με διαφορετικές μηχανικές ιδιότητες φαίνεται να δίνει τη δυνατότητα επιτυχούς προσομοίωσης πειραματικών μηχανικών δεδομένων εκεί όπου μοντέλα δύο φάσεων αποτυγχάνουν. Με τη φασματοσκοπία είναι δυνατό να προσδιοριστεί το κλάσμα της τρίτης αυτής διαχωριστικής φάσης στο πολυμερικό υλικό και με τη χρησιμοποίηση μοντέλων τριών φάσεων να γίνει εφικτή μια πληρέστερη περιγραφή των μηχανικών ιδιοτήτων ημικρυσταλλικών ομοπολυμερών. Οι πειραματικές τεχνικές που έχουν χρησιμοποιηθεί για την επιβεβαίωση ύπαρξης της νέας αυτής φάσης είναι μεταξύ άλλων το NMR H⁺ & C¹³, μετρήσεις ειδικής θερμότητας και διηλεκτρικής επαναφοράς, η σκέδαση νετρονίων και ακτινών Χ μικρών γωνιών, η σκέδαση Raman. Ανάλογα συμπεράσματα έχουν διαμορφωθεί από την ανάλυση μοριακών προσομοιώσεων.

Στην παρούσα άσκηση θα χρησιμοποιηθεί η φασματοσκοπία Raman για τον προσδιορισμό της ενδιάμεσης φάσης, καθώς και των αντίστοιχων της άμορφης και της κρυσταλλικής, ενός ημικρυσταλλικού πολυμερούς όπως το πολυαιθυλένιο.

Πειραματικό μέρος
Για τον προσδιορισμό της διεπιφανειακής στοιβάδας μεταξύ της κρυσταλλικής και της άμορφης φάσης ημικρυσταλλικών πολυμερών η άσκηση θα εστιαστεί στη μελέτη δοκιμίων πολυαιθυλενίου με διαφορετική κρυσταλλικότητα. Τα μοριακά χαρακτηριστικά των πολυμερών που θα χρησιμοποιηθούν καθώς και το υψηλής τάξης n-αλκάνιο που υποκαθιστά το κρυσταλλικό πολυαιθυλένιο αναγράφονται στον Πίνακα 1. Τα δείγματα είναι υπό διάφορες μορφές, όπως φιλμ, σκόνη, σφαιρίδια. Για την χρησιμοποίηση της φασματοσκοπίας Raman επισημαίνεται ότι δεν χρειάζεται προετοιμασία δείγματος. Επιπλέον, με τη χρησιμοποίηση των οργανολογιών micro-Raman ή FT-Raman η ποσότητα του δείγματος που απαιτείται είναι ελάχιστη. Για παράδειγμα, στο micro-Raman η χωροδιακριτότητα (spatial resolution) του μικροσκοπίου όπως και η εστίαση της δέσμης του laser (λο=514.5 nm) στο δείγμα με τον x100 αντικειμενικό φακό είναι της τάξης του 1μm.

Πίνακας Ι. Μοριακά χαρακτηριστικά των χρησιμοποιουμένων πολυμερών

Α/Α	Πολυμερές	Mw	ρ (g/cm³)	σημείο τήξεως (^οC)	Προέλευση
1.	LLDPE (Linear Low Density PE)	100,000	0,87	57	Dow
2.	LLDPE (Linear Low Density PE)	80,000	0,90	104	Dow
3.	LLDPE (Linear Low Density PE)	120,000	0,92	126	Dow
4.	LDPE (Linear Density PE)		0,922		Aldrich
5.	MDPE (Medium Density PE)		0,940	109-111	Aldrich
6.	UHMWPE (Ultra High Molecular Weight PE)	3,000,000 έως 6,000,000	0,940	138	Aldrich
7.	HDPE (High Density PE)		0,962	125-140	Aldrich
8.	CH₃(CH₂)₅₈CH₃ (Hexacontane)			96-100	Aldrich

Το γραμμικό χαμηλής πυκνότητας πολυαιθυλένιο (LLDPE) κατ’ ουσία είναι ένα συμπολυμερές αιθυλενίου με 5-10% είδη αλκενίων (βουτένιο-1 [CH₃CH₂CH=CH₂] ή εξένιο-1 [CH₃CH₂CH₂CH₂CH=CH₂] ή οκτένιο-1 [CH₃CH₂CH₂CH₂CH₂CH₂CH=CH₂) που συνιστούν διακλαδώσεις της κύριας αλυσίδας του πολυαιθυλενίου. Για παράδειγμα το δοκίμιο (1) περιέχει ~10% οκτένιο-1, το δοκίμιο (2) 5% οκτένιο-1, ενώ το δοκίμιο (3) περιέχει μόνο μικρές διακλαδώσεις προερχόμενες από βουτένιο ή/και εξένιο. Η ύπαρξη μεγαλυτέρων διακλαδώσεων μειώνει την πυκνότητα των αντίστοιχων πολυμερών. Οι διακλαδώσεις των οκτενίων ως πιο επιμήκεις εμποδίζουν την επισώρευση των μακροαλυσίδων περισσότερο απ’ ότι οι διακλαδώσεις των βουτενίων και παρουσιάζουν μειωμένη κρυσταλλικότητα.

Το φάσμα Raman του πολυαιθυλενίου

Το συνολικό φάσμα Raman ενός τυπικού δοκιμίου πολυαιθυλενίου φαίνεται στο Σχήμα 1. Πρόκειται για την Stokes περιοχή του φάσματος Raman που έχει ληφθεί με οργανολογία FT-Raman.

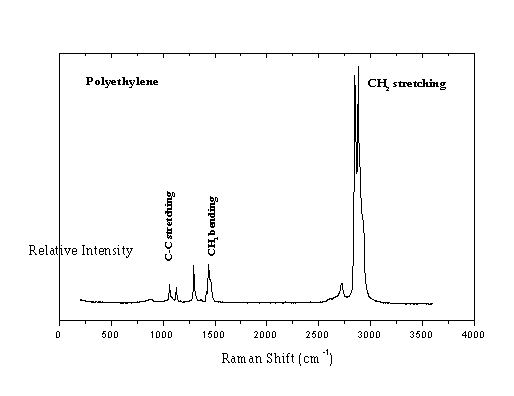
Σχήμα 1. Το φάσμα Raman ενός τυπικού δοκιμίου πολυαιθυλενίου

Τα κύρια χαρακτηριστικά του φάσματος δόνησης του πολυαιθυλενίου συνοψίζονται:

(α) Στη ζώνη σκέδασης στις υψηλές συχνότητες γύρω στους 2900 cm^-1 (λεπτομέρειες στο Σχήμα 2) που αποδίδεται κυρίως στις συμμετρικές και αντισυμμετρικές δονήσεις τάσης Σχήμα 2. Το φάσμα Raman στις υψηλές συχνότητες τριών δοκιμίων πολυαιθυλενίου (δοκίμια 1, 2 & 3) που παρουσιάζουν διαφορετική κρυσταλλικότητα.

του μεθυλενίου CH₂ και στις τρεις φάσεις. Στην ίδια περιοχή συχνοτήτων, υπάρχει αξιοσημείωτη αλλά σε μικρότερο βαθμό συνεισφορά στην σκεδαζόμενη ακτινοβολία Raman από αντίστοιχες δονήσεις του μεθυλίου, CH₃, προερχόμενες από απολήξεις μακροαλυσίδων και διακλαδώσεών τους καθώς από δονήσεις τάσης του CH από τριτοταγή άτομα άνθρακα στα σημεία διακλάδωσης.

(β) Στη ζώνη σκέδασης που εμφανίζεται στην περιοχή συχνοτήτων 1000-1500 cm^-1 (Σχήμα 3) και αποδίδεται κυρίως στις σκελετικές δονήσεις τάσης C-C (περιοχή Ι), στις δονήσεις CH₂ στρέψης (περιοχή ΙΙ) και στις δονήσεις CH₂ κάμψης (περιοχή ΙΙΙ).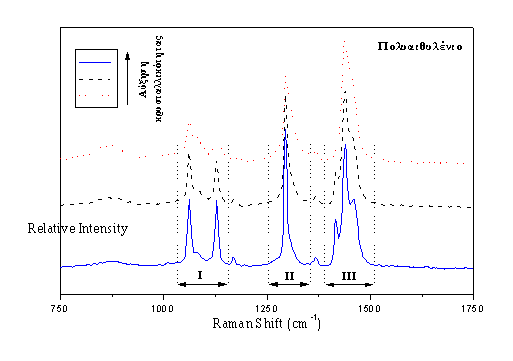

Σχήμα 3. Το φάσμα Raman στις περιοχή συχνοτήτων 1000-1500 cm^-1 τριών δοκιμίων πολυαιθυλενίου (δοκίμια 1, 2 & 3) που παρουσιάζουν διαφορετική κρυσταλλικότητα

Μέθοδος προσδιορισμού κρυσταλλικότητας πολυαιθυλενίου (PE) με την βοήθεια της φασματοσκοπίας Raman.

Στην παρούσα άσκηση θα ακολουθηθεί μια μέθοδος που έχουν προτείνει οι Strobl και Hangedorn [2] για τον υπολογισμό του σχετικού ποσοστού της ορθορομβικής κρυσταλλικής φάσης του PE, α_c, της υγρής (άμορφης) φάσης, α_a, και της ενδιάμεσης, α_b.

Προφανώς α_b+α_c+α_a = 1, όπου τα α_a και α_c μπορούν εύκολα να υπολογιστούν πειραματικά. Οπότε α_b=1-α_c-α_a.

Επί μέρους φασματικές περιοχές

Στο φάσμα Raman ενός ημικρυσταλλικού PE μπορούμε να διακρίνουμε τις εξής χαρακτηριστικές φασματικές περιοχές (Σχήμα 3 & 4).

( Ι ) 1040 - 1160 cm^-1 ð σκελετικές δονήσεις τάσης (stretching) C-C

a) Δύο στενές κορυφές προερχόμενες από την κρυσταλλική φάση στους 1129 και 1062 cm^-1.

b) Στους 1080 cm^-1 εμφανίζεται μια ευρεία κορυφή προερχόμενη από την άμορφη φάση.

( ΙΙ) 1250 - 1350 cm^-1 ð δονήσεις CH₂στρέψης ή συστροφής (twisting)

a) Μια στενή κορυφή στους 1295 cm^-1 από την κρυσταλλική φάση

b) Μια ευρεία κορυφή στους 1303 cm^-1 από την άμορφη φάση

(III) 1390 - 1510 cm^-1 ð δονήσεις CH₂ κάμψης (bending)

a) Μια στενή κορυφή στους 1416 cm^-1, η οποία, όντας απομονωμένη από άλλες συνεισφορές, θα χρησιμοποιηθεί για τον προσδιορισμό της κρυσταλλικής (ορθορομβικής) φάσης που αντιπροσωπεύει

b) Δύο κορυφές με συνεισφορά της άμορφης και της κρυσταλλικής φάσης στους 1440 cm^-1 και στους 1460 cm^-1.

Σχήμα 4. Φάσματα Raman στη φασματική περιοχή της δόνησης C-C (Ι) της CH₂ στρέψης (ΙΙ) και της CH₂ κάμψης (ΙΙΙ) για δείγμα (a) κρυσταλλικό PE στους 25^oC, (b) PE σε τήγμα 150^oC και (c) ημικρυσταλλικό στους 25^oC.(Από αναφορά [2]).
Επιλογή μιας εσωτερικής κορυφής αναφοράς

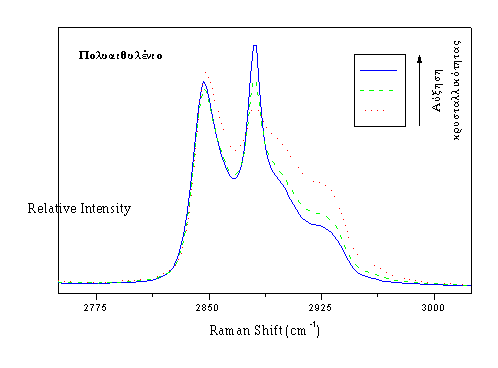
Πειράματα θερμοκρασιακής εξάρτησης των φασμάτων του PE, όπως αυτό που φαίνεται στο Σχήμα 5 για το δοκίμιο (3), έδειξαν ότι στην περιοχή της δόνησης στρέψης (ΙΙ) αλλάζει το περίγραμμα των κορυφών ενώ το εμβαδόν τους παραμένει αμετάβλητο. Αυτό δείχνει ότι το η συνολική σκεδαζόμενη ακτινοβολία Raman, που οφείλεται στην CH₂ δόνηση στρέψης, είναι ανεξάρτητη της διαμόρφωσης των μακρομοριακών αλυσίδων.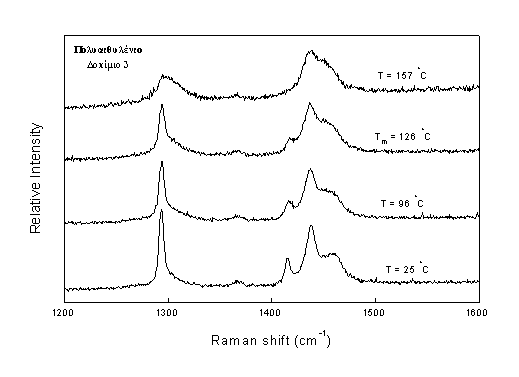

Σχήμα 5. Τα φάσματα Raman ενός ημικρυσταλλικού δοκιμίου PE (δοκίμιο 3) σε διάφορες θερμοκρασίες, απ’ αυτή του περιβάλλοντος έως και πάνω από τη θερμοκρασία τήξης, στις περιοχές δόνησης στρέψης και κάμψης των μεθυλενίων.

Για την επιβεβαίωση αυτού του γεγονότος εξετάστηκε το φάσμα Raman του συμπολυμερούς EVA (αιθυλενίου & βινυλικού αιθυλεστέρα) {[-CH₂-CH₂]_n-[-CH₂-CH(OCOCH₃)-]_n} στην στερεά φάση και στο τήγμα (Σχήμα 6).

Σ’ αυτό το συμπολυμερές ενυπάρχει ένα εγγενές πρότυπο, η ένταση της δόνησης τάσης της απομονωμένης καρβονυλικής ομάδας (C=O) στους ~1740 cm^-1 η οποία και λόγω του εντοπισμένου χαρακτήρα-της παρουσιάζει ισχύ σκέδασης Raman ανεξάρτητη από τη διαμόρφωση της αλυσίδας. Επιπλέον, στα ημικρυσταλλικά δοκίμια του EVA οι μονάδες του βινυλικού αιθυλεστέρα πλασάρονται κατά προτίμηση στις άμορφες περιοχές, οι οποίες δεν επηρεάζονται από διαδικασίες όπως αυτή της τήξης.

Στο Σχήμα 6 λοιπόν παρατηρούμε την περιοχή δόνησης του καρβονυλίου και την περιοχή στρέψης του μεθυλενίου στην “ημικρυσταλλική” φάση (στους 25^οC) και στην άμορφη (στο τήγμα).

Σχήμα 6. Τα φάσματα Raman στην περιοχή CH₂ στρέψης και C=O τάσης ενός συμπολυμερούς EVA (με 16% μονάδες βινυλικού αιθυλεστέρα) στους 25^οC (στερεό) και 95^οC (τήγμα).([2])

Συγκρίνοντας την ολοκληρωμένη σκεδαζόμενη ένταση Raman και των δύο περιοχών φαίνεται πράγματι ότι και η ακτινοβολία Raman που προέρχεται από την δόνηση στρέψης του CH₂ είναι ανεξάρτητη από κάθε διαμόρφωση.

Μπορούμε λοιπόν να τη χρησιμοποιήσουμε ως εσωτερική αναφορά για να συγκρίνουμε τις υπόλοιπες κορυφές στο πολυαιθυλένιο.

Ανάλυση Αποτελεσμάτων

Για να μπορέσουμε να μελετήσουμε τη φασματική συμπεριφορά της άμορφης και κρυσταλλικής φάσης επιλέχτηκαν δυο πρότυπα δείγματα το n-αλκάνιο, C₆₀H₁₂₂ (το οποίο θεωρήθηκε ως πλήρως κρυσταλλικό) , και το PE σε τήγμα (που είναι πλήρως άμορφο).

Τα αποτελέσματα μετρήσεων των εμβαδών των κορυφών των δυο παραπάνω δειγμάτων φαίνονται στον Πίνακα ΙΙ.

Πίνακας ΙΙ. Σχετικές εντάσεις χαρακτηριστικών κορυφών πολυαιθυλενίου από πρότυπα δείγματα.

Εμβαδόν κορυφών Raman
Φασματική Περιοχή	n-αλκάνιο (α_c = 1)	Τήγμα PE (α_a = 1)
(I) I_S = I_{(1120à 1160)} I₁₀₆₂ I₁₁₂₉	1.66 0.77 0.89	0.79
(II) I_T = I_{(1250à 1350)}	1	1
(III) I_B = I_{(1390à 1510)} I₁₄₁₆	2.25 0.46	1.56

Τα εμβαδά υπολογίζονται με προσαρμογή (fitting) Lorentzian κορυφών στην αντίστοιχη φασματική περιοχή που ενδιαφέρει αφού πρώτα κάνουμε διόρθωση γραμμής βάσης (baseline correction). Η διόρθωση αυτή επιτυγχάνεται με αφαίρεση από το φάσμα μιας γραμμής που ενώνει τα ακραία σημεία της φασματικής περιοχής, τα εμβαδά των κορυφών της οποίας θέλουμε να υπολογίσουμε.

Η προσαρμογή των Lorentzian για την εύρεση των εμβαδών γίνεται μέσω κατάλληλου Software (π.χ. Origin) και ανάλογα με την φασματική περιοχή χρησιμοποιείται προσαρμογή με δυο ή τρεις Lorentzian.

I_T = I₁₂₉₅ + I₁₃₀₃

I_S = I₁₀₆₂ + I₁₀₈₀ + I₁₁₂₉

I_B = I₁₄₁₆ + I₁₄₄₀ + I₁₄₆₀

Χρησιμοποιώντας δεδομένα του Πίνακα ΙΙ για το άμορφο τήγμα και το εντελώς κρυσταλλικό δείγμα μπορούμε πολύ εύκολα να υπολογίσουμε το ποσοστό της άμορφης, κρυσταλλικής και ενδιάμεσης φάσης ενός αγνώστου δείγματος πολυαιθυλενίου με τη λήψη ενός φάσματος Raman.

Χρησιμοποιούμε τις εξής εξισώσεις :

α_a = =

α_c = =

α_b = 1 - α_a- α_c

Μπορεί έτσι να συμπληρωθεί ο παρακάτω Πίνακας ΙΙΙ.

Πίνακας ΙΙΙ. Πίνακας πειραματικών αποτελεσμάτων.

	I_T= I₁₂₉₅+ I₁₃₀₃	I₁₀₈₀	α_a=	I	α_c =	α_b = 1 - α_a- α_c
PE

ΑΝΑΦΟΡΕΣ

[1] L. Mandelkern, “The crystalline state”, in Physical Properties of Polymers, Edited by J. Mark, A…[et al.]-2^nd ed., ACS, Washington, DC (1993), p.145.

[2] G.R. Strobl και W.Hagedorn, J. Polym. Science : Polym. Phy., 16, 1181, (1978).

Σημείωση: Η αναπαράσταση όλων των CH₂ τρόπων δόνησης δίδονται στη διεύθυνση http://www.shu.ac.uk/schools/sci/chem/tutorials/molspec/irspec1.htm

ΑΣΚΗΣΗ 3

ΜΕΛΕΤΗ ΤΟΥ ΜΟΡΙΑΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΦΕΛΚΥΣΜΕΝΩΝ ΠΟΛΥΜΕΡΩΝ ΜΕ ΠΟΛΩΜΕΝΑ ΦΑΣΜΑΤΑ RAMAN

Σκοπός της άσκησης είναι η εξοικείωση των φοιτητών στη χρησιμοποίηση πολωμένων φασμάτων Raman για την εκτίμηση του μοριακού προσανατολισμού μονοαξονικά εφελκυσμένων πολυμερών. Θα γίνει μια εισαγωγή στην έννοια του προσανατολισμού και στη μέθοδο προσδιορισμού-του με τη χρησιμοποίηση πολωμένων φασμάτων Raman. Ως αντιπροσωπευτικό παράδειγμα θα χρησιμοποιηθεί η περίπτωση του πολυ(βινυλο χλωριδίου),PVC, από μια σειρά μετρήσεων που έχουν γίνει στο εργαστήριο. Οι φοιτητές θα κληθούν να διεξάγουν μια σειρά πολωμένων φασμάτων Raman μονοαξονικά εφελκυσμένων δοκιμίων πολυ(τερεφθαλικού γλυκολεστέρα) , PET, και να δώσουν μια ποιοτική εκτίμηση του μοριακού προσανατολισμού.

Εισαγωγή

Η έννοια του προσανατολισμού, σ’ ένα εφελκυσμένο υλικό, παραπέμπει στην ταξινόμηση των δομικών-του μονάδων ως προς την κατεύθυνση εφαρμογής εξωτερικής μηχανικής παραμόρφωσης. Στην περίπτωση των πολυμερών αναφέρεται στην ευθυγράμμιση είτε πολυμερικών αλυσίδων είτε σε τμήματα αυτών ή σε ανάλογη διευθέτηση κρυσταλλικών περιοχών του πολυμερούς [1].

Η μέτρηση του μοριακού προσανατολισμού και η ποσοτικοποίησή του υπό οιαδήποτε μορφή είναι απαραίτητη προϋπόθεση για μια πληρέστερη κατανόηση της σχέσης μεταξύ του προσανατολισμού της μακρομοριακής δομής και διαφόρων μακροσκοπικών ιδιοτήτων. Η δυνατότητα διερεύνησης της ανισοτροπίας εκτεταμένων πολυμερών είναι δυνατό να προέλθει από αλληλεπίδραση του μοριακού συστήματος με ηλεκτρομαγνητική ακτινοβολία (επιλεκτική απορρόφηση πολωμένης ακτινοβολίας ή γραμμικός διχρωισμός [2,3], διπλοθλαστικότητα, σκέδαση ακτίνων Χ, σκέδαση φωτός, σκέδαση Raman [2-4]) ή από αντίστοιχη σκέδαση νετρονίων και μετρήσεις της ταχύτητας του ήχου.

Με την έννοια εφελκυσμένα πολυμερή στην παρούσα άσκηση αναφερόμαστε σε ημικρυσταλλικά πολυμερή που έχουν υποστεί μονοαξονική τάνυση υπό την επίδραση εξωτερικής μηχανικής παραμόρφωσης. Η τάνυση αυτή λαμβάνει χώρα σε υψηλότερη της υαλώδους μετάβασης θερμοκρασία (μερικές φορές κοντά και στην θερμοκρασία τήξης του πολυμερούς) και ακολουθεί άμεση ψύξη πριν την μηχανική αποφόρτιση. Κατά τον ίδιο ουσιαστικά τρόπο συνοψίζεται και η αντίστοιχη βιομηχανική διεργασία.

Τα ημι-κρυσταλλικά πολυμερή θεωρούνται ως μερικώς κρυσταλλικά όταν αποτιμώνται με μια ευαίσθητη στην κρυσταλλικότητα ιδιότητα όπως η πυκνότητα, ενώ συγχρόνως παρουσιάζουν μερικές από τις ιδιότητες που συνήθως σχετίζονται με τυχαία τακτοποίηση αλυσίδων όπως η εκτενούς σειράς (long-range) ελαστικότητα. Στην αντίστοιχη καμπύλη όγκου-θερμοκρασίας (διαστολομετρία) (Εικόνα 1) εμφανίζουν δύο μεταβολές όγκου, έναν πρώτης τάξης, της κρυσταλλοποίησης και ένα δευτέρας τάξης, της υαλώδους μετάβασης.

Εικόνα 1. Μεταβάσεις πρώτης και δευτέρας τάξης: (a) για μικρού μοριακού βάρους ενώσεις, (b) για άμορφα και ημικρυσταλλικά πολυμερή.

Στην παρούσα άσκηση, θα χρησιμοποιήσουμε πολωμένα φάσματα Raman για τον προσδιορισμό του μοριακού προσανατολισμού στερεών δοκιμίων πολυμερών μονοαξονικά εκτεταμένων σε διάφορους βαθμούς επιμήκυνσης. Ως αντιπροσωπευτικό παράδειγμα θα εξετάσουμε την περίπτωση του πολύ(βινυλο χλωριδίου), PVC. Το PVC εδώ και εξήντα χρόνια παίζει σημαντικό ρόλο στην ανάπτυξη της βιομηχανίας των πλαστικών μ’ ένα ευρύ φάσμα εφαρμογών. Ένας σημαντικός τομέας της βιομηχανίας του PVC αφορά στην παραγωγή σωλήνων πίεσης για ύδρευση και αποχέτευση. Οι μηχανικές ιδιότητες ενός τέτοιου σωλήνα βελτιώνονται με τον προσανατολισμό των μακρομοριακών αλυσίδων σε μια ή δύο διευθύνσεις μετά από κατάλληλο εφελκυσμό, ενώ ταυτόχρονα επιτυγχάνεται και μείωση του συνολικού βάρους του τελικού προϊόντος (Πίνακας 1).

Πίνακας 1:

ΣΥΓΚΡΙΤΙΚΟΣ ΠΙΝΑΚΑΣ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΣΥΜΒΑΤΙΚΩΝ ΚΑΙ ΕΦΕΛΚΥΣΜΕΝΩΝ ΠΛΑΣΤΙΚΩΝ ΣΩΛΗΝΩΝ^α

Εξωτερική διάμετρος (mm) Πίεση λειτουργίας	Φ 90 WP 6 bar		Φ 90 WP 10 bar		Φ 110 WP 6 bar		Φ 125 WP 6 bar		Επίδραση Εφελκυσμού
Είδος σωλήνα	Συμβατικ. σωλήνας	Εφελκυσμ. σωλήνας	Συμβατικ. σωλήνας	Εφελκυσμ. σωλήνας	Συμβατικ. σωλήνας	Εφελκυσμ. σωλήνας	Συμβατικ. σωλήνας	Εφελκυσμ σωλήνας	Βελτιωμένος σωλήνας
Πάχος mm	2,7	X1	4,3	X2	3,2	X3	3,7	X4
Βάρος ανά μέτρο Kg/m	1,13	0,8	1,75	1,15	1,64	1,16	2,13	1,48	30%
Βαθμός τάνυσης	-	Ψ1	-	Ψ2	-	Ψ3	-	Ψ4
Αντοχή^β σε πίεση 20^ο C: Περιφερειακή τάση/χρόνο (σ/h)	420/1	600/1 (480/ 1000)	420/1	600/1 (480/ 1000)	420/1	600/1 (450/ 1000)	420/1	550/1 (420/ 1000)	40%
Αντοχή^β σε πίεση 60^ο C: Περιφερειακή τάση/χρόνο (σ/h)	170/1 113/200	*320/1* 250/200	170/1 113/200	*310/1* 250/200	170/1 113/1	*300/1* 250/1	170/1 113/200	*280/1* 220/200	75% 120%
Αντοχή^β σε κρούση 20^οC: Θραύση δοκιμίων %	= 10	0	= 10	0	= 10	0	= 10	0	10%

WP: Water Pressure, σ = Kg/cm², h = ώρες

α Μετρήσεις βιομηχανίας πλαστικών

β Μετρήσεις βάσει διαπιστευμένων μεθόδων

Μια τέτοια φιλόδοξη προσπάθεια μεγάλης Ελληνικής Βιομηχανίας Πλαστικών για την παραγωγή εφελκυσμένων πλαστικών σωλήνων πίεσης με βελτιωμένες ιδιότητες και ταυτόχρονη μείωση βάρους του τελικού προϊόντος προσέκρουσε στην αστοχία ομοιόμορφης κατανομής των μηχανικών τους ιδιοτήτων κάτι που γίνονταν αντιληπτό μετά από καταστροφικό έλεγχο . Αυτό είχε ως αποτέλεσμα την αδυναμία διάθεσης στην αγορά ενός νέου προϊόντος. Αναζητήθηκε τότε μια ταχεία και αξιόπιστη μέθοδος αξιολόγησης του μοριακού προσανατολισμού εφελκυσμένων πολυμερών στη γραμμή παραγωγής, η οποία θα έδινε τη δυνατότητα αριστοποίησης των εμπλεκομένων παραμέτρων. Η κατανομή του μοριακού προσανατολισμού του πολυμερούς είναι αυτή που, ως αποτέλεσμα εξωτερικής μηχανικής παραμόρφωσης κατά την διεργασία μορφοποίησής του με εφελκυσμό ή εξώθηση, επηρεάζει τις μακροσκοπικές του ιδιότητες. Διεθνώς όπως προαναφέραμε χρησιμοποιούνται πολλές μέθοδοι στον προσδιορισμό του προσανατολισμού των μακρομοριακών αλυσίδων πολυμερών δοκιμίων που έχουν υποστεί εφελκυσμό. Η προσαρμογή τους όμως στην παραγωγική διαδικασία κρίνεται εξαιρετικά δύσκολη λόγω κυρίως των πολλαπλών μετρήσεων που απαιτούνται για την εξαγωγή της επιθυμητής πληροφορίας, αλλά και της αυξανόμενης πίεσης για ελαχιστοποίηση του χρόνου ανάλυσης.

Η μέθοδος που προκρίθηκε για την αντιμετώπιση του παραπάνω προβλήματος είναι η φασματοσκοπία Raman που με το χρόνο καθίσταται μια από τις ευρύτατα χρησιμοποιούμενες on line αναλυτικές τεχνικές.

Στην Εικόνα 2, απεικονίζονται σχηματικά ένα μη εφελκυσμένο, ισοτροπικό δείγμα με τις μακροαλυσίδες τυχαία κατανεμημένες στο χώρο (αριστερά) και ένα μονοαξονικά εφελκυσμένο δείγμα με τις αλυσίδες να τείνουν να προσανατολιστούν παράλληλα προς τον άξονα εφελκυσμού (δεξιά).

Για να υπάρχει κοινή γλώσσα συνεννόησης και με την βιομηχανία των πλαστικών επιλέγουμε να αντιστοιχήσουμε ένα μακροσκοπικό μέγεθος όπως ο βαθμός τάνυσης (ή εφελκυσμού) με τον προσανατολισμό των μακρομοριακών αλυσίδων.

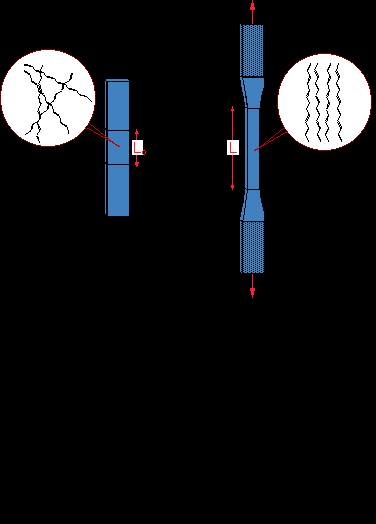
Εικόνα 2. Σχηματική απεικόνιση του βαθμού τάνυσης ενός εφελκυσμένου πολυμερούς δείγματος

Το πρωταρχικό λοιπόν ερώτημα αναφέρεται στην πιθανότητα αντιστοίχησης ενός συγκεκριμένου βαθμού εφελκυσμού σε συγκεκριμένο μακρομοριακό προσανατολισμό. Ως βαθμός εφελκυσμού ή βαθμός επιμήκυνσης, λ, ορίζεται ο λόγος του μήκους τμήματος του πολυμερούς μετά τον εφελκυσμό, L, προς το αντίστοιχο μήκος πριν τον εφελκυσμό, L_o.

Πιο συγκεκριμένα ενδιαφερόμαστε για την κατανομή του προσανατολισμού των διευθύνσεων των μακρομοριακών αξόνων ως προς έναν άξονα αναφοράς όπως αυτός του εφελκυσμού.

Για μονοαξονική συμμετρική τάνυση, ο πιο πιθανός προσανατολισμός των μακρομοριακών αλυσίδων θα είναι η ευθυγράμμισή τους κατά μήκος του άξονα εφελκυσμού με μια κατανομή αξονικής συμμετρίας γύρω απ’ αυτόν τον άξονα με ένα επίπεδο συμμετρίας κάθετο σ’ αυτόν τον άξονα. (Εικόνα 3)

Έτσι, η κατανομή του προσανατολισμού σ’ αυτήν την μονοαξονική συμμετρία εφελκυσμού

είναι δυνατόν να περιγραφεί με μια συνάρτηση Ν(θ) η οποία είναι δυνατό να περιγραφεί με μια τρισδιάστατη επιφάνεια όπου η απόσταση, r, από την αρχή των αξόνων θα δίνει την πιθανότητα μια μακρομοριακή αλυσίδα να βρεθεί σε γωνία, θ, ως προς τον άξονα αναφοράς, δηλαδή τον άξονα εφελκυσμού.

Εικόνα 3. Σχηματική αναπαράσταση μονοαξονικής συμμετρίας εφελκυσμού και αντίστοιχης συνάρτησης προσανατολισμού.

Η συνάρτηση κατανομής, Ν(θ), είναι δυνατό να αναπτυχθεί σε σειρά οι όροι της οποίας είναι πολυώνυμα Legendre. Τους σταθερούς όρους της σειράς καλούμαστε να υπολογίσουμε για να προσεγγίσουμε την κατανομή.

Με τη φασματοσκοπία Raman είναι δυνατό να προσδιορίσουμε τον δεύτερο και τον τέταρτο όρο του αναπτύγματος.

H φασματοσκοπία Raman παρέχει τη δυνατότητα άντλησης, ανεξάρτητα, της πληροφορίας που αναφέρεται στο μοριακό προσανατολισμό της άμορφης και της κρυσταλλικής φάσης ενός ημικρυσταλλικού πολυμερούς, ενώ συγχρόνως επιτρέπει τον προσδιορισμό του δεύτερου και του τέταρτου όρου του αναπτύγματος, σε πολυώνυμα Legendre, της συνάρτησης κατανομής των μακρομορίων γύρω από έναν άξονα αναφοράς όπως αυτός του εφελκυσμού. Ο πρώτος από τους δύο όρους ορίζεται ως <P2(cosθ)>=[3<cos2θ>-1]/2 και δίνει την πιθανότητα μια μακροαλυσίδα να βρεθεί υπό γωνία θ ως προς τον άξονα εφελκυσμού (αναφέρεται ως P₂), ενώ ο τελευταίος ορίζεται ως <P4(cosθ)>=[35<cos4θ>-30<cos2θ>+3]/8 και δίνει την κατανομή των μακροαλυσίδων γύρω από τη μέση αυτή γωνία θ (αναφέρεται ως P₄), επιτρέπει δηλαδή μια καλύτερη προσέγγιση της κατανομής. Αμφότερες οι παραπάνω παράμετροι είναι απαραίτητες για τον καθορισμό της συνάρτησης κατανομής προσανατολισμού και την κατανόηση των μηχανικών ιδιοτήτων εφελκυσμένων πολυμερών υπό τύπο μοριακών μοντέλων.

Πειραματικό μέρος
Τα εφελκυσμένα δείγματα του πολυ(βινυλο χλωριδίου) παρασκευάσθηκαν στο Τμήμα Μελετών Έρευνας και Ανάπτυξης της Εταιρείας Α.Γ. Πετζετάκις Α.Ε.

Η λήψη των μετρήσεων έγινε με οργανολογία micro-Raman η οποία απεικονίζεται σχηματικά στην Εικόνα 4, ενώ στη συνέχεια παρατίθεται και μια σύντομη περιγραφή των βασικών στοιχείων που την συνθέτουν:

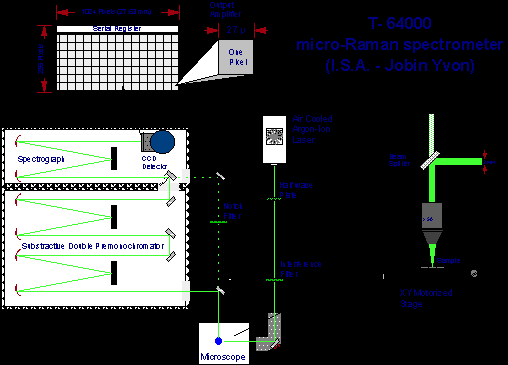
Η μονοχρωματική ακτινοβολία λ_ο=514.5 nm ενός γραμμικά πολωμένου αερόψυκτου laser ιόντων αργού (μοντέλο 163-Α42 της Spectra Physics) κατευθύνεται μέσω ενός πλακιδίου καθυστέρησης φάσης λ/2 (half-wave plate) – το οποίο δίνει τη δυνατότητα επιλογής της πόλωσης του laser- και ενός φίλτρου στενής φασματικής διαπερατότητας της διεγείρουσας ακτινοβολίας (interference filter) – για την αποβολή των παρασιτικών γραμμών εκπομπής του αργού - στο χώρο υποδοχής ενός διαμορφωμένου για μετρήσεις οπισθοσκέδασης Raman μικροσκοπίου. Η ισχύς του laser επί των δειγμάτων είναι της τάξης των 1-3 mW. Στο μικροσκόπιο, η προώθηση της δέσμης του laser και η συλλογή της σκεδαζόμενης ακτινοβολίας γίνεται μέσω ενός διαχωριστή δέσμης (beamsplitter) και ενός αντικειμενικού φακού x50 Olympus μεγάλης εστιακής απόστασης (8mm). Η σκεδαζόμενη ακτινοβολία μετά την ανάλυσή της εστιάζεται στη σχισμή εισόδου ενός τριπλού μονοχρωμάτορα (Τ-64000, Jobin Yvon) όπου τα φωτόνια Raman διασπείρονται και ανιχνεύονται με τη βοήθεια ενός CCD συστήματος (Spectraview 2D) ψυχωμένου στους 140 Κ.

Εικόνα 4. Οργανολογία micro-Raman

Γεωμετρία σκέδασης

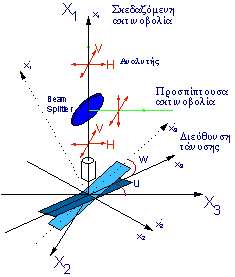
Για τον ποσοτικό προσδιορισμό του μοριακού προσανατολισμού εφελκυσμένων πολυμερών δειγμάτων με σκέδαση Raman υιοθετήσαμε την ανάλυση του Bower [5] την οποία και προσαρμόσαμε σε γεωμετρία οπισθοσκέδασης όπως αυτή του micro-Raman. Ορίζουμε λοιπόν δύο συστήματα καρτεσιανών συντεταγμένων, το ένα σταθερά προσαρμοσμένο στο πολυμερές δείγμα, Ox₁x₂x₃, (ή Ox’₁x’₂x’₃ όταν το δοκίμιο είναι κεκλιμένο κατά μια γωνία w όπως φαίνεται στην Εικ. 1) και το άλλο προσαρμοσμένο στο εργαστήριο και στις πειραματικές διατάξεις που χρησιμοποιούνται, OX₁X₂X₃ (Εικ. 2).

Εικόνα 5. Πειραματική διάταξη και άξονες συντεταγμένων για τη μελέτη του μοριακού προσανατολισμού εφελκυσμένων πολυμερών με γεωμετρία 180^ο σκέδασης Raman

Ο συμβολισμός μιας μέτρησης πολωμένου φάσματος Raman περιλαμβάνει ένα συνδυασμό τριών γραμμάτων, όπως h-VV. Το πρώτο μικρό επικλινές γράμμα, όπως h, v, d ή s, υποδηλώνει τον προσανατολισμό του άξονα εφελκυσμού Ox₃ (w=0^o) ή Ox₃^’ (w¹ 0^o) ως προς το προσαρμοσμένο στο εργαστήριο σύστημα καρτεσιανών συντεταγμένων, OX₁X₂X₃: h, όταν είναι παράλληλος ως προς τον άξονα OX₃ (u=0^o & w=0^o), v, όταν είναι παράλληλος ως προς τον άξονα OX₂ (u=90^o & w=0^o), d, όταν είναι παράλληλος ως προς τη διχοτόμο της γωνίας X₃OX₂ (u=45^o& w=0^o), και s, όταν είναι παράλληλος ως προς τον άξονα OX₁(w=90^o). Τα υπόλοιπα δύο κεφαλαία γράμματα, όπως HH, HV, VV or VH, υποδηλώνουν σε κάθε περίπτωση την κατεύθυνση πόλωσης της διεγείρουσας και σκεδαζόμενης ακτινοβολίας αντίστοιχα: H, όταν η πόλωση είναι παράλληλη προς τον άξονα OX₃ και V, όταν η πόλωση είναι παράλληλη προς τον άξονα OX₂.

Με τη φασματοσκοπία Raman μελετούμε τον προσανατολισμό μιας συγκεκριμένης κανονικής μορφής δόνησης ενός τμήματος της μακροαλυσίδας ή μιας θεμελιώδους ομάδας του πολυμερούς. Θεωρούμε δε ότι ο προσανατολισμός των δομικών αυτών στοιχείων δίνει κατ΄ αναλογία και τον μοριακό προσανατολισμό των μακροαλυσίδων. Στις περισσότερες των περιπτώσεων επιλέγουμε συμμετρικές δονήσεις τάσης σκελετικών κανονικών μορφών δόνησης όπως αυτή του παρα-υποκαταστημένου φαινυλίου στην περίπτωση του PET ή της all-trans συζυγίας διπλών δεσμών στην περίπτωση του υποβαθμισμένου PVC. Οι σκελετικές αυτές δονήσεις τάσης παρουσιάζουν μεταβολή πολωσιμότητας σε παράλληλη προς τη ανάπτυξη των μακροαλυσίδων διεύθυνση. Στην ίδια διεύθυνση θα παρουσιάζουν και αυξημένη πιθανότητα ενεργότητας Raman. Αυτό ακριβώς είναι το στοιχείο που χρησιμοποιούμε για την ποιοτική και ποσοτική εκτίμηση του μοριακού προσανατολισμού εφελκυσμένων πολυμερικών δοκιμίων κατευθύνοντας ανάλογα το κυματάνυσμα του ηλεκτρικού πεδίου της διεγείρουσας ακτινοβολίας laser σε συνδυασμό πάντα με κατάλληλη ανάλυση της σκεδαζόμενης ακτινοβολίας. Εφ’ όσον το κυματάνυσμα του ηλεκτρικού πεδίου του laser είναι παράλληλο προς την διεύθυνση μεταβολής της πολωσιμότητας μιας κανονικής μορφής δόνησης τότε υπάρχει αυξημένη πιθανότητα ενεργότητας Raman, δηλαδή πιθανότητα ισχυρής ανελαστικής σκέδασης Raman.

Θεωρία προσδιορισμού του μοριακού προσανατολισμού με πολωμένα φάσματα Raman

Η συνολική ένταση της σκεδαζόμενης ακτινοβολίας Raman δίδεται από τη σχέση:

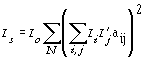(1)

Ι_i και Ι_j’ είναι τα συνημίτονα κατεύθυνσης της πόλωσης του προσπίπτοντος και του σκεδαζόμενου φωτός ως προς το σύστημα συντεταγμένων του δείγματος.

I_o είναι μια σταθερά που εξαρτάται από την ένταση της προσπίπτουσας ακτινοβολίας και πειραματικές παραμέτρους.

Κάθε a_ij όρος είναι δυνατόν να εκφραστεί ως ένας γραμμικός συνδυασμός των κύριων στοιχείων a₁, a₂ και a₃ του τανυστή πολωσιμότητας της μελετούμενης κανονικής μορφής δόνησης και των γωνιών Euler που καθορίζουν τον προσανατολισμό των κυρίων αξόνων του τανυστή ως προς τις συντεταγμένες που έχουν προσαρμοστεί στο δείγμα, Ox₁x₂x₃.

Οι πειραματικές τιμές είναι της μορφής I_oκαι καθώς το άθροισμα υπονοεί ότι όλες οι μονάδες σκέδασης, που συνεισφέρουν στην ένταση της σκεδαζόμενης ακτινοβολίας που παρατηρούμε, λαμβάνονται υπ΄ όψη, οι τιμές αυτές εμπεριέχουν πληροφορίες για την κατανομή του προσανατολισμού αυτών των δομικών μονάδων.

Στην περίπτωση μονοαξονικής στατιστικής συμμετρίας με μη προτιμητέο προσανατολισμό γύρω από τον κύριο μοριακό άξονα της θεωρούμενης δομικής μονάδας της μακροαλυσίδας και όταν οι άξονες του τανυστή συμπίπτουν με τους δομικούς μοναδιαίους άξονες (άξονες συμμετρίας της δομικής μονάδας) μπορούμε να γράψουμε :

(2)

Ν_ο είναι ο αριθμός των δομικών μονάδων (αριθμός σκεδαστών) που συνεισφέρουν στην ένταση Raman.

A_l00^ijpq είναι συναρτήσεις δευτέρας τάξεως των a₁,a₂,a₃ όρων του διαγωνιοποιημένου τανυστή Raman για συγκεκριμένη κανονική μορφή δόνησης που καθορίζεται από τους δομικούς άξονες συμμετρίας (οι συναρτήσεις έχουν καταγραφεί [5]).

M_l00 χαρακτηρίζει την κατανομή του προσανατολισμού του συνόλου των δομικών μονάδων που είναι διεγερμένες στη θεωρούμενη κανονική μορφή δόνησης και εκφράζεται υπό όρους πολυώνυμων Legendre : M_l00=(1/4π²){(2λ+1)/2}^½<P_l(cosθ)> (l=0,2,4)

θ είναι η γωνία μεταξύ του κύριου μοριακού άξονα της θεωρούμενης δομικής μονάδας και του προσαρμοσμένου επί του δοκιμίου άξονα κατά την διεύθυνση της τάνυσής του, Ox₃.

Για πολυμερές δείγμα με μονοαξονική συμμετρία υπάρχουν μόνο πέντε ανεξάρτητα μη μηδενικά αθροίσματα της μορφής:

τα οποία συνδέονται με πειραματικές μετρήσεις έντασης σκέδασης Raman σε διάφορους προσανατολισμούς δείγματος και γεωμετρίες πόλωσης .

Αν Ι_ij είναι η ένταση της σκεδαζόμενης ακτινοβολίας όταν η προσπίπτουσα είναι πολωμένη παράλληλα προς τον i άξονα και η σκεδαζόμενη πολωμένη παράλληλα προς τον j άξονα του προσαρμοσμένου στο εργαστήριο OX₁X₂X₃συστήματος τότε :

(3a)

(3b)

(3c)

(3d)

(3e)

Η επίλυση-σύγκλιση αυτών των εξισώσεων, με την επιβαλλόμενη διεξαγωγή πέντε ανεξάρτητων μετρήσεων για κάθε δείγμα, επιτρέπει τον προσδιορισμό των πέντε αγνώστων μεταξύ των οποίων είναι τα y = <P₂(cosθ)>/b, z = <P₄(cosθ)>/b (οι άλλοι τρεις άγνωστοι είναι x = b (πειραματική σταθερά = Ι_οΝ_οa₃²), α₁ = a₁/a₃ και α₂= a₂/a₃).

R₁ ως R₇ είναι πολυώνυμα δεύτερης τάξης εξαρτώμενα από τα α₁ και α₂.

Εκτίμηση του μοριακού προσανατολισμού με πολωμένα φάσματα Raman

Ας εξετάσουμε το φάσμα Raman του PVC που απεικονίζεται στο Σχήμα 1. Τα κύρια χαρακτηριστικά του δονητικού φάσματος της πρώτης ύλης, του καθαρού PVC (στο κάτω Σχήμα 1: Φάσματα Raman καθαρού PVC (πρώτης ύλης) και βιομηχανικών δειγμάτων PVC.

μέρος του Σχ. 1) εντοπίζονται σε δύο περιοχές συχνοτήτων σκέδασης. Στην περιοχή χαμηλών συχνοτήτων, στους ~650 cm^-1, παρατηρούμε τη συχνότητα τάσης C-Cl, ενώ σε υψηλότερες συχνότητες, στους ~1430 cm^-1, τη συχνότητα κάμψης του CH₂.

Στο φάσμα Raman όμως ενός βιομηχανικού δείγματος PVC (στο μεσαίο & πάνω μέρος του Σχ.1.) εμφανίζονται δύο νέες κορυφές δόνησης στους 1127 και 1515 cm^-1 αντίστοιχα, που αποδίδονται στην ύπαρξη συζυγών διπλών δεσμών εξ αιτίας αφυδροχλωρίωσης που προκαλείται από θερμική υποβάθμιση.

~(CH₂CHCl)_n~ ~(CH₂CHCl)_m-(CH=CH)_n-m~ + (n-m) HCl

Η θερμική υποβάθμιση του PVC λαμβάνει χώρα κατά την προετοιμασία δειγμάτων, όπως και κατά την βιομηχανική διεργασία παραγωγής προϊόντων PVC.

Είναι χαρακτηριστικό ότι ενώ η συγκέντρωση των συζυγών διπλών δεσμών είναι της τάξης του 0.1 ανά 1000 βινυλοχλωρίδια, οι αντίστοιχες κορυφές Raman είναι συγκρίσιμες ή ακόμη και μεγαλύτερες από αυτές του PVC (πάνω μέρος του Σχ. 1.). Αυτό οφείλεται, κατά ένα βαθμό στην ιδιαιτερότητα της συγκεκριμένης δόνησης των συζυγών διπλών δεσμών λόγω της διάσπαρτης ηλεκτρονιακής κυματοσυνάρτησης κατά μήκος τους, αλλά κυρίως διότι η δόνηση αυτή για το μήκος κύματος της ακτινοβολίας που χρησιμοποιήθηκε (514.5 nm) έδωσε φάσμα Raman συντονισμού. Η διεγείρουσα δηλαδή ακτινοβολία laser που χρησιμοποιήθηκε, ν_ο, ήταν μέσα στη ζώνη απορρόφησης, ν_e συγκεκριμένης συζυγίας διπλών δεσμών. (Βλέπε Παράρτημα 1)

Οι all-trans διαμόρφωσης συζυγείς διπλοί δεσμοί είναι ραβδόμορφα (rod-like) σκελετικά τμήματα των μακροαλυσίδων του PVC, ανεξάρτητα των διαμορφώσεων της μικροδομής του ίδιου του PVC, με ισχυρή λόγω συντονισμού σκέδαση Raman και βρίσκονται κυρίως στην άμορφη φάση του πολυμερούς. Ο προσανατολισμός τους μπορεί να θεωρηθεί ότι χαρακτηρίζει, έστω και κατ’ αναλογία, τον προσανατολισμό των μακρομορίων της άμορφης φάσης του PVC. Ως γνωστό, το PVC είναι κατά βάση άμορφο πολυμερές με βαθμό κρυσταλλικότητας ~ 10%.

Αυτό λοιπόν το εγγενές για την τεχνολογία του PVC πρόβλημα σκεφτήκαμε να εξετάσουμε αν μπορούμε να το χρησιμοποιήσουμε ως ενδείκτη για τον προσδιορισμό του μοριακού προσανατολισμού του PVC.

Στο Σχήμα 2 απεικονίζονται τα πολωμένα φάσματα Raman ενός εφελκυσμένου και ενός μη εφελκυσμένου βιομηχανικού δείγματος PVC στην περιοχή συχνοτήτων τάσης των συζυγών διπλών δεσμών. Οι χαρακτηριστικές ζώνες σκέδασης που εμφανίζουν κάποιου είδους εξάρτηση από τη διαδικασία εφελκυσμού είναι: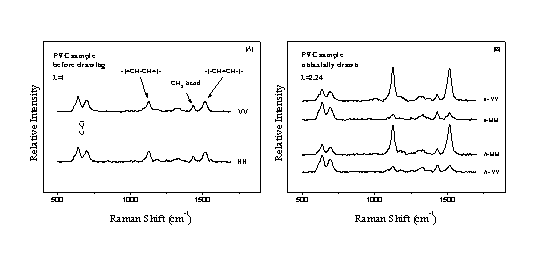

η C-Cl συμμετρική δόνηση τάσης στις χαμηλές συχνότητες (εγκάρσια, ως προς την διεύθυνση ανάπτυξης της μακροαλυσίδας, δόνηση),

η CH₂ δόνηση κάμψης στους 1432 cm^-1 και

οι σκελετικές δονήσεις τάσης συστοιχιών συζυγών διπλών δεσμών στους 1127 και 1515 cm^-1

Σχήμα 2: Πολωμένα φάσματα Raman ενός μη εφελκυσμένου (αριστερά) και ενός μονοαξονικά εφελκυσμένου (δεξιά) βιομηχανικού δοκιμίου PVC.

Πιο συγκεκριμένα στα πολωμένα φάσματα Raman του μη εφελκυσμένου δείγματος (στο αριστερό μέρος του Σχ. 2) δεν παρατηρείται οιαδήποτε διαφοροποίηση λόγω προσανατολισμού δείγματος ή χρησιμοποιηθείσας γεωμετρίας πόλωσης. Αυτό οφείλεται στον μη προτιμητέο (τυχαίο) προσανατολισμό των μακροαλυσίδων και κατά συνέπεια και των παραπάνω δομικών ειδών, καθότι το δοκίμιο είναι ισοτροπικό.

Στα πολωμένα όμως φάσματα Raman του εφελκυσμένου PVC δείγματος (στο δεξιό μέρος του Σχ. 2) παρατηρούνται αξιοσημείωτες μεταβολές. Η έκταση αυτών των μεταβολών εξαρτάται από την θέση του δοκιμίου, v ή h, σε σχέση με το προσαρμοσμένο στο εργαστήριο σύστημα συντεταγμένων (βλέπε Εικόνα 5), αντικατοπτρίζει δε την επαγόμενη από τη διαδικασία εφελκυσμού ανισοτροπία. Η ένταση της κορυφής δόνησης τάσης του C-Cl, η οποία είναι κατά το μάλλον ή ήττον κάθετη στον άξονα των μακρομοριακών αλυσίδων, όπως και η μεταβολή πολωσιμότητάς της, αυξάνεται στις γεωμετρίες πόλωσης που είναι κάθετες στον προσανατολισμό του δοκιμίου και κατά συνέπεια κάθετες και στον άξονα εφελκυσμού (v-HH & h-VV). Απεναντίας, οι κορυφές δόνησης τάσης των σκελετικών πολυενίων αυξάνονται σε μεγάλο βαθμό στις παράλληλες προς την διεύθυνση εφελκυσμού γεωμετρίες πόλωσης (v-VV & h-HH). Επιπλέον αξίζει να σημειωθεί η συμπεριφορά της δόνησης κάμψης του μεθυλενίου. Η ένταση της σκεδαζόμενης ακτινοβολίας αυτής της κανονικής μορφής δόνησης του PVC δείχνει να μην επηρεάζεται από γεωμετρία πόλωσης και προσανατολισμό δοκιμίου, υποδηλώνοντας ελάχιστη ευαισθησία στον επαγόμενο μοριακό προσανατολισμό.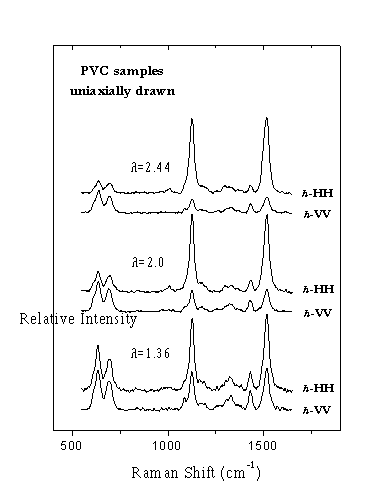

Στο Σχήμα 3 απεικονίζονται ζεύγη πολωμένων φασμάτων Raman, h-HH και h-VV, για δοκίμια PVC σε διάφορους βαθμούς εφελκυσμού.

Σχήμα 3. Πολωμένα φάσματα Raman, h-HH και h-VV, δοκιμίων PVC μονοαξονικά εφελκυσμένων σε διάφορους βαθμού εφελκυσμού

Για την διευκόλυνση όποιας σύγκρισης τα φάσματα έχουν κανονικοποιηθεί ώστε η ένταση της κορυφής στους 1515 cm^-1 να είναι η ίδια σ’ όλα τα φάσματα h-HH. Κατ΄ αυτό τον τρόπο η ένταση αυτής κορυφής (στους 1515 cm^-1) στην κάθετη ως προς τον άξονα εφελκυσμού γεωμετρία πόλωσης, h-VV, εμφανίζει μια σαφή πτώση με την αύξηση του μακροσκοπικού βαθμού εφελκυσμού κάτι που υποδηλώνει μία κατ’ αναλογία αύξηση του μοριακού προσανατολισμού. Η δεύτερη κορυφή των σκελετικών πολυενίων στους 1127 cm^-1 εμφανίζει την ίδια συμπεριφορά. Επιπλέον στο ίδιο Σχήμα μπορούμε να παρατηρήσουμε ότι η δόνηση κάμψης του CH₂ στους 1432 cm^-1 παραμένει πρακτικά ανεξάρτητη της γεωμετρίας πόλωσης. Επίσης η σχετική ένταση της C-Cl κορυφής στους ~650 cm^-1 στην παράλληλη προς τον άξονα εφελκυσμού γεωμετρία πόλωσης, h-HH, παρουσιάζει μία σταδιακή μείωση αυξανομένου του βαθμού εφελκυσμού.

Η παραπάνω συμπεριφορά των κορυφών Raman είναι δυνατό να ποσοτικοποιηθεί με την εισαγωγή του “βαθμού αποπόλωσης”, h-HH/h-VV, ο οποίος και δίνεται στο Σχήμα 4 συναρτήσει του βαθμού εφελκυσμού, λ. Είναι προφανές ότι ο “βαθμός αποπόλωσης” της κορυφής δόνησης του CH₂ κάμψης είναι σχεδόν ανεξάρτητος του βαθμού εφελκυσμού, ενώ η C-Cl δόνηση τάσης εμφανίζει μία μικρή εξάρτηση από τον βαθμό εφελκυσμού. Ο λόγος h-HH/h-VV της κορυφής συζυγιών διπλών δεσμών στους 1515 cm^-1 επηρεάζεται πολύ από το λ, αναδεικνύοντας την αυξημένη ευαισθησία τους στον μοριακό προσανατολισμό που επάγεται με τον εφελκυσμό.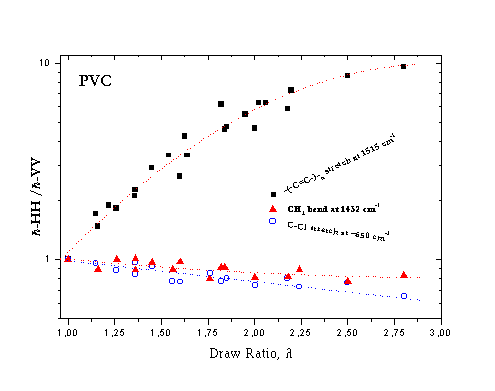

Σχήμα 4. Ο “βαθμός αποπόλωσης”, h-HH/h-VV, συναρτήσει του βαθμού εφελκυσμού, λ, για μονοαξονικά εφελκυσμένα δοκίμια PVC.

Σημειώνουμε ότι ένας “βαθμός αποπόλωσης”, h-HH/h-VV, μικρότερος της μονάδας για μια κανονική μορφή δόνησης με μεταβολή πολωσιμότητας κατά το μάλλον ή ήττον κάθετα στον άξονα εφελκυσμού, καθώς επίσης και ένας “βαθμός αποπόλωσης”, h-HH/h-VV, μεγαλύτερος της μονάδας για μια κανονική μορφή δόνησης με μεταβολή πολωσιμότητας κατά το μάλλον ή ήττον παράλληλα στη διεύθυνση εφελκυσμού υποδεικνύουν αμφότεροι ένα βαθμό μοριακού προσανατολισμού.

Λαμβάνοντας τέλος υπ’ όψη τη θεωρία προσδιορισμού του μοριακού προσανατολισμού που αναπτύξαμε προηγουμένως, με μία σειρά πολωμένων φασμάτων Raman σε διάφορες γεωμετρίες πόλωσης και προσανατολισμού δείγματος υπολογίζουμε τους <P2(cosθ)> και <P4(cosθ)> όρους του αναπτύγματος της συνάρτησης προσανατολισμού. Τα P2 και P4 δίνονται στο Σχήμα 5 συναρτήσει του βαθμού εφελκυσμού για τις δύο σκελετικές κορυφές δόνησης των συζυγών διπλών δεσμών στους 1127 και 1515 cm^-1και δείχνουν να ακολουθούν την τάση που παρουσίασε ο αντίστοιχος “βαθμός αποπόλωσης”, h-HH/h-VV, για την κορυφή στους 1515 cm^-1 του Σχήματος 4.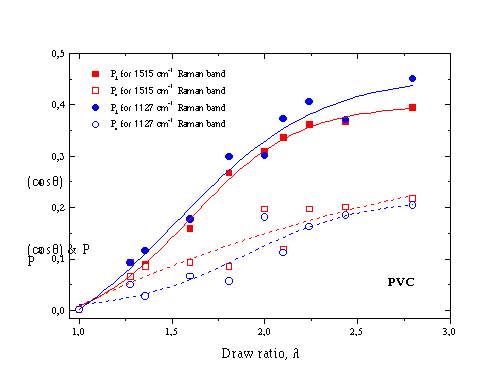

Σχήμα 5. Ο δεύτερος, P2, και ο τέταρτος, P4, όρος του αναπτύγματος της συνάρτησης κατανομής προσανατολισμού για τις σκελετικές δονήσεις τάσης των συζυγών διπλών δεσμών συναρτήσει του βαθμού εφελκυσμού, λ.

Στο Σχήμα 5 φαίνεται η εξάρτηση των P₂ & P₄, που υπολογίσθηκαν και για τις δύο δονήσεις τάσης των συζυγών διπλών δεσμών, από τον βαθμό εφελκυσμού και παρατηρούμε ότι αυξανομένου του βαθμού επιμήκυνσης αυξάνεται και ο μοριακός προσανατολισμός.

Ο υπολογισμός των P2 και P4 δεν δίδεται πιο διεξοδικά διότι θεωρούμε ότι θα ξεφύγουμε από τις βασική επιδίωξη να καταδείξουμε την χρησιμότητα των πολωμένων φασμάτων Raman στην εκτίμηση του μοριακού προσανατολισμού εφελκυσμένων πολυμερών.

Ταχεία εκτίμηση μοριακού προσανατολισμού βινυλικών πολυμερών με ένα πολωμένο φάσμα Raman

Παρά το γεγονός ότι έμμεσα επιλύθηκε το πρόβλημα του μοριακού προσανατολισμού του PVC η μέτρηση στη γραμμή παραγωγής που στην αρχή θέσαμε ως προϋπόθεση προσέγγισης του βιομηχανικού προβλήματος συνεχίζει να θεωρείται ανέφικτη λόγω των πολλών απαιτούμενων μετρήσεων Raman σε διάφορες γεωμετρίες πόλωσης.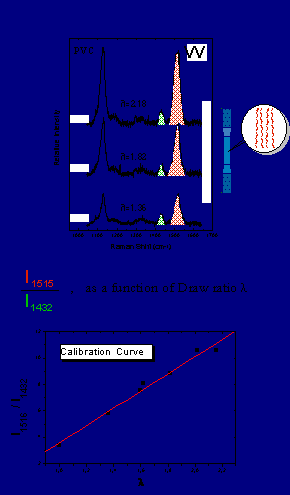

Ας επανέλθουμε όμως στην παρατήρησή μας ότι η κορυφή στους 1432 cm^-1, που αποδίδεται στην CH₂ δόνηση κάμψης του PVC, δείχνει να μην είναι ευαίσθητη στον εφελκυσμό. Θα ήταν δυνατό λοιπόν από μερικά “πρότυπα” βιομηχανικά δείγματα σε διάφορους βαθμούς εφελκυσμού να προσδιοριστούν στο εργαστήριο τα αντίστοιχα <P₂(cosθ)> και κατόπιν να σχεδιαστεί μια καμπύλη βαθμονόμησης που να περιλαμβάνει το λόγο των εμβαδών δύο κορυφών Raman (σε μια γεωμετρία πόλωσης), μίας ευαίσθητης στον προσανατολισμό (η κανονική μορφή δόνησης των συζυγών διπλών δεσμών στους 1515 cm^-1) και μιας μη-ευαίσθητης στον προσανατολισμό (η αποπολωμένη εγγενής κανονική μορφή δόνησης του PVC στους 1432 cm^-1) σαν συνάρτηση του <P₂(cosθ)> που θα έχουμε υπολογίσει (ή κατ’ αντιστοιχία σαν συνάρτηση του βαθμού εφελκυσμού, λ).

Σχήμα 6: Αντιπροσωπευτικά φάσματα Raman βιομηχανικών δοκιμίων PVC μονοαξονικά εφελκυσμένων σε διάφορους βαθμούς επιμήκυνσης σε συγκεκριμένο προσανατολισμό δείγματος και γεωμετρία πόλωσης (επάνω). Καμπύλη βαθμονόμησης (κάτω).

Στη γραμμή παραγωγής θα αρκούσε η λήψη ενός φάσματος Raman σε κατάλληλη γεωμετρία πόλωσης. Μέσω υπολογιστή, τα εμβαδά των δύο κορυφών και κατά συνέπεια ο λόγος τους θα έδινε αυτόματα δια της καμπύλης βαθμονόμησης τον προσανατολισμό των μακρομορίων. Το αποτέλεσμα των παραπάνω συλλογισμών όσον αφορά τουλάχιστον στην κατασκευή της καμπύλης βαθμονόμησης απεικονίζονται στο Σχήμα 6.

Για την επίλυση του συνολικού προβλήματος απαιτείται εξειδικευμένη ευέλικτη οργανολογία Raman η οποία βασίζεται στην micro-Raman διαμόρφωση. Η σχεδίαση της παραπάνω ευέλικτης οργανολογίας υπήρξε προϊόν συνεργασίας της ερευνητικής μας ομάδας, του βιομηχανικού εταίρου, και μιας πρωτοπόρου στη σχεδίαση οργανολογιών Raman Ευρωπαϊκής Εταιρείας, ενώ καθοριστικής σημασίας ήταν η οικονομική βοήθεια της ΓΓΕΤ μέσω ενός προγράμματος ΑΧΙΑ-11.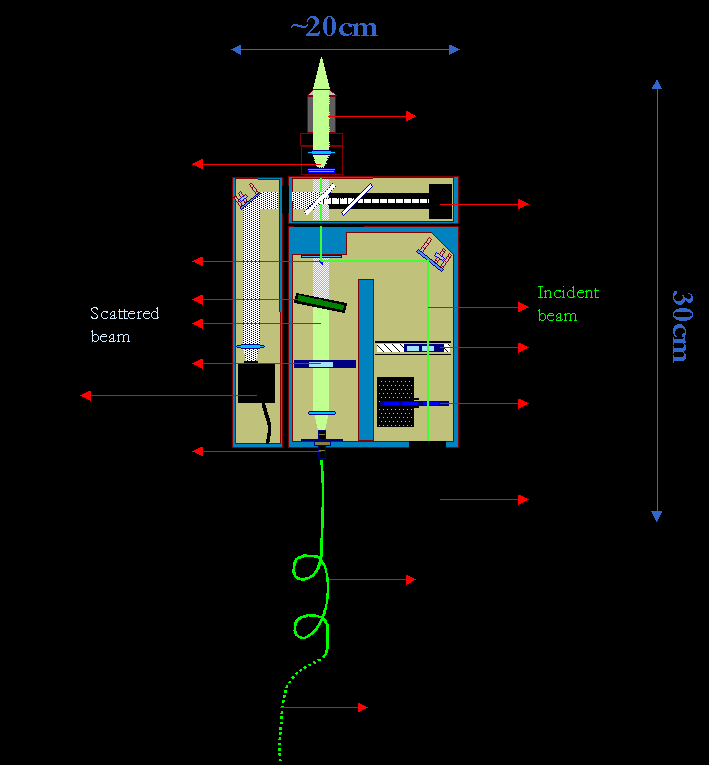

Η ευέλικτη αυτή οργανολογία Raman απεικονίζεται στην Εικόνα 6 όπου αναγράφονται και όλα τα στοιχεία που την συνθέτουν.

Εικόνα 6. Ευέλικτη οργανολογία Raman

ΑΣΚΗΣΗ

Οι φοιτητές θα έχουν την ευκαιρία να χρησιμοποιήσουν είτε την κλασσική micro-Raman οργανολογία είτε την ευέλικτη οργανολογία με την micro-Raman κεφαλή. Αυτό θα εξαρτηθεί από το εάν η τελευταία θα έχει ήδη μετακινηθεί στη γραμμή παραγωγής συγκεκριμένης βιομηχανικής μονάδας.

Εν πάση περιπτώσει, οι φοιτητές θα έχουν την ευκαιρία λήψης πολωμένων φασμάτων Raman εφελκυσμένων δοκιμίων πολυ(τερεφθαλικού γλυκολεστέρα), PET.

Παρασκευή δοκιμίων
H παρασκευή δοκιμίων PET από εμπορική πρώτη ύλη έγινε στο εργαστήριο. Η ανάπτυξη των υμενίων, πάχους 35-40 μm, έγινε με τήξη και συμπίεση του υλικού μεταξύ πλακών Teflon σε θερμοκρασία 300 ⁰C. Στη συνέχεια, τεμάχια του αρχικού υμενίου υπέστησαν εφελκυσμό σε θερμοκρασία 84 ⁰C (Τ_g=74 ⁰C) και με ταχύτητα 12 cm/min. Με την μέθοδο αυτή προέκυψαν δοκίμια ΡΕΤ με διάφορους βαθμούς εφελκυσμού.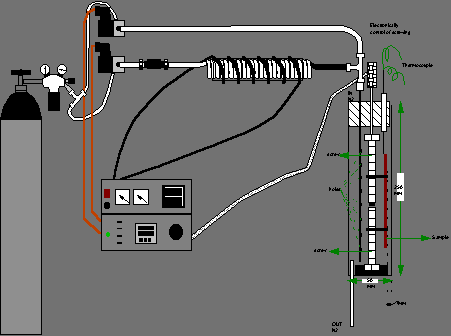

Ο μονοαξονικός εφελκυσμός των δοκιμίων λαμβάνει χώρα στο στοιχείο εφελκυσμού που φαίνεται στην Εικόνα 7 και έχει κατασκευαστεί από την Τεχνική Υπηρεσία του ΕΙΧΗΜΥΘ/ΙΤΕ.

Εικόνα 7. Στοιχείο εφελκυσμού

Το δοκίμιο πιάνεται σε δύο στηρίγματα των οποίων τα άλλα άκρα έχουν οπές παξιμαδιού που μπορεί να βιδώνουν και να ξεβιδώνουν ελεύθερα σε ένα άξονα με ανάστροφο σπείρωμα. Από τη μέση και πάνω, όπου προσαρτάται το ένα στήριγμα, ο άξονας έχει δεξιόστροφο σπείρωμα και από τη μέση και κάτω, όπου προσαρτάται το άλλο στήριγμα έχει αριστερόστροφο σπείρωμα. Περιστρέφοντας κατάλληλα τον άξονα με ένα μοτέρ τα δύο στηρίγματα απομακρύνονται και προκαλείται μονοαξονικός εφελκυσμός στα προσαρμοσμένα δοκίμια. Η εξασφάλιση της επιθυμητής θερμοκρασίας γίνεται με τη διοχέτευση στον χώρο υποδοχής δείγματος προθερμαινόμενου σε ένα φούρνο αντίστασης αζώτου. Η θερμοκρασία ελέγχεται στο χώρο του δείγματος, όπως επίσης ηλεκτρονικά ελέγχονται ο ρυθμός τάνυσης καθώς και ο βαθμός τάνυσης. Όταν το δοκίμιο εφελκυστεί στον προεπιλεγμένο βαθμό τάνυσης, μια αυτόματη εναλλαγή βαλβίδων επιτρέπει την διοχέτευση ψυχρού αζώτου στο χώρο υποδοχής δείγματος για τη διατήρηση του μοριακού προσανατολισμού που έχει ήδη επιτευχθεί.

Στην περίπτωση χρησιμοποίησης της ευέλικτης οργανολογίας Raman το στοιχείο εφελκυσμού θα προσαρμοστεί στην κεφαλή Raman και θα ληφθούν on line μετρήσεις πολωμένων φασμάτων Raman. Στην περίπτωση αυτή με ένα μη εφελκυσμένο δοκίμιο θα είναι δυνατό να γίνουν όλες οι προβλεπόμενες μετρήσεις σε διάφορους σταδιακά αυξανόμενους βαθμούς εφελκυσμού.

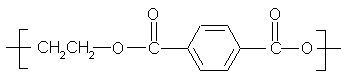
Εικόνα 8. Η δομική μονάδα του πολυ(τερεφθαλικού γλυκολεστέρα) (αριστερά) και η συμμετρική δόνηση τάσης του 1,4 παρα-υποκατεστημένου βενζολίου (δεξιά).

Στην εικόνα 8 απεικονίζεται η δομική μονάδα του πολυ(τερεφθαλικού γλυκολεστέρα), PET και η συμμετρική δόνηση τάσης του 1,4 παρα-υποκατεστημένου βενζολίου. Η κανονική μορφή αυτή δόνησης με συχνότητα Raman γύρω στους 1616 cm^-1 είναι μια σκελετική δόνηση με μεταβολή πολωσιμότητας παράλληλη με την διεύθυνση ανάπτυξης των μακροαλυσίδων, τη διεύθυνση του άξονα εφελκυσμού.

Αποτελέσματα

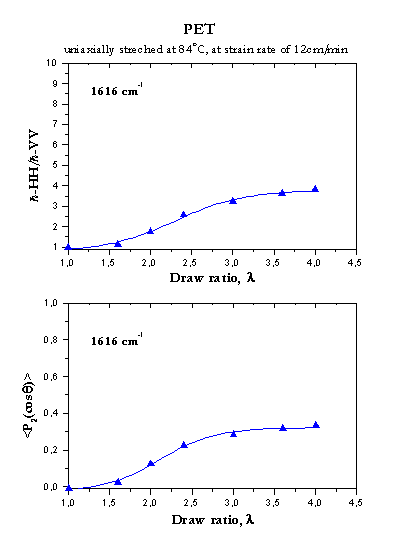
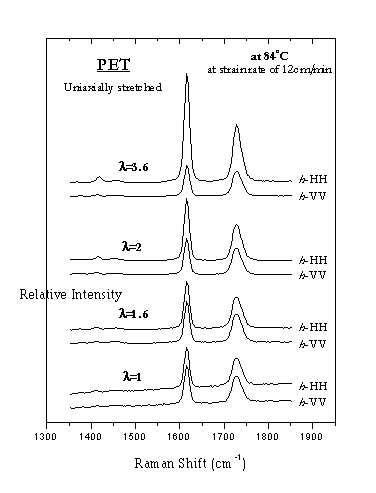
Στα παρακάτω σχήματα δίδονται συνοπτικά τα αποτελέσματα μετρήσεων για την εκτίμηση του μοριακού προσανατολισμού μονοαξονικά εφελκυσμένων δοκιμίων PET που έχουν ληφθεί με την ευέλικτη οργανολογία Raman.

Σχήμα 7. (Αριστερά) Πολωμένα φάσματα Raman, h-HH και h-VV, δοκιμίων PET μονοαξονικά εφελκυσμένα σε διάφορους βαθμούς εφελκυσμού.

Σχήμα 8. (Δεξιά) Ο “βαθμός αποπόλωσης”, h-HH/h-VV, για τη σκελετική δόνηση τάσης του 1,4 παρα-υποκατεστημένου φαινυλίου συναρτήσει του βαθμού εφελκυσμού, λ, για μονοαξονικά εφελκυσμένα δοκίμια PET (επάνω). Ο δεύτερος, P2,, όρος του αναπτύγματος της συνάρτησης κατανομής προσανατολισμού για τη σκελετική δόνηση τάσης του 1,4 παρα-υποκατεστημένου φαινυλίου συναρτήσει του βαθμού εφελκυσμού, λ (κάτω).

Ανάλογες μετρήσεις μ’ αυτές που έδωσαν τα παραπάνω αποτελέσματα θα κληθούν να διεξάγουν και οι φοιτητές του προγράμματος.

Ευχαριστίες

Ευχαριστούμε θερμά τους Μεταπτυχιακούς Υποτρόφους του ΕΙΧΗΜΥΘ-ΙΤΕ και Υποψηφίους Διδάκτορες του Τμήματος Χημ. Μηχανικών του Πανεπιστημίου Πατρών Amaia Soto και Κων/ντίνο Ανδρικόπουλο για την βοήθεια που προσέφεραν στην ολοκλήρωση των παραπάνω εργαστηριακών ασκήσεων.

Βιβλιογραφικές Αναφορές

1. Ward I. M. Developments in Oriented Polymers - I , II; Applied Science Publishers: London, 1982; Ward I. M. Advances in Polymer Science, vol. 66, p.81, Springer-Verlag: Berlin, 1985; Ward I.M. Structure and Properties of Oriented Polymers, Chapman & Hall, London, 1997

2. Voyiatzis, G.; Petekidis, G.; Vlassopoulos, D.; Kamitsos, E. I.; Bruggeman, A. Macromolecules 1996, 29, 2244.

3. Andrikopoulos, K.; Vlassopoulos, D.; Voyiatzis,G.A.; Yiannopoulos, Y.D.;

Kamitsos, E.I., Macromolecules 1998, 31, 5465.

4. Deimede, V.; Andrikopoulos, K.S.; Voyiatzis, G.A.; Konstantakopoulou, F.; Kallitsis, J.K., Macromolecules in press 1999.

5. Bower, D. I. J. Polym. Sci. Polym. Phys. Ed. 1972, 10, 2135.

Παράρτημα 1