ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ
ΤΜΗΜΑ ΧΗΜΕΙΑΣ
ΕΠΕΑΕΚ- ΠΜΣ: ΕΦΗΡΜΟΣΜΕΝΗ ΜΟΡΙΑΚΗ ΦΑΣΜΑΤΟΣΚΟΠΙΑ
ΥΠΕΥΘΥΝΟΣ ΕΡΓΟΥ: Σ. Κ. ΦΑΡΑΝΤΟΣ
ΣΤΟΙΧΕΙΑ ΦΑΣΜΑΤΟΣΚΟΠΙΑΣ ΥΠΕΡΥΘΡΟΥ
Ε. Ι. ΚΑΜΙΤΣΟΣ & Γ. Δ. ΧΡΥΣΙΚΟΣ
ΙΝΣΤΙΤΟΥΤΟ ΘΕΩΡΗΤΙΚΗΣ & ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ
ΕΘΝΙΚΟ ΙΔΡΥΜΑ ΕΡΕΥΝΩΝ
ΙΟΥΛΙΟΣ 1999
ΕΠΕΑΕΚ – ΠΜΣ: ΕΦΗΡΜΟΣΜΕΝΗ ΜΟΡΙΑΚΗ ΦΑΣΜΑΤΟΣΚΟΠΙΑ
ΠΕΡΙΕΧΟΜΕΝΑ
|
ΑΣΚΗΣΗ 1 |
Εισαγωγή στην Φασματοσκοπία Υπερύθρου |
3 |
|
ΑΣΚΗΣΗ 2 |
Τεχνικές Ανακλαστικότητας στο Υπέρυθρο |
26 |
|
ΑΣΚΗΣΗ 3 |
Μελέτη Μοριακού Προσανατολισμού με Φασματοσκοπία Πολωμένου Υπερύθρου |
39 |
|
ΑΣΚΗΣΗ 4 |
Εισαγωγή στην Φασματοσκοπία Εγγύς Υπερύθρου |
52 |
|
ΠΑΡΑΡΤΗΜΑ |
Η Φασματοσκοπία Υπερύθρου στο Διαδίκτυο |
65 |
A
ΣΚΗΣΗ 1ΕΙΣΑΓΩΓΗ ΣΤΗ ΦΑΣΜΑΤΟΣΚΟΠΙΑ ΥΠΕΡΥΘΡΟΥ
Σκοπός
Η παρούσα άσκηση αποσκοπεί στην εξοικείωση των φοιτητών με την φασματοσκοπία υπερύθρου (Infrared, IR) και ειδικότερα με την τεχνική μετασχηματισμού Fourier (FT-IR). Η μέτρηση χαρακτηριστικών φασμάτων στο υπέρυθρο θα γίνει με την τεχνική της διαπερατότητας σε δείγματα ελευθέρων πολυμερικών υμενίων και σε διασπορά υλικών σε δισκία KBr. Για την καλύτερη κατανόηση της φασματοσκοπίας υπερύθρου θεωρείται σκόπιμο να προηγηθεί του πειραματικού μέρους η παράθεση βασικών αρχών και εννοιών που διέπουν τη φασματοσκοπία αυτή. Επίσης, παρουσιάζονται περιληπτικά οι αρχές λειτουργίας, οι δυνατότητες και τα πλεονεκτήματα της τεχνικής υπερύθρου με μετασχηματισμό Fourier.
1. ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ
1.1. Εισαγωγικά Στοιχεία
Η συνολική ενέργεια ενός μορίου οφείλεται σε πυρηνικές (E
nucl) και ηλεκτρονιακές (Eelec) συνεισφορές και δίδεται από την σχέση:Etot=Enucl+Eelec
Η ενεργειακή αυτή διάκριση βασίζεται στο γεγονός ότι η ταχύτητα των ηλεκτρονίων είναι πολύ μεγαλύτερη αυτής των πυρήνων. Η E
nucl απαρτίζεται από επί μέρους ενέργειες:Enucl = Etrans + Erot + Evib
όπου E
trans είναι η ενέργεια παραλλήλου μετακινήσεως του μορίου, Erot η ενέργεια περιστροφής και Evib η ενέργεια ταλαντώσεως (δονήσεως). Διευκρινίζεται ότι στην μελέτη των ηλεκτρονιακών διεγέρσεων και εσωτερικών κινήσεων του μορίου δεν ενδιαφέρει η Etrans.Οταν ένα μόριο τίθεται σε ηλεκτρομαγνητικό πεδίο (π.χ. φωτίζεται με ακτινοβολία κατάλληλης συχνότητας) γίνεται μεταφορά ενέργειας από το πεδίο στο μόριο όταν ικανοποιείται η συνθήκη του
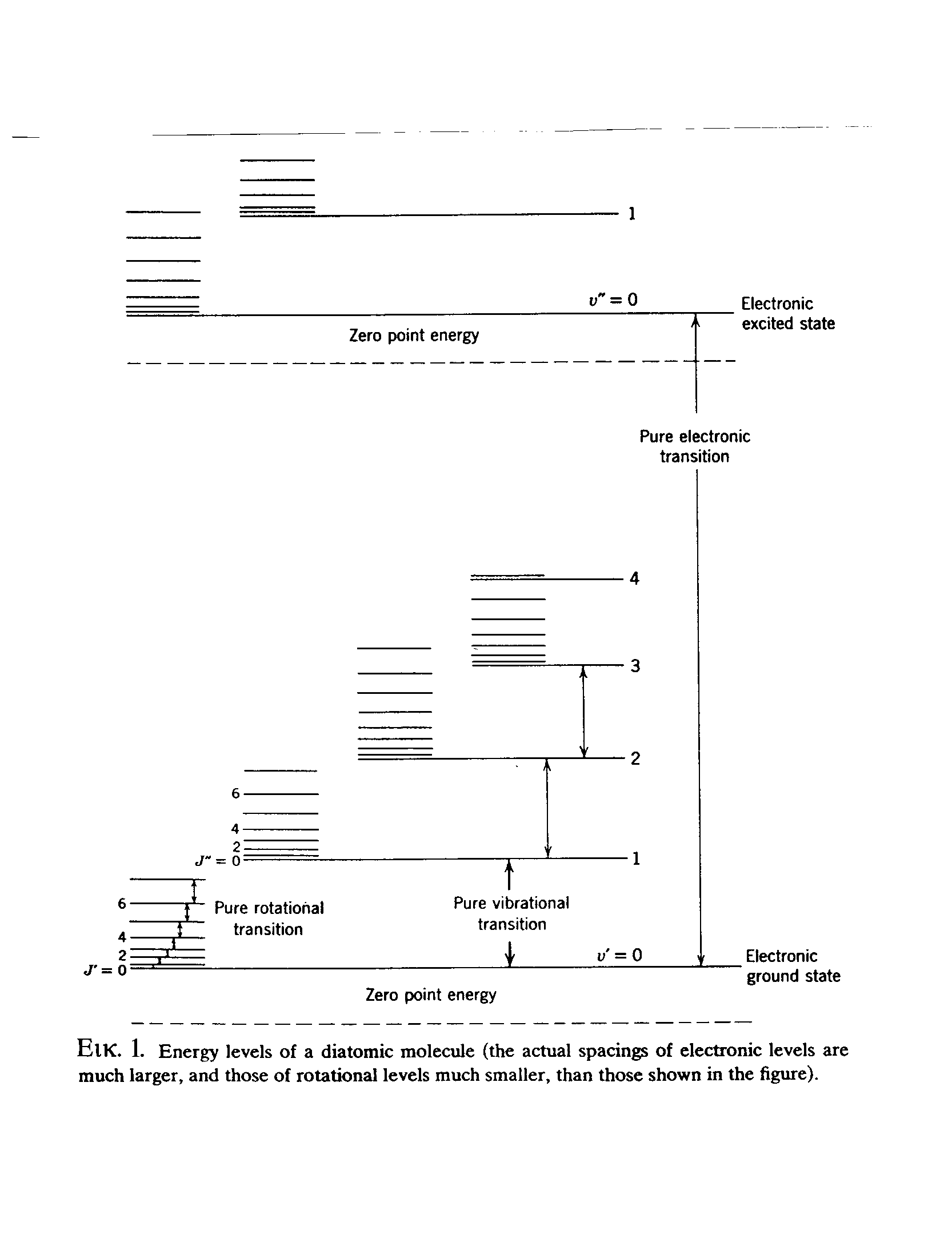
Bohr, ΔΕ=hν, όπου ΔΕ η διαφορά ενέργειας μεταξύ δύο κβαντισμένων ενεργειακών καταστάσεων του μορίου, h η σταθερά του Planck και ν η συχνότητα της ακτινοβολίας. Στην Εικ.1 δίδονται σχηματικά οι ενεργειακές στάθμες ενός διατομικού μορίου. Κάθε ηλεκτρονιακή στάθμη υποδιαιρείται σε στάθμες ταλαντώσεων, οι οποίες χαρακτηρίζονται από τον κβαντικό αριθμό ταλαντώσεως υ, ενώ κάθε στάθμη ταλαντώσεως υποδιαιρείται σε στάθμες περιστροφής των οποίων η ενέργεια χαρακτηρίζεται από τον κβαντικό αριθμό J.
Εικόνα 1.
Σχηματικό ενεργειακό διάγραμμα διατομικού μορίου.
Οι ενεργειακές στάθμες λόγω περιστροφής ευρίσκονται η μία πλησίον της άλλης και επομένως μεταπτώσεις μεταξύ γειτονικών σταθμών λαμβάνουν χώρα σε χαμηλές συχνότητες (ή μεγάλα μήκη κύματος). Τέτοιες μεταπτώσεις δίδουν τα φάσματα περιστροφής (rotational spectra) τα οποία μετρώνται στην περιοχή των μικροκυμάτων και του άπω υπερύθρου, δηλαδή 1cm
-1 (104 μm) έως περίπου 102 cm-1 (102 μm). Υπενθυμίζεται ότι η συχνότητα, ν, μετατρέπεται σε κυματάριθμους, ũ, ή σε μήκος κύματος, λ, μέσω της γνωστής σχέσεως λ=c/ν=1/ũ, όπου c η ταχύτητα του φωτός. Η απόσταση μεταξύ δονητικών ενεργειακών σταθμών είναι μεγαλύτερη, με αποτέλεσμα οι σχετικές ενεργειακές μεταπτώσεις να λαμβάνουν χώρα σε μεγαλύτερες συχνότητες (μικρότερα μήκη κύματος) απ’ ότι οι μεταπτώσεις λόγω περιστροφής. Τα δονητικά φάσματα (vibrational spectra) μετρώνται συνήθως στην περιοχή 102 cm-1 (102 μm) έως 104 cm-1 (1μm) (περιοχή υπερύθρου). Τέλος, η μεγάλη ενεργειακή απόσταση μεταξύ των ηλεκτρονιακών ενεργειακών σταθμών έχει ως αποτέλεσμα τα αντίστοιχα ηλεκτρονιακά φάσματα (electronic spectra) να μετρώνται στην περιοχή 104 cm-1 (1μm) έως 105 cm-1 (0.1 μm) (περιοχή ορατού και υπεριώδους).Τα φάσματα ταλαντώσεως ή δονητικά φάσματα συνήθως μετρώνται πειραματικά ως φάσματα υπερύθρου και φάσματα Raman. Οι δύο αυτοί τύποι των δονητικών φασμάτων έχουν διαφορετική φυσική προέλευση. Ενώ τα φάσματα υπερύθρου προέρχονται από μεταπτώσεις μεταξύ δύο γειτονικών ενεργειακών σταθμών του μορίου λόγω απορρόφησης ή εκπομπής υπερύθρου ακτινοβολίας, τα φάσματα Raman οφείλονται στην σκέδαση ακτινοβολίας (συνήθως ορατού ή υπεριώδους) λόγω ηλεκτρονιακής πόλωσης του μορίου. Ασκήσεις σχετικές με το φαινόμενο Raman θα γίνουν σε εργαστήριο άλλου Ερευνητικού Κέντρου, συνεπώς οι επόμενες ενότητες εστιάζουν στην φασματοσκοπία υπερύθρου.
1.2. Ταλάντωση Διατομικού Μορίου
Υποθέτουμε διατομικό μόριο ΑΒ, με μάζες ατόμων m
1 και m2. Η ταλάντωση του διατομικού μορίου μπορεί να αναχθεί στην κίνηση ενός σώματος μάζης μ, του οποίου η μετατόπιση από την θέση ισορροπίας x ισούται με την μεταβολή της απόστασης των ατόμων, x=r-re, όπου re είναι η απόσταση ισορροπίας. Η μάζα μ ονομάζεται ανηγμένη μάζα και δίδεται από την σχέση:μ=m
1m2/(m1+m2)
ενώ η κινητική ενέργεια του συστήματος είναι:
Τ = (1/2) μ (dx/dt)
2Εάν υποθέσουμε ότι η δύναμη επαναφοράς στην θέση ισορροπίας υπακούει στον νόμο του Hooke,
F(x)= -kx
όπου k είναι η σταθερά δυνάμεως, τότε το δυναμικό V(x) που δημιουργεί η δύναμη προκύπτει από την σχέση:
F(x)=-(dV(x)/dx) Þ V(x)=-ò F(x) dx=(1/2) kx2
Η παραπάνω σχέση δείχνει ότι υπό τις συνθήκες αυτές το σύστημα αποτελεί έναν αρμονικό ταλαντωτή του οποίου η δυναμική ενέργεια δίδεται γραφικά στην Εικ. 2.
Η κβαντομηχανική εξέταση του προβλήματος προϋποθέτει επίλυση της χρονικώς ανεξάρτητης μορφής της εξίσωσης Schrödinger με δυναμικό V(
x),
-(ħ2
/2μ) (d2Ψ/dx2)+V(x) Ψ(x)=E Ψ(x)όπου Ψ(x) είναι οι ιδιοσυναρτήσεις και Ε οι ιδιοτιμές της ενέργειας που προκύπτουν από την παραπάνω διαφορική εξίσωση. Η εξίσωση αυτή γράφεται τελικά υπό την μορφή:
(d2
Ψ/dx2)+(2μ/ħ2)[Ε-(1/2) kx2] Ψ(x)=0
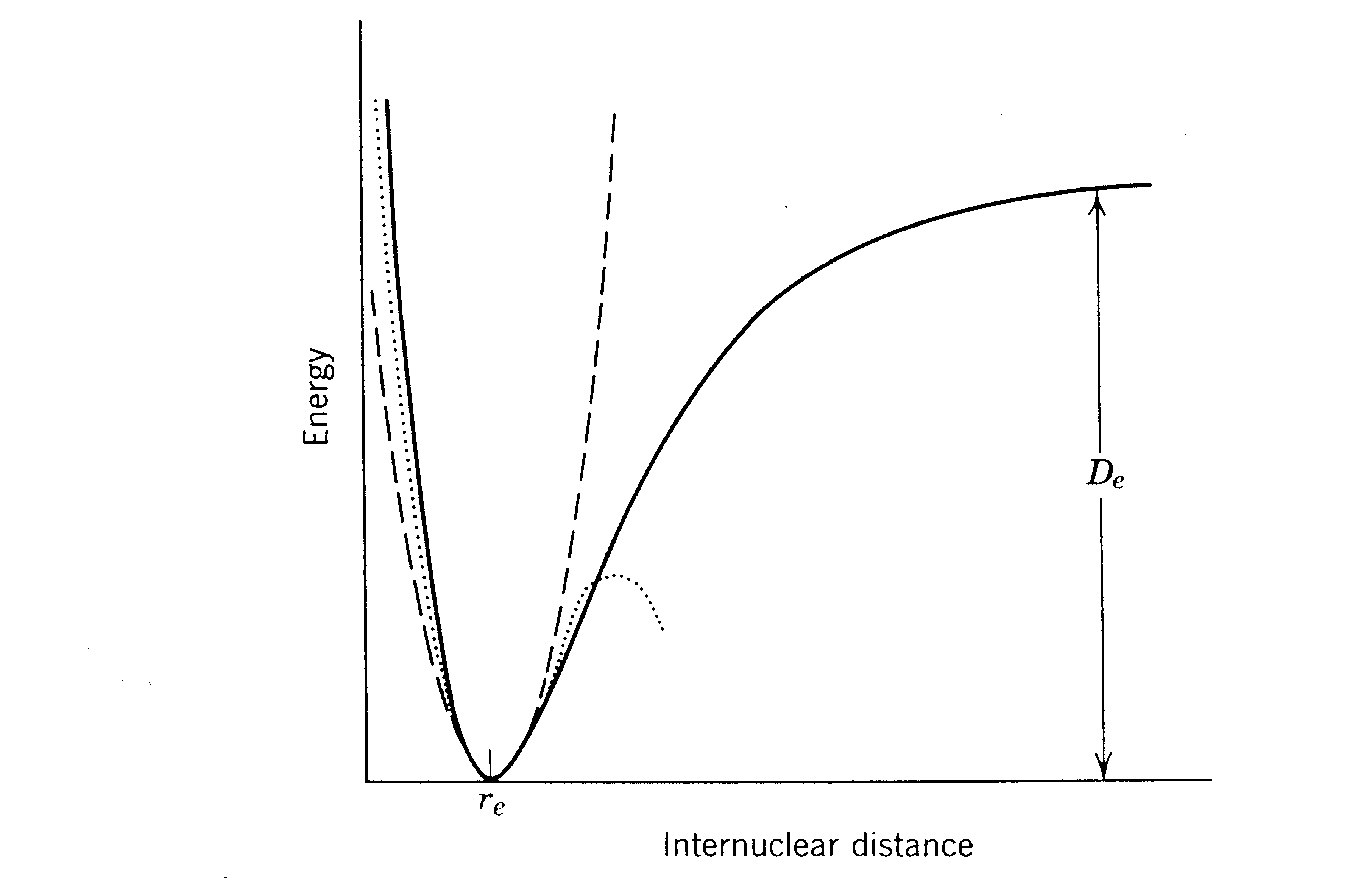
Εικόνα 2. Δυναμική ενέργεια αρμονικού ταλαντωτή (διακεκομμένη γραμμή), αρμονικού ταλαντωτή με κυβικό όρο (εστιγμένη γραμμή) και πραγματικού διατομικού μορίου (συνεχής γραμμή).
και από την επίλυσή της προκύπτει ότι οι ιδιοτιμές της ενέργειας έχουν την μορφή:
Ευ= hν (υ
+1/2)= hcũ (υ+1/2)με συχνότητα δόνησης,
ν=(1/2π) (k/μ)
1/2 ή ũ=(1/2πc) (k/μ)1/2
όπου η συχνότητα ũ δίδεται σε κυματάριθμους (
cm-1) και ο κβαντικός αριθμός δόνησης υ λαμβάνει τις τιμές 0,1,2,3...Οι αντίστοιχες ιδιοσυναρτήσεις λαμβάνουν την μορφή:
Ψυ=[(α/π)
1/4]/(2υ υ!)1/2 exp(-αx2/2) Hυ(α1/2 x)όπου α=2π (μ
k)1/2/h και Hυ(α1/2 x) είναι το πολυώνυμο Hermite βαθμού υ, το οποίο λαμβάνει την γενική μορφή,H
υ(y) = (-1)υ exp(y2) dυexp(-y2)/dyυΣτην περίπτωση μή αρμονικού ταλαντωτού λαμβάνεται και ο δεύτερος όρος στην ανάπτυξη της δύναμης επαναφοράς F(x) σε σειρά Taylor,
F(x)=-kx+ (x2/2) d2F(x)/dx2
οπότε το δυναμικό γίνεται:
V(x) =(1/2) kx2 - (Do/6) x3
όπου
Do=d2F(x)/dx2. Δηλαδή, συμπεριλαμβάνεται ένας κυβικός όρος στο δυναμικό του αρμονικού ταλαντωτού, η δε ενέργεια De=Do+(1/2)hν ονομάζεται ενέργεια διαστάσεως (Εικ. 2). Το νέο δυναμικό οδηγεί σε ιδιοτιμές ενέργειας της μορφής:Ευ=hc ω
e (υ+1/2) - hc xeωe (υ+1/2)2όπου ο όρος x
eωe ονομάζεται σταθερά αναρμονικότητας. Είναι προφανές ότι λόγω αναρμονικότητος οι ενεργειακές στάθμες δεν είναι ισαπέχουσες, σε αντίθεση με την αρμονική ταλάντωση, αλλά πλησιάζουν σταδιακά καθώς ο κβαντικός αριθμός υ αυξάνει.
1.3. Kανόνες Επιλογής
Κλασική θεώρηση
Σύμφωνα με την κλασική ηλεκτρομαγνητική θεωρία ένα παλλόμενο δίπολο εκπέμπει ή απορροφά ακτινοβολία της οποίας η συχνότητα είναι ίση με αυτή της ταλαντώσεώς του. Η ένταση της απορρόφησης ή εκπομπής της ακτινοβολίας είναι ανάλογος του τετραγώνου της μεταβολής της διπολικής του ροπής, μ, ως προς την μεταβολή της απόστασης του διπόλου, x,
Ι µ
(¶ μ/¶ x)2Είναι προφανές ότι μη μηδενική ένταση απορρόφησης ή εκπομπής ακτινοβολίας προϋποθέτει:
(¶
μ/¶ x)¹ 0
Η εξίσωση αυτή αποτελεί τον “κλασικό” κανόνα επιλογής για απορρόφηση/εκπομπή ακτινοβολίας υπερύθρου.
Κβαντομηχανική θεώρηση
Σύμφωνα με την κβαντομηχανική θεωρία, η απορρόφηση ακτινοβολίας οδηγεί σε μετάπτωση από την δονητική κατάσταση που χαρακτηρίζεται από την ιδιοσυνάρτηση Ψκ σε αυτή που χαρακτηρίζεται από την ιδιοσυνάρτηση Ψ
m εφ’ όσον το παρακάτω ολοκλήρωμα (transition mοment) είναι μη μηδενικό,ò
Ψ*m μ Ψκ dr ¹ 0όπου μ είναι ο τελεστής διπολικής ροπής (transition moment operator). Αναπτύσσοντας το μ σε σειρά ως προς x,
μ
= μo+(¶ μ/¶ x)ox+...η προηγούμενη εξίσωση γίνεται,
ò
Ψ*m μ Ψκ dr = ò Ψ*m [μo+(¶ μ/¶ x)ox] Ψκ dr = μo ò Ψ*m Ψκ dr +(¶
μ/¶ x)oò Ψ*m x Ψκ dr = (¶ μ/¶ x)oò Ψ*m x Ψκ dr ¹ 0Το παραπάνω ολοκλήρωμα είναι μή μηδενικό εφ’ όσον,
(¶
μ/¶ x)ο¹ 0 και m=k± 1 δηλ. Δυ=± 1Συνεπώς,
Τονίζεται ότι στην περίπτωση μή αρμονικού ταλαντωτού (όπως είναι η πλειοψηφία των μορίων) γίνεται δυνατή η μετάπτωση και μεταξύ μή γειτονικών δονητικών καταστάσεων, γεγονός που οδηγεί στην εμφάνιση υπέρτονων ταινιών (overtones) με συχνότητα nνο, όπου n=1,2,3.. και ταινιών εκ συνδυασμού με συχνότητα nν1± ν2 (combination bands).
Σε σύγκριση με την φασματοσκοπία υπερύθρου αναφέρουμε ότι οι κανόνες επιλογής για την φασματοσκοπία Raman είναι,
(¶
α/¶ x)ο¹ 0 και Δυ=± 1όπου α είναι η πολωσιμότητα (polarizability) του μορίου.
1.4. Κανονικοί Τρόποι Δόνησης Μορίου
Ενα μόριο που αποτελείται από Ν άτομα έχει 3Ν βαθμούς ελευθερίας, εκ των οποίων οι τρείς περιγράφουν την μετατόπιση του κέντρου βάρους του και άλλοι τρεις την περιστροφή του γύρω από τους τρεις καρτεσιανούς άξονες. Συνεπώς, 3Ν-6 βαθμοί ελευθερίας περιγράφουν τις ταλαντώσεις (δονήσεις) του μορίου. Στην περίπτωση γραμμικών μορίων αρκούν δύο βαθμοί ελευθερίας για την περιγραφή της περιστροφής και επομένως οι δονητικοί βαθμοί ελευθερίας γίνονται 3Ν-5. Οι βασικοί αυτοί τρόποι δόνησης του μορίου (3Ν-6, ή 3Ν-5) ονομάζονται κανονικοί τρόποι δόνησης (normal vibrations, ή normal vibrational modes), δεδομένου ότι οποιαδήποτε δόνηση του μορίου μπορεί να περιγραφεί ως γραμμικός συνδυασμός
των κανονικών τρόπων δονήσεως.Στην Εικ.3 δίδονται ως παράδειγμα οι κανονικές δονήσεις δύο τριατομικών μορίων, ενός γραμμικού (CΟ
2) και ενός μη γραμμικού (Η2Ο). Η δόνηση του CO2 με συχνότητα ν2 είναι διπλά εκφυλισμένη, δηλ. ν2a=ν2b. Είναι προφανές ότι η δόνηση συχνότητος ν1 δεν μεταβάλλει την διπολική ροπή του CO2 και συνεπώς είναι ανενεργή στο υπέρυθρο, αλλά ενεργή στο Raman. Αντίθετα, οι δονήσεις του CO2 ν2 και ν3 είναι ενεργές στο υπέρυθρο και ανενεργές στο Raman. Γενικώς, σε μόρια με κέντρο συμμετρίας οι δονήσεις που είναι ενεργές στο IR δεν είναι ενεργές στο Raman, και αντίστροφα. Στο μή γραμμικό Η2Ο και οι τρεις δονήσεις είναι ενεργές στο IR και Raman ταυτόχρονα.
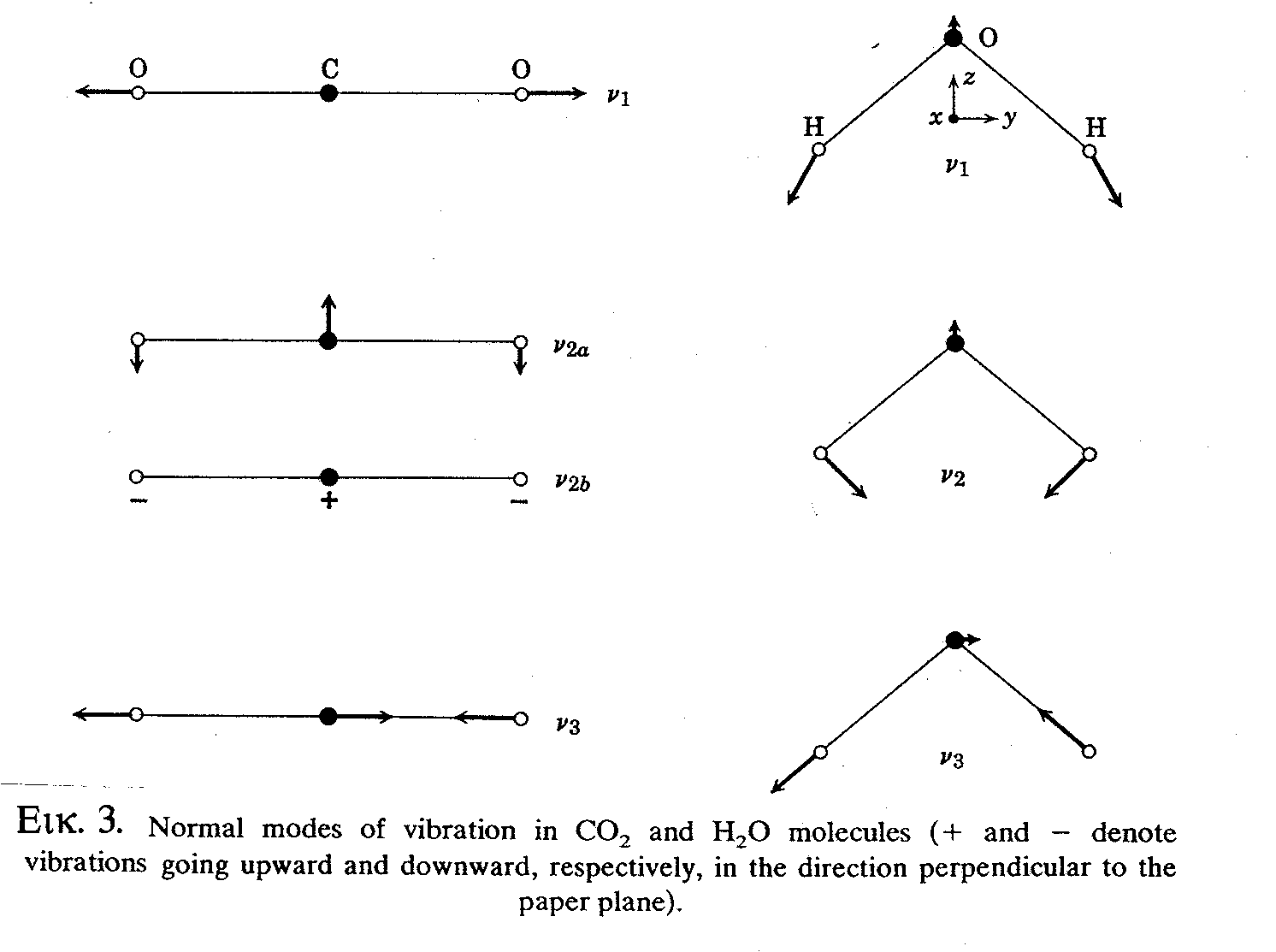
Εικόνα 3.
Κανονικοί τρόποι δόνησης γραμμικού (CΟ2) και κεκαμμένου (Η2Ο) τριατομικού μορίου.
Στην Εικ.4 δίδονται οι κανονικές δονήσεις ενός τετραεδρικού συστήματος, ΧΥ
4 (π.χ. το ιόν SO42-). Τονίζεται ότι η τελείως συμμετρική δόνηση έκτασης του δεσμού Χ-Υ (συχν. ν1) είναι ενεργή μόνο στο Raman, όπως και η δόνηση κάμψεως με συχνότητα ν2. Αντίθετα, η ασύμμετρη δόνηση έκτασης του Χ-Υ δεσμού (συχν. ν3) και η δόνηση κάμψης (συχν. ν4) είναι ενεργές ταυτόχρονα στο υπέρυθρο και στο Raman.
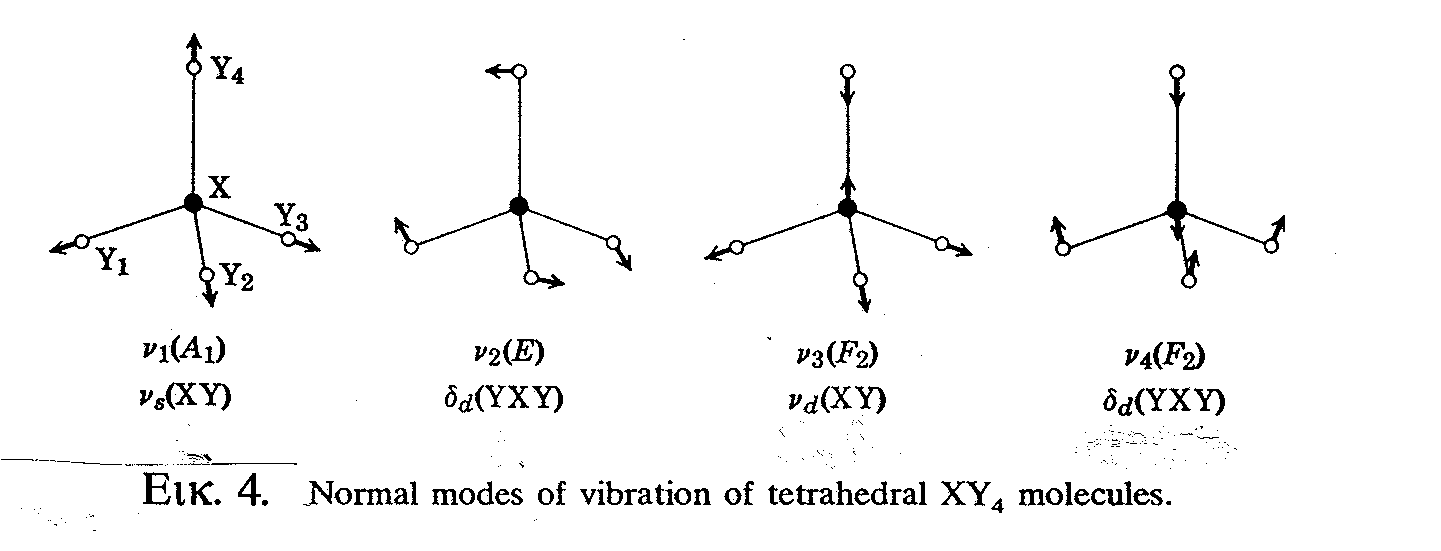
Εικόνα 4. Κανονικοί τρόποι δόνησης τετραεδρικού μορίου/ιόντος.
Kαθώς αυξάνει ο αριθμός ατόμων ενός μορίου, ιόντος, ή ατομικού συγκροτήματος γενικότερα, αυξάνει και η πολυπλοκότητα των κανονικών δονήσεων. Τούτο φαίνεται χαρακτηριστικά στην Εικ.5 στην οποία δίδονται οι κανονικές δονήσεις της μεθυλενομάδας (CH
2).
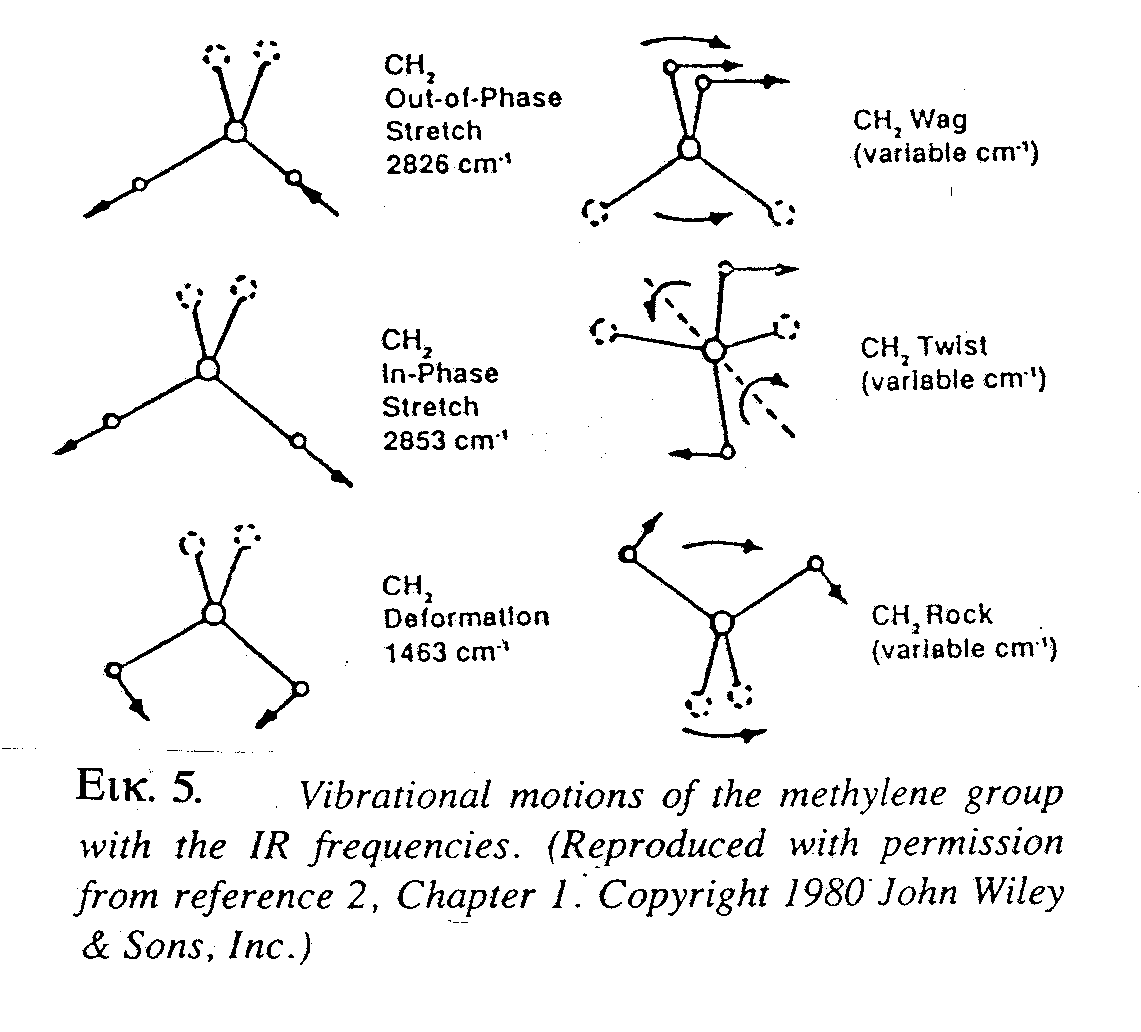
Εικόνα 5
. Κανονικοί τρόποι δόνησης της μεθυλενομάδας (CH2).
Η συμμετρία των κανονικών δονήσεων ενός μορίου, καθώς και η ενεργότητά τους στο IR/Raman, μπορεί να ευρεθεί με εφαρμογή της θεωρίας ομάδων, η οποία αποτελεί ιδιαίτερο κεφάλαιο της δονητικής φασματοσκοπίας.
2. ΦΑΣΜΑΤΟΣΚΟΠΙΑ ΥΠΕΡΥΘΡΟΥ ΜΕ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟ
FOURIER (FT-IR)
2.1. Στοιχεία Θεωρίας
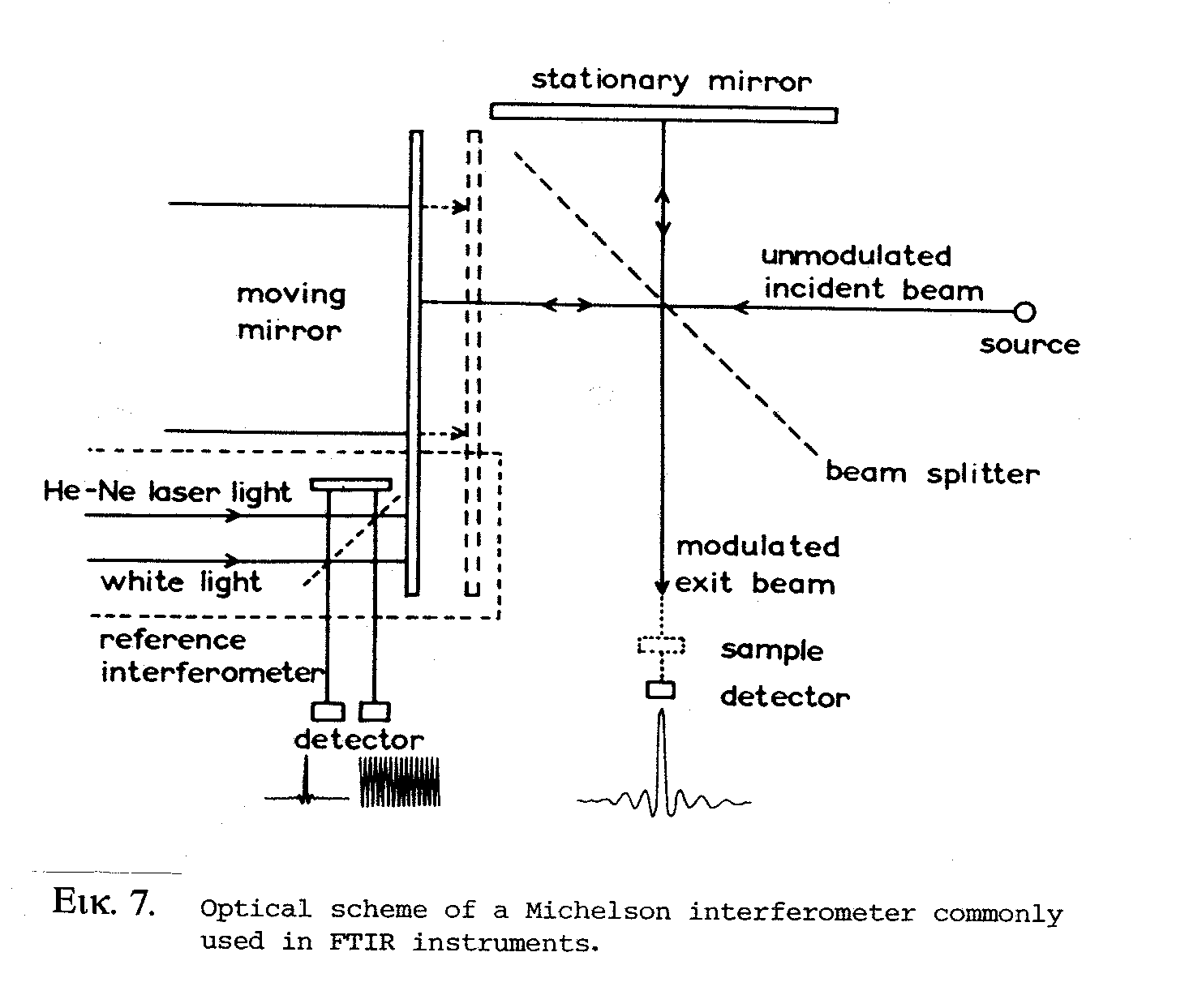
Η περιοχή εφαρμογών της φασματοσκοπίας υπερύθρου έχει επεκταθεί σημαντικότατα τις τελευταίες δεκαετίες λόγω της ανάπτυξης της φασματοσκοπίας υπερύθρου με μετασχηματισμό Fourier. Τούτο οφείλεται κατά κύριο λόγο στην θεαματική ανάπτυξη των υπολογιστών και στην βαθμιαία χρήση τους και σε θέματα φασματοσκοπίας. Στην συνήθη φασματοσκοπία υπερύθρου (dispersive IR spectroscopy) η πολυχρωματική ακτινοβολία της πηγής αναλύεται με χρήση μονοχρωμάτωρα (πρίσμα ή φράγμα) και ανιχνεύεται κατά συχνότητες ν+Δν, όπου το Δν καθορίζεται από το εύρος των σχισμών του φωτομέτρου. Αντίθετα, στην φασματοσκοπία υπερύθρου με μετασχηματισμό Fourier (FT-ΙR) το συμβολόμετρο Michelson, γνωστό ήδη από τα τέλη του περασμένου αιώνα, αποτελεί την καρδιά της τεχνικής. Το συμβολόμετρο Michelson απαρτίζεται από δύο κάτοπτρα κάθετα μεταξύ τους, εκ των οποίων το ένα είναι κινητό, και ένα διαιρέτη δέσμης (beam splitter) που παρεμβάλλεται μεταξύ των σε γωνία 45ο (Εικ.6).
Για την κατανόηση της λειτουργίας του συμβολομέτρου ας θεωρήσουμε την απλούστερη περίπτωση κατά την οποία η ακτινοβολία μιάς μονοχρωματικής πηγής συχνότητας νο ( όπου νο ο κυματάριθμος της ακτινοβολίας, δηλ. νο=1/λο) χωρίζεται στον διαιρέτη δέσμης σε δύο δέσμες ίσης εντάσεως Ι(νο). Οταν μετά την ανάκλαση στους δύο καθρέπτες οι δύο δέσμες συναντώνται εκ νέου στον διαιρέτη δέσμης συμβάλλουν καί δίδουν συνολική ένταση:
Ι(φ) = 2 Ι(νο) (1+cosφ)
Η ακτινοβολία έντασης Ι(φ) κατευθύνεται στο δείγμα και στη συνέχεια στον ανιχνευτή. Η διαφορά φάσης φ μπορεί να εκφραστεί σαν συνάρτηση της διαφοράς των δύο οπτικών διαδρομών, s, και του μήκους κύματος λο της ακτινοβολίας,
φ
= 2π (s/λο)Συνεπώς, η ένταση της ακτινοβολίας μετά την συμβολή γίνεται,
Ι
(s)= 2 Ι(νο) (1+cos2πνοs)Είναι προφανές ότι παρατηρείται ενισχυτική συμβολή (constructive interference) όταν
s = n
λο, n= 0, ± 1, ± 2…Αντίθετα, παρατηρείται μηδενική ένταση όταν,
s = (n+1/2) λο
Στην πραγματικότητα όμως η πηγή εκπέμπει ένα συνεχές φάσμα συχνοτήτων ν και επομένως η ένταση της ακτινοβολίας γίνεται:
I(s)= 2 ![]()
Ι8
+ 2Συνεπώς, η ένταση I(s) αποτελείται από ένα σταθερό μέρος, I8 , και ένα μεταβαλλόμενο: 2
F(s) = 2 ![]()
Στην Εικ.7 φαίνονται τα φάσματα εκπομπής και τα συμβολογράμματα μιάς μονοχρωματικής και μιάς πολυχρωματικής πηγής. Τα συμβολογράμματα είναι συμμετρικά ως προς s=0 και η μέγιστη ένταση για την πολυχρωματική πηγή λαμβάνεται για s=0.
Από την μετρούμενη συνάρτηση F(s), δηλ. ένταση ακτινοβολίας σαν συνάρτηση της μετατόπισης του κινητού κατόπτρου, προκύπτει εύκολα το φάσμα υπερύθρου Ι(ν), μέσω του μετασχηματισμού Fourier, εκ του οποίου προέρχεται και η ονομασία
Fourier transform spectroscopy,I(ν) = ![]() F(s) cos2πνs ds = 2
F(s) cos2πνs ds = 2 ![]() F(s) cos2πνs ds
F(s) cos2πνs ds
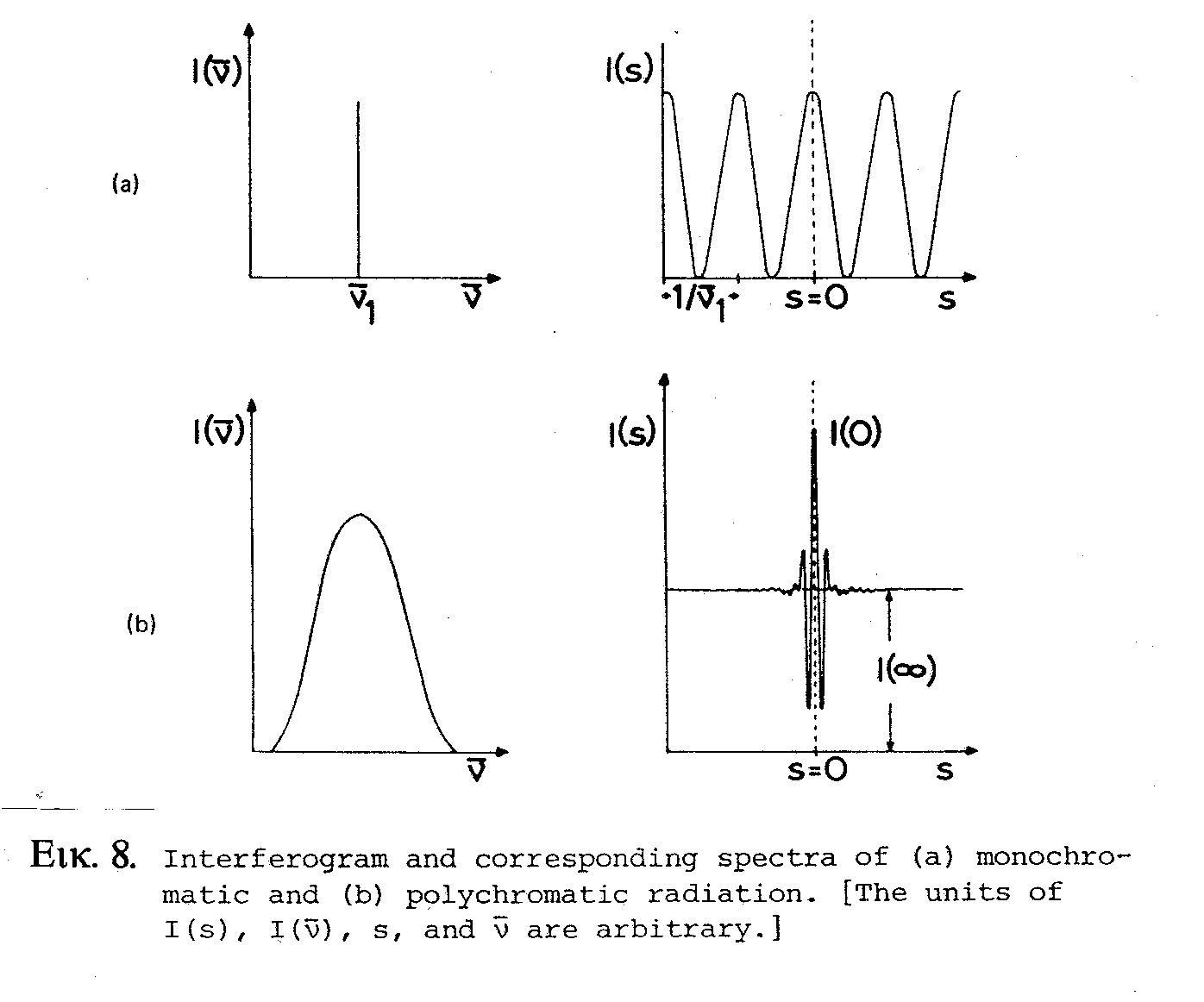
Εικόνα 7. Συμβολογράμματα [
I(s)] και αντίστοιχα φάσματα εκπομπής [I(ν)] μονοχρωματικής (a) και πολυχρωματικής (b) πηγής.
Σύμφωνα με την παραπάνω εξίσωση, ο υπολογισμός του φάσματος Ι(ν) προϋποθέτει την γνώση του συμβολογράμματος για διαφορές οπτικών διαδρομών 0=
s= 8 . Στην πράξη τούτο δεν είναι δυνατόν, δεδομένου ότι το s λαμβάνει τιμές μεταξύ 0 και smax. Μαθηματικά, τούτο αντιστοιχεί με πολλαπλασιασμό του F(s) με μιά συνάρτηση Dr(s) (instrumental line shape) η οποία μηδενίζει την ένταση για ορισμένες τιμές του s. Η διαδικασία αυτή λέγεται αποδισμός (apodization) και αντιστοιχεί στην γνωστή συνάρτηση σχισμής (slit function) σε dispersive φωτόμετρο. Παράδειγμα συνάρτησης Dr(s) είναι η συνάρτηση boxcar,Dr(s) =1
όταν - smax< s< +smaxDr(s) =0
όταν s< -smax, s> +smaxΑν D
r(ν) είναι η Fourier transform της Dr(s) τότε το προκύπτον φάσμα είναι:Ι
(ν).Dr(ν) =όπου Ι(ν) είναι το πραγματικό φάσμα. Η φυσική σημασία του Ι(ν).D
r(v) είναι ότι το φάσμα έχει καθορισμένο εύρος το οποίο ισούται με Δν=1/2smax για τετραγωνικό αποδισμό και Δν=1/smax για τριγωνικό αποδισμό. Επίσης, η διακριτική ικανότητα του οργάνου είναι R=2νsmax για τετραγωνικό αποδισμό και R=νsmax για τριγωνικό αποδισμό.Οπως παρατηρείται στην Εικ. 6 το κινητό κάτοπτρο του συμβολομέτρου Michelson αποτελεί επίσης μέρος ενός μικροτέρου συμβολομέτρου (συμβολόμετρο αναφοράς) όπου οι φωτεινές πηγές είναι ένα μικρό laser He-Ne και μιά πηγή λευκού φωτός. Το laser He-Ne χρησιμοποιείται για την μέτρηση της μετατόπισης του κινητού κατόπτρου με μεγάλη ακρίβεια, και συνεπώς της συχνότητος της ακτινοβολίας, δεδομένου ότι η ν(He-Ne)=15802,4117 cm
-1. Το συμβολογράφημα του λευκού φωτός χρησιμοποιείται για να καθορίζει την έναρξη της διαδικασίας συλλογής δεδομένων (trigger). Το σταθερό κάτοπτρο του συμβολομέτρου αναφοράς ρυθμίζεται έτσι ώστε το μέγιστο του συμβολογράμματος του λευκού φωτός να εκδηλώνεται όταν s® smax για το κυρίως συμβολόμετρο.
2.2. Δυνατότητες και Πλεονεκτήματα της Φασματοσκοπίας FT-IR
Kατά την διάρκεια των τελευταίων δύο δεκαετιών έχουν αναπτυχθεί διάφοροι τύποι φασματοφωτομέτρων FTIR, τα οποία παρουσιάζουν διαφορές ως προς το είδος του συμβολομέτρου Michelson που χρησιμοποιούν, το είδος του διαχωριστού δέσμης, την σχεδίαση της οπτικής διαδρομής, το είδος των ανιχνευτών κ.λπ. Τα πλεονεκτήματα/μειονεκτήματα των διαφόρων φωτομέτρων δίδονται αναλυτικά στην εξειδικευμένη βιβλιογραφία (δες για πράδειγμα, P.R. Griffiths, J.A. de Haseth,
Fourier Transform Infrared Spectrometry, Wiley-Interscience, Vol. 83, New York, 1986).H χρήση των υπολογιστών στην φασματοσκοπία FTIR προσφέρει την δυνατότητα ταχείας λήψης πολλαπλών φασμάτων, υπολογισμού του μέσου όρου τους, επεξεργασίας και αποθήκευσης των δεδομένων. Τούτο συνεπώς οδηγεί στην μέτρηση φασμάτων υψηλής ποιότητας. Είναι δυνατή επίσης η αφαίρεση φασμάτων (difference spectroscopy) και επομένως η ακριβής ανίχνευση πολύ μικρών μεταβολών που οφείλονται τόσο στην μεταβαλλόμενη σύσταση, όσο και στην φυσική κατάσταση του δείγματος.
Η ύπαρξη “βιβλιοθήκης” φασμάτων υπερύθρου παρέχει την δυνατότητα ανάλυσης του φάσματος ενός μείγματος συστατικών σε αυτά των επί μέρους συστατικών και επομένως την δυνατότητα ποσοτικής ανάλυσης του μείγματος. Τέλος, είναι δυνατή η μελέτη μοριακών αλλαγών και αλληλεπιδράσεων. Για παράδειγμα, δεσμοί υδρογόνου και ενδομοριακές αλληλεπιδράσεις προκαλούν συνήθως είτε μετατοπίσεις στην συχνότητα απορρόφησης, είτε αλλαγή στο συντελεστή μοριακής απορρόφησης. Και οι δύο αυτές φασματικές διαφορές μπορούν να μελετηθούν λεπτομερώς με την τεχνική των φασμάτων διαφοράς.
Η μεγάλη ευαισθησία που χαρακτηρίζει την φασματοσκοπία FTIR μετατρέπεται σε μειονέκτημα στην περίπτωση που η ατμόσφαιρα του φωτομέτρου δεν έχει πλήρως εκκενωθεί, ή αντικατασταθεί με άζωτο. Τότε, το φάσμα υπερύθρου παρουσιάζει έντονες απορροφήσεις που οφείλονται στο Η
2Ο και το CO2 του χώρου του φωτομέτρου. Το σοβαρότερο όμως μειονέκτημα της φασματοσκοπίας FTIR είναι η απαιτούμενη ακριβής ρύθμιση των οπτικών του οργάνου, κυρίως του συμβολομέτρου Michelson. Σε αντίθεση με τα συμβατικά φασματοφωτόμετρα, που δίνουν κακής ποιότητας αλλά χρησιμοποιήσιμα φάσματα όταν δεν είναι καλώς ρυθμισμένα, τα φωτόμετρα FTIR δεν παρέχουν καμμία πληροφορία όταν δεν έχουν καλή ρύθμιση.
ΒΙΒΛΙΟΓΡΑΦΙΑ
1. C.T.H. Schutte, The Theory of Molecular Spectroscopy, Vol. I: The Quantum Mechanics and Group Theory of Vibrating and Rotating Molecules, North Holland, Amsterdam, 1976.
2. K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Wiley, New York, 1978.
3. P.G. Griffiths and J.A. de Haseth, Fourier Transform Infrared Spectroscopy, Wiley, New York, 1986.
4. A.Τσατσά, Σημειώσεις Ανοργάνου Χημείας, Παν/μιο Αθηνών, 1987.
5. J.R. Ferraro and L.J. Basile, Fourier Transform Infrared Spectroscopy, Academic Press, 1985.
6. H.W. Siesler and K. Holland-Moritz, Infrared and Raman Spectroscopy of Polymers, Marcel Dekker, New York, 1980.
7. J.L. Koenig, Spectroscopy of Polymers, ACS, Washington, DC, 1992.
3. ΠΕΙΡΑΜΑΤΙΚΟ ΜΕΡΟΣ
Η παρούσα άσκηση στοχεύει στην εισαγωγή των φοιτητών στην φασματοσκοπία υπερύθρου με μετασχηματισμό Fourier. Στο πρώτο μέρος θα παρακολουθήσουμε τα διαδοχικά στάδια συλλογής δεδομένων και υπολογισμού του φάσματος υπερύθρου με την τεχνική της διαπερατότητας. Ως δείγμα θα χρησιμοποιηθεί λεπτό υμένιο πολυμερούς που είναι πλήρως διαπερατό από την ακτινοβολία υπερύθρου. Το δεύτερο μέρος της άσκησης αποσκοπεί στην εξοικείωση με την διαδικασία παρασκευής κατάλληλων δισκίων
KBr που περιέχουν σε διασπορά υλικά που απορροφούν έντονα στο υπέρυθρο. Στο τρίτο μέρος θα μετρηθούν φάσματα υπερύθρου υμενίων πολυμερούς με διαφορετικό πάχος και θα χρησιμοποιηθούν τα φασματοσκοπικά δεδομένα για τον υπολογισμό του πάχους των υμενίων.Α. Στάδια Συλλογής Δεδομένων και Υπολογισμού του Φάσματος Υπερύθρου
Τα συνήθη φασματοφωτόμετρα υπερύθρου λειτουργούν ως φωτόμετρα απλής δέσμης (single-beam) και συνεπώς μετρώνται χωριστά τα συμβολογράμματα F(s) (δες ενότητα 2.1) της αναφοράς (background) και του δείγματος (sample). Ως αναφορά θεωρείται η οπτική διαδρομή του φωτομέτρου πριν την τοποθέτηση του δείγματος.
Στο Σχήμα Α1 παρουσιάζεται τυπικό συμβολόγραμμα αναφοράς μετρημένο στο φωτόμετρο I
FS 113v της Bruker. Στην συνέχεια τοποθετείται το υπό μελέτη δείγμα σε υποδoχέα, παρεμβάλλεται σε κατάλληλο σημείο της οπτικής διαδρομής και επαναλαμβάνεται η μέτρηση του συμβολογράμματος. Στην άσκηση αυτή ως δείγμα χρησιμοποιείται λεπτή πολυμερική μεμβράνη ευρείας οικιακής χρήσεως (Sanitas Wrap). Το συμβολόγραμμα της μεμβράνης δίδεται επίσης στο Σχήμα 1, όπου παρατηρείται ελάττωση της έντασης και τροποποίηση του αρχικού συμβολογράμματος.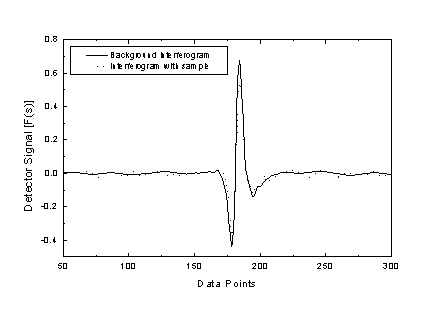
Σχήμα Α1. Συμβολογράμματα αναφοράς (background) και δείγματος (
sample).Στη συνέχεια υπολογίζονται τα φάσματα, I(ν), δηλαδή η ένταση της ακτινοβολίας υπερύθρου ως προς την συχνότητα, με μετασχηματισμό Fourier των συμβολογραμμάτων F(s). Τα φάσματα Ι(ν) της αναφοράς και του δείγματος (
Sanitas Wrap) δίδονται στο Σχήμα Α2. Είναι προφανές ότι το φάσμα Ι(ν) της αναφοράς παριστά το φάσμα εκπομπής της πηγής υπερύθρου, ενώ το φάσμα Ι(ν) του δείγματος δίδει το τροποποιημένο φάσμα εκπομπής της πηγής λόγω επιλεκτικής απορρόφησης ορισμένων συχνοτήτων από το δείγμα.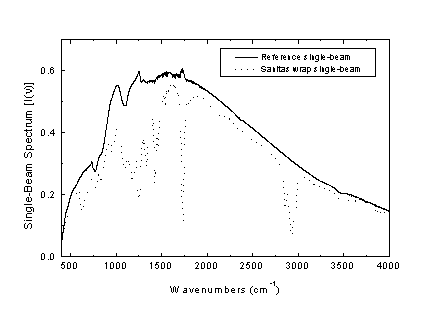
Σχήμα Α2.
Φάσματα υπερύθρου απλής δέσμης: οπτική διαδρομή χωρίς δείγμα (συνεχής γραμμή) και με δείγμα (εστιγμένη γραμμή).
Τέλος, υπολογίζεται το φάσμα διαπερατότητας Τ (transmittance) του δείγματος, ως ο λόγος Τ=[Ι(ν)sample]/[I(v)background]. Το φάσμα απορρόφησης Α (absorbance) υπολογίζεται από την σχέση Α=-logT. Στο Σχήμα Α3 δίδονται τα φάσματα διαπερατότητας και απορρόφησης στο υπέρυθρο της μεμβράνης
Sanitas Wrap. Διευκρινίζεται ότι η χημική σύσταση της εμπορικής αυτής μεμβράνης δεν είναι γνωστή. Η παρουσία όμως της έντονης ταινίας των 1730 cm-1 (δόνηση έκτασης του δεσμού C=O) υποδηλώνει την εστερική φύση της μεμβράνης.
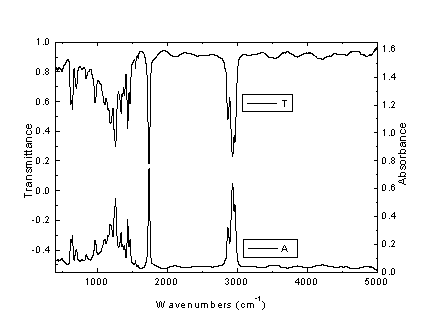
Σχήμα Α3. Φάσματα διαπερατότητας (Τ) και απορρόφησης (Α) στο υπέρυθρο της εμπορικής μεμβράνης
Sanitas Wrap.
Β. Mέτρηση Φασμάτων Υπερύθρου με την Τεχνική Διασποράς σε KBr
Η τεχνική που εφαρμόζεται για την μέτρηση του φάσματος υπερύθρου ενός υλικού εξαρτάται από την φυσική κατάσταση του δείγματος, η οποία και καθορίζει τον τρόπο αλληλεπίδρασης της δέσμης υπερύθρου με το δείγμα. Η πλέον διαδεδομένη και εύχρηστη τεχνική είναι η τεχνική της διαπερατότητας η οποία χρησιμοποιείται όταν το δείγμα μπορεί να παρασκευαστεί υπό μορφή λεπτού φίλμ (π.χ. πολυμερή υλικά), ή να διασπαρεί υπό μορφή κόνεως σε ένα αδρανές μέσο. Στην φασματική περιοχή του μέσου υπερύθρου (400
cm-1 έως 5,000 cm-1) κατάλληλα υλικά διασποράς είναι τα αλογονούχα άλατα των αλκαλίων (π.χ. KBr, NaCl, CsI), τα οποία δεν απορροφούν στην περιοχή αυτή, είναι σχετικά αδρανή και παρουσιάζουν μικρή υγροσκοπικότητα.Εάν Ιο είναι η ένταση της προσπίπτουσας ακτινοβολίας στο δείγμα και Ι η ένταση της ακτινοβολίας που εξέρχεται από το δείγμα, τότε η διαπερατότητα T του δείγματος υπολογίζεται από την σχέση:
Τ=Ι/Ιο
=exp[-α(ν) t]όπου α(ν) είναι ο συντελεστής απορρόφησης του υλικού σε συχνότητα ν και
t το πάχος του δείγματος. Δεδομένου ότι η απορρόφηση A ορίζεται ως A=-logT προκύπτει ότιΑ=α(ν)
t/2.303Η μέτρηση της απορρόφησης επιτρέπει την χρήση της φασματοσκοπίας διαπερατότητας στο υπέρυθρο για ποσοτικές μετρήσεις, λόγω ισχύος του γνωστού νόμου Lambert-Beer,
A = ε(ν) t c
όπου c η συγκέντρωση του υλικού, t το πάχος του δείγματος και ε(ν) ο συντελεστής μοριακής απορροφητικότητας του υλικού σε συχνότητα ν. Από τον συνδυασμό των παραπάνω σχέσεων προκύπτει ότι ο συντελεστής απορρόφησης συνδέεται με τον συντελεστή μοριακής απορροφητικότητας μέσω της σχεσης: α(ν)=2.303ε(ν)c. Οπως θα δούμε αναλυτικά στην δεύτερη άσκηση, ο συντελεστής απορρόφησης ενός υλικού μπορεί να υπολογιστεί με ακρίβεια από την μέτρηση και ανάλυση του φάσματος κατοπτρικής ανακλαστικότητας του υλικού.
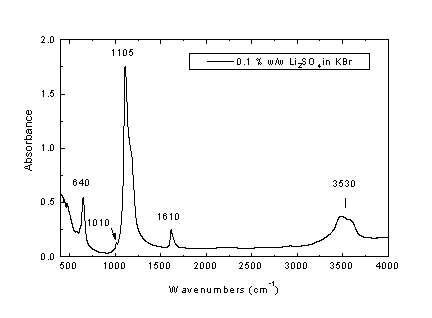
Σχήμα Β1. Φάσμα απορρόφησης του
Li2SO4 στο μέσο υπέρυθρο (δισκίο KBr)Στο Σχήμα Β1 παρουσιάζεται το φάσμα απορρόφησης του
Li2SO4 υπό μορφή διασποράς σε δισκίο KBr. Το φάσμα χαρακτηρίζεται από την παρουσία της ισχυρής ταινίας των 1105 cm-1 η οποία αποδίδεται στην ασύμμετρη δόνηση έκτασης του θειϊκού ιόντος, ν3(SO42-) (δες κανονικούς τρόπους δόνησης τετραεδρικού μορίου/ιόντος στην Εικ. 4, ενότητα 1. 4). Η έντονη ασυμμετρία που παρουσιάζει η ταινία των 1105 cm-1 οφείλεται στο γεγονός ότι η δόνηση ν3(SO42-) είναι τριπλά εκφυλισμένη. Η ταινία των 640 cm-1 προέρχεται από την ενεργή στο υπέρυθρο δόνηση κάμψης του θειϊκού ιόντος, ν4(SO42-). Διευκρινίζεται ότι η δεύτερη δόνηση κάμψης, ν2(SO42-), είναι ενεργή στο Raman (465 cm-1), όπως και η όλο συμμετρική δόνησης έκτασης του ιόντος, ν1(SO42-), η οποία αναμένεται να δώσει ισχυρή ταινία Raman περί τους 1010 cm-1. Προσεκτική παρατήρηση του Σχήματος Β1 δείχνει την παρουσία ασθενούς ώμου περί τους 1010 cm-1, γεγονός που υποδηλώνει την ασθενή ενεργοποίηση της δόνησης ν1 στο υπέρυθρο. Τούτο προκύπτει συνήθως λόγω μικρής παραμόρφωσης του τετραέδρου στην στερεά κατάσταση, ως συνέπεια της οποίας επέρχεται η υποβάθμιση της συμμετρίας του ιόντος από Td πιθανώς σε C3v. Η αλλαγή ενεργότητας των κανονικών τρόπων δόνησης ενός τετραέδρου με βαθμιαία υποβάθμιση της συμμετρίας του σε C3v και C2v δίδεται στον παρακάτω πίνακα.Πίνακας 1
. Πίνακας συσχετισμού των ομάδων σημείου Td, C3v και C2v|
Mode |
Td |
C3v |
C2v |
|
Ν 1 |
A1(R) |
A1(R, IR) |
A1(R, IR) |
|
Ν 2 |
E(R) |
E(R, IR) |
A1(R, IR)+A2(R) |
|
ν 3, ν4 |
T2(R, IR) |
A1(R, IR)+E(R, IR) |
A1(R, IR)+B1(R, IR)+B2(R, IR) |
Σημείωση:
R και IR υποδηλώνουν ενεργότητα στο Raman και στο υπέρυθρο, αντίστοιχα.Εκτός από τις ταινίες που οφείλονται σε χαρακτηριστικές δονήσεις του ιόντος
SO42- το Σχήμα Β1 παρουσιάζει και απορροφήσεις στους 1610 cm-1 και στους περίπου 3530 cm-1. Οι ταινίες αυτές οφείλονται στο γεγονός ότι το βρωμιούχο κάλιο δεν είχε ξηρανθεί τελείως και συνεπώς παρουσιάζει και τις ενεργές στο υπέρυθρο δονήσεις του νερού, δηλαδή την δόνηση κάμψης (ν2, 1610 cm-1) και τις δονήσεις έκτασης του δεσμού Ο-Η (ν1 και ν3, περίπου 3530 cm-1), δες Εικ. 3 της ενότητας 1.4.Το Σχήμα Β2 παρουσιάζει το φάσμα απορρόφησης του πολυαιθυλενίου υπό μορφή διασποράς κόνεως σε δισκίο
KBr. Το φάσμα χαρακτηρίζεται από την παρουσία των παρακάτω ισχυρών ταινιών:σε συμφωνία με βιβλιογραφικά δεδομένα.
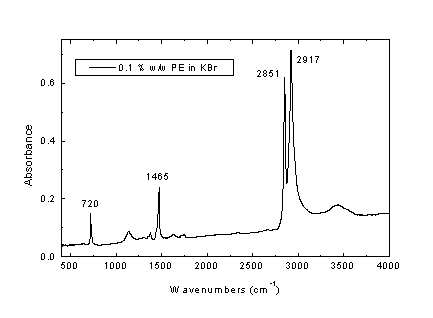
Σχήμα Β2.
Φάσμα απορρόφησης κόνεως πολυαιθυλενίου (PE) στο μέσο υπέρυθρο (δισκίο KBr)
Από τα φάσματα που θα μετρηθούν στην παρούσα άσκηση θα υπολογιστούν οι συντελεστές απορρόφησης α(ν) και μοριακής απορροφητικότητας ε(ν) που αντιστοιχούν στις ισχυρότερες ταινίες απορρόφησης του
Li2SO4 και του πολυαιθυλενίου. Για το πολυαιθυλένιο θα γίνει σύγκριση με τις τιμές που θα προκύψουν από την ανάλυση του φάσματος κατοπτρικής ανακλαστικότητας (δες άσκηση 2).
Γ. Mέτρηση Φασμάτων Υπερύθρου Λεπτών Υμενίων
Οπως αναφέρθηκε στην προηγούμενη ενότητα η τεχνική της διαπερατότητας είναι κατάλληλη για την μέτρηση φασμάτων υπερύθρου υμενίων πολυμερών, αρκεί να έχουν πάχος κατάλληλο για την διεύλευση της ακτινοβολίας υπερύθρου. Στην ενότητα αυτή θα ασχοληθούμε με την μέτρηση του φάσματος υμενίων πολυαιθυλενίου (PΕ).
Στο Σχήμα Γ1 παρουσιάζεται το φάσμα ενός σχετικά λεπτού υμενίου PΕ, όπου παρατηρείται ότι οι περισσότερες ταινίες παρουσιάζουν απορρόφηση μικρότερη του 1.5, πλήν της ταινίας στους 2920
cm-1 η οποία πλησιάζει στα όρια κορεσμού. Το Σχήμα Γ2 δείχνει το φάσμα ενός παχύτερου υμενίου PΕ, το οποίο παρουσιάζει το φαινόμενο του κορεσμού στην περιοχή συχνοτήτων των ισχυρότερων κορυφών, δηλαδή περί τους 2920 cm-1 και 1468 cm-1. Συνεπώς, στις φασματικές αυτές περιοχές το υμένιο του Σχήματος Γ2 είναι αδιαφανές, ενώ στο υπόλοιπο μέρος του φάσματος υπερύθρου είναι πλήρως διαφανές.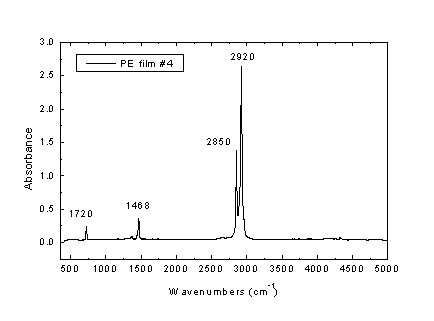
Σχήμα Γ1
: Φάσμα μέσου υπερύθρου λεπτού υμενίου πολυαιθυλενίου.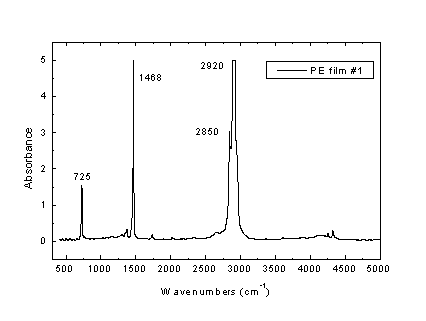 Σχήμα Γ2: Φάσμα μέσου υπερύθρου υμενίου πολυαιθυλενίου που παρουσιάζει κορεσμό των ισχυρότερων ταινιών του, αλλά και κροσσούς συμβολής στην περιοχή χαμηλών συχνοτήτων.
Σχήμα Γ2: Φάσμα μέσου υπερύθρου υμενίου πολυαιθυλενίου που παρουσιάζει κορεσμό των ισχυρότερων ταινιών του, αλλά και κροσσούς συμβολής στην περιοχή χαμηλών συχνοτήτων.
Η ανάπτυξη κροσσών συμβολής στο φάσμα υπερύθρου λόγω πολλαπλών εσωτερικών ανακλάσεων, όταν οι επιφάνειες του υμενίου είναι παράλληλες, επιτρέπει το υπολογισμό του πάχους του υμενίου με χρήση της φασματοσκοπίας
IR. Κροσσοί συμβολής φαίνονται ήδη στην περιοχή χαμηλών συχνοτήτων του φάσματος PΕ#1 (Σχ. Γ2) και είναι πλήρως εμφανείς στο Σχήμα Γ3(α) όπου δίδεται μόνο η φασματική περιοχή έως τους 1000 cm-1.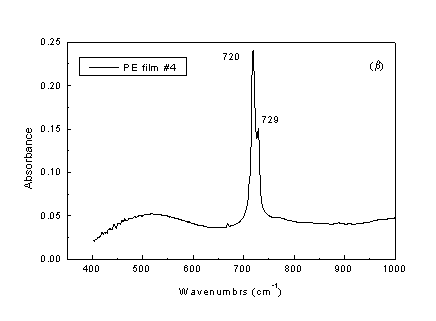

Το πάχος του υμενίου μπορεί να υπολογιστεί από την σχέση:
t=N/[2 n
(ν1-ν2)]
όπου Ν είναι ο αριθμός των κροσσών ανάμεσα σε δύο ακρότατα (μέγιστα ή ελάχιστα) συχνότητας ν
1 και ν2 και n είναι ο δείκτης διάθλασης του υλικού σε φασματική περιοχή που δεν υπάρχουν ταινίες απορρόφησης. Οπως θα δείξουμε στην άσκηση 2 για το πολυαιθυλένιο ισχύει n=1.55. Με το δεδομένο αυτό και τους κροσσούς που εμφανίζονται στο φάσμα του Σχ. Γ3(α) η παραπάνω σχέση οδηγεί στο αποτέλεσμα t» 60 μm για το υμένιο PE#1.Τ
o υμένιο PΕ#4 πρέπει να είναι σημαντικά λεπτότερο του PΕ#1, δεδομένου ότι το φάσμα του παρουσιάζει μόνο ένα κροσσό συμβολής σε συχνότητες χαμηλότερες των 700 cm-1 (δες Σχ. Γ3(β)). Το πάχος του υμενίου PΕ#4 μπορεί να υπολογιστεί έμμεσα χρησιμοποιώντας τα φασματοσκοπικά δεδομένα και πάχος του υμενίου PΕ#1, καθώς και τα φασματοσκοπικά δεδομένα του PΕ#4. Για τον σκοπό αυτό θα κάνουμε χρήση της σχέσης Α=α(ν)t/2.303 (δες ενότητα 3Β) με την υπόθεση ότι η ταινία στους 720 cm-1 παρουσιάζει τον ίδιο συντελεστή απορρόφησης και στα δύο υμένια.
Σκοπός
Στην Ασκηση 1 εξοικειωθήκατε με τις τεχνικές διαπερατότητας στο υπέρυθρο (ελεύθερο υμένιο, και διασπορά σε δισκίο ΚBr). Ωστόσο, σε πολλές περιπτώσεις, η μορφή του δείγματος καθώς και η ανάγκη για τον μή καταστροφικό έλεγχό του επιβάλλουν την χρήση τεχνικών δειγματοληψίας κατά τις οποίες η προσπίπτουσα ακτινοβολία ανακλάται από το δείγμα και δεν το διαπερνά. Η θεωρία και η επίδειξη των τεχνικών αυτών αποτελούν το αντικείμενο της παρούσας άσκησης.1. ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ
1.1. Τεχνική Κατοπτρικής Ανακλαστικότητας (
Specular Reflectance)Η τεχνική αυτή εφαρμόζεται όταν το δείγμα παρουσιάζει λεία επιφάνεια καλής ποιότητος, στην οποία η προσπίπτουσα ακτινοβολία υφίσταται κατοπτρική ανάκλαση (γωνία πρόσπτωσης = γωνία ανακλάσεως).
To μετρούμενο μέγεθος είναι η ανακλαστικότητα του δείγματος που ορίζεται ως ο λόγος R=I/Io όπου Ιο, Ι είναι οι εντάσεις της προσπίπτουσας και ανακλώμενης δέσμης.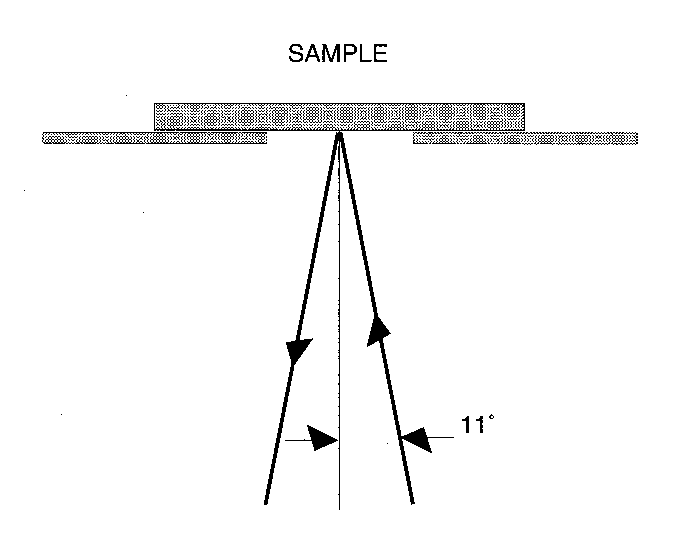
Η φασματοσκοπία κατοπτρικής ανακλαστικότητας προσφέρει πλουσιότατες πληροφορίες σχετικά με τις οπτικές και τις διηλεκτρικές ιδιότητες του δείγματος. μετά από κατάλληλη επεξεργασία των δεδομένων
R(ν). Η επεξεργασία αυτή γίνεται συνήθως με την τεχνική Kramers-Kronig. Το πρώτο βήμα αποτελεί ο υπολογισμός της διαφοράς φάσεως, β(ν), μεταξύ προσπίπτουσας και ανακλώμενης ακτινοβολίας, μέσω του ολοκληρώματος,β(ν)=(2ν/π)
όπου R(v) είναι η μετρούμενη ανακλαστικότητα σαν συνάρτηση της συχνότητας και
r(ν)=[R(ν)]1/2. Στη συνέχεια υπολογίζονται οι οπτικές σταθερές του υλικού, δηλαδή ο δείκτης διάθλασης, n(ν), και ο συντελεστής απορροφητικότητας, k(ν), μέσω των σχέσεων Fresnel:n(ν)=[1- R(ν)] / [1+ R(ν)-2 R
1/2(ν) cos β(ν)]k(ν)=[2 R
1/2(ν) sin β(ν)] / [1+ R(ν)-2 R1/2(ν) cos β(ν)]Το πραγματικό, ε
’(ν) και το φανταστικό, ε’’(ν), μέρος της διηλεκτρικής σταθεράς του δείγματος δίδονται από τις σχέσεις,ε
’(ν) = n2(ν) - k2(ν)
ε
’’(ν)= 2 n(ν) k(ν)Τέλος, ο συντελεστής απορρόφησης του υλικού υπολογίζεται ως εξής,
α(ν) = 4πν k(ν) = 2π ν ε
’’(ν) / n(ν)όπου ν η συχνότητα της ακτινοβολίας υπερύθρου σε cm
-1. Ο συντελεστής απορρόφησης α(ν) συνδέεται με τον συντελεστή μοριακής απορροφητικότητας ε(ν) (δες Ασκηση 1) μέσω της σχεσης
α(ν)=2.303ε(ν)c
όπου c η συγκέντρωση του υλικού.
1.2. Τεχνική Εσωτερικής Ανακλαστικότητας (A
ttenuated Total Reflectance – ATR)Κατ’ αυτήν το δείγμα (δείκτου διάθλασης n
2) βρίσκεται σε επαφή με κρύσταλλο υψηλού δείκτη διάθλασης (n1 > n2) ο οποίος είναι περατός στο υπέρυθρο. Η προσπίπτουσα δέσμη κινείται εντός του κρυστάλλου και έρχεται σε επαφή με το δείγμα στην μεσεπιφάνεια κρυστάλλου-δείγματος.
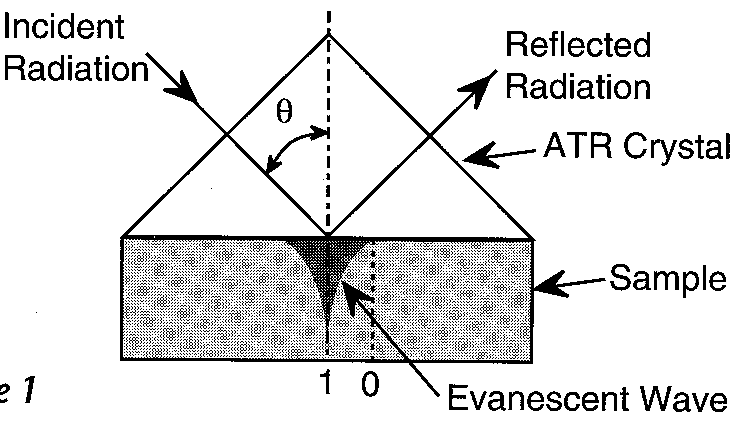
Απαιτείται η καλή επαφή κρυστάλλου-δείγματος, η οποία εξασφαλίζεται συνήθως με εφαρμογή πίεσης. Η προσπίπτουσα δέσμη ανακλάται ολικά στην μεσεπιφάνεια, δηλαδή η γωνία πρόσπτωσης θ είναι μεγα-λύτερη από την χαρακτηριστική γωνία θ
c (critical angle), για την οποία ισχύει,sin
θc = n2/n1Το βάθος διείσδυσης (penetration depth), d
p, ορίζεται ως εκείνο στο οποίο η ένταση της ακτινοβολίας υπερύθρου ελαττώνεται στο Io/e (όπου Ιο είναι ή ένταση της ακτινοβολίας στην μεσεπιφάνεια κρυστάλλου/δείγματος και e είναι η βάση των νεπέρειων λογαρίθμων). Το βάθος διείσδυσης συναρτήσει των δεικτών διάθλασης n1 και n2, της γωνίας πρόσπτωσης θ και του μήκους κύματος της ακτινοβολίας στον αέρα λο, δίδεται από την σχέση:λο
/ dp = 2π n1 [sin2θ-( n2/n1)2] ½H
παραπάνω εξίσωση αναδεικνύει τα κυριότερα πλεονεκτήματα της τεχνικής ATR που είναι:α) η δυνατότητα μή καταστροφικής ανάλυσης υμενίων με σχετικά μεγάλο πάχος, ή πολύ υψηλούς συντελεστές μοριακής απορροφητικότητας
β) η δυνατότητα ανάλυσης πολυστρωματικών δειγμάτων
Τα χαρακτηριστικά τυπικών κρυστάλλων ΑΤ
R και τα αντίστοιχα βάθη διείσδυσης για τρείς διαφορετικές γωνίες πρόσπτωσης δίνονται στον ακόλουθο πίνακα:
|
n1 * |
θ c (ο) ** |
dp (μm) * |
|||
|
θ=30ο |
θ=45ο |
θ=60ο |
|||
|
ZnSe |
2.4 |
38.7 |
- |
2.00 |
1.11 |
|
Si |
3.4 |
26.2 |
2.00 |
0.85 |
0.63 |
|
Ge |
4.0 |
22.0 |
1.20 |
0.66 |
0.51 |
* Οι δείκτες διάθλασης και το βάθος διείσδυσης αναφέρονται τυπικά στους 1000
cm-1, (λο = 10 μm )** n2 = 1.5
Τα βάθη διείσδυσης του παραπάνω πίνακα αναφέρονται σε απλή εσωτερική ανάκλαση. Στην πράξη, η ευαισθησία της τεχνικής ATR αυξάνει σημαντικά με αύξηση του αριθμού εσωτερικών ανακλάσεων, Ν>1. Τούτο επιτυγχάνεται με χρήση μεγαλύτερου κρυστάλλου με σχήμα τραπεζίου ή παραλλεπιπέδου. Σε αυτή την περίπτωση, το φαινόμενο βάθος διείσδυσης (
effective penetration depth) ισούται με Νdp και η ποιότητα του σήματος ενισχύεται σημαντικά. Η παραλλαγή της απλής ανάκλασης εφαρμόζεται μέσω φακοειδών κρυστάλλων σε μικρά δείγματα ή σε αυτά με πορώδεις ή ανώμαλες επιφάνειες τα οποία δεν θα εφάπτοντο αποτελεσματικά στούς συνηθισμένους πρισματικούς κρυστάλλους.
1.3. Τεχνική Ανακλαστικότητας – Απορρόφησης (
Reflection – Absorption)Η τεχνική αυτή αποτελεί παραλλαγή της κατοπτρικής ανακλαστικότητας. Το δείγμα εναποτίθεται υπό μορφή λεπτού υμενίου σε μεταλλική επιφάνεια καλής ανακλαστικότητας.
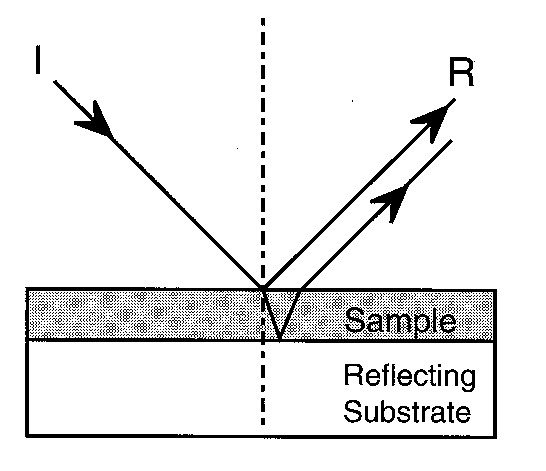
Η ακτινοβολία προσπίπτει (σχεδόν) κάθετα στο δείγμα, το διαπερνά, ανακλάται στην μεταλλική επιφάνεια και επιστρέφοντας μετράται κατά την κατεύθυνση πρόσπτωσης. Το τελικό φάσμα προσομοιάζει αυτό της διαπερατότητας, αλλά αντιστοιχεί σε φαινομενικά διπλάσιο πάχος υλικού. Η ανακλώμενη δέσμη περιέχει συνεισφορά από την κατοπτρική ανακλαστικότητα της μεσεπιφάνειας αέρα-υλικού, αλλά αυτή γίνεται σημαντική μόνο όταν το οπτικό πάχος του υλικού δεν επιτρέπει την ανάκλαση της προσπίπτουσας στην μεταλλική επιφάνεια. Σε αυτή την τελευταία περίπτωση το φάσμα είναι ταυτόσημο με αυτό της κατοπτρικής ανακλαστικότητας, και αναλύεται με τον μετασχηματισμό
Kramers-Kronig.
1.4. Τεχνική Ανακλαστικότητας με Σκέδαση (
Diffuse Reflectance Spectroscopy)Υλικά που παρουσιάζουν μικρό συντελεστή απορρόφησης, αλλά ικανότητα ισχυρής σκέδασης της ακτινοβολίας υπερύθρου λόγω πολλαπλών ανακλάσεων στην επιφάνεια τους, μελετώνται με χρήση της φασματοσκοπίας ανακλάσεως με σκέδαση (Diffuse Reflectance Spectroscopy). Η
τεχνική είναι γνωστή κα με τα αρχικά DRIFT (Diffuse Reflectance Infrared Fourier Transform Spectroscopy). H προσπίπτουσα δέσμη κατευθύνεται με ελλιψοειδές κάτοπτρο στό δείγμα υπό ευρεία στερεά γωνία, ανακλάται από την πορώδη ή κοκκώδη επιφάνεια του υλικού, τυχόν κατοπτρική συνεισφορά αποκόπτεται, και η σκεδαζόμενη ακτινοβολία συλλέγεται επίσης από ελλειψοειδές κάτοπτρο και αναλύεται.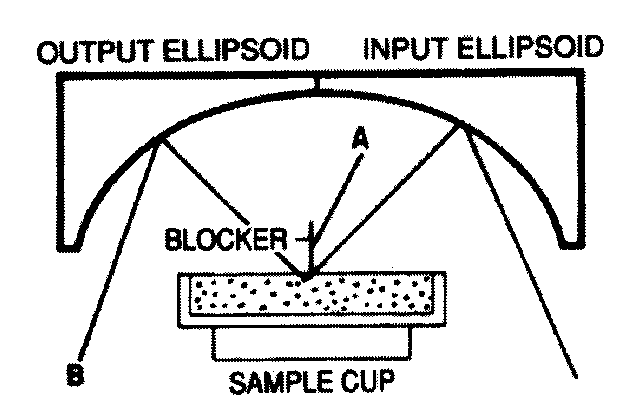
Πλεονεκτήματα της τεχνικής είναι η ευκολία συλλογής δεδομένων απο δείγματα σε μορφή σκόνης, ή με ανώμαλη εξωτερική επιφάνεια, καθώς και η υψηλή ευαισθησία σε ασθενή σήματα (δυνατότητα ανίχνευσης ακόμα και μερικών
ppm).Το μετρούμενο σήμα σχετίζεται με τον συντελεστή μοριακής απορρόφησης του υλικού
a, και τον συντελεστή σκέδασης s μέσω της συνάρτησης Kubelka-Munk, f(R¥ ):f(R¥ ) = (1- R¥ )2/2 R¥ = a/s
όπου R¥ είναι η ανακλαστικότητα που παρουσιάζει “άπειρο” πάχος υλικού (πρακτικά 2-3
mm), Στην πράξη το R¥ αντικαθίσταται από τον λόγο R(sample)/R(standard), όπου R(sample), R(standard) είναι τα φάσματα ανακλάσεως του δείγματος και του υλικού αναφοράς, αντίστοιχα. Ως αναφορά επιλέγεται υλικό που δεν απορροφά στο IR (π.χ. ΚΒr).Από την παραπάνω σχέση προκύπτει ότι ποσοτικές συγκρίσεις μεταξύ φασμάτων (π.χ. εφαρμογές του νόμου
Beer-Lambert) είναι δυνατές μονον εάν αυτά αντιστοιχούν σε δείγματα παρόμοιας φύσης και κοκκομετρίας, ώστε ο συντελεστής s να μπορεί να θεωρηθεί σταθερός.
2. ΠΕΙΡΑΜΑΤΙΚΟ ΜΕΡΟΣ
Για να γνωρίσετε καλύτερα τις τεχνικές ανακλαστικότητας στο υπέρυθρο, τα πλεονεκτήματα και τους περιορισμούς τους, η Ασκηση εστιάζεται στην μελέτη υλικών με συναφή χημική δομή αλλά με διαφορετική μορφολογία. Τα πολυμερή υλικά όπως το πολυαιθυλένιο, με την ποικιλία των μορφών που συναντώνται στην καθημερινή ζωή, είναι κατάλληλα δείγματα για μια τέτοια επίδειξη.
Τα δείγματα
α) πλακίδιο πάχους 1.5
mmβ) φιλμ πάχους 200 μ
mγ) σκόνη
δ) πλαστικοποιημένο αλουμίνιο (υλικό συσκευασίας)
Α) Κατοπτική ανακλαστικότητα
Το δείγμα (α) είναι παχύ, σχετικά δύσκαμπτο, ελαφρά κυρτό, και με λεία επιφάνεια. Οι τεχνικές διαπερατότητας αποκλείονται, και η επαφή του δείγματος με κρύσταλλο πολλαπλών ανακλάσεων δεν θα ήταν καλή χωρίς την άσκηση υπερβολικής πίεσης. Η καταλληλότερη τεχνική δειγματοληψίας είναι αυτή της κατοπτρικής ανακλαστικότητας (
specular reflectance).H
λήψη του φάσματος προϋποθέτει την εγκατάσταση του εξαρτήματος στο φωτόμετρο, την ευθυγράμισή του, και την συλλογή του φάσματος αναφοράς (εδώ, από καθρέπτη αλουμινίου).Το φάσμα κατοπτρικής ανακλαστικότητας του δείγματος α) φαινεται στην Εικόνα Α1. Οι Εικόνες Α2-Α5 περιλαμβάνουν τα φάσματα της διαφοράς φάσεως β(ν), του δείκτη διάθλασης
n(ν) και k(ν), της διηλεκτρικής σταθεράς ε’(ν) και ε’’(ν) και του συντελεστή απορρόφησης α(ν). Ολα έχουν υπολογισθεί από το φάσμα ανακλαστικότητας μέσω των μετασχηματισμών Kramers-Kronig, που συνοψίζονται στο θεωρητικό μέρος.
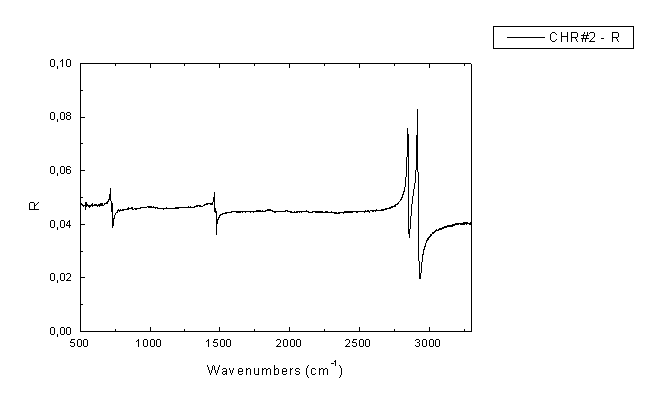
Εικόνα Α1
Φάσμα ανακλαστικότητας πολυαιθυλενίου
Εικόνα Α2
Διαφορά φάσεως β(ν) του προηγούμενου φάσματος
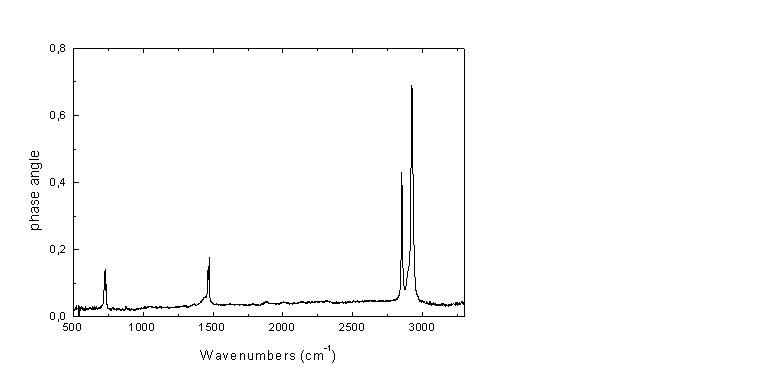
Εικόνα Α3
Δείκτης διαθλάσεως πολυαιθυλενίου
Εικόνα Α4
Διηλεκτρική διαπερατότητα πολυαιθυλενίου
![]()
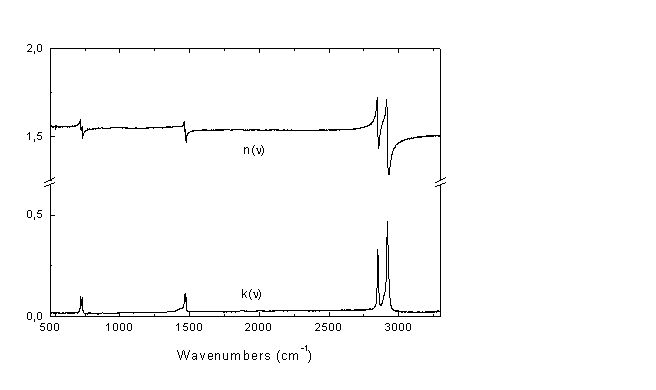
Ειοκόνα Α5
Συντελεστής απορρόφησης πολυαιθυλενίου
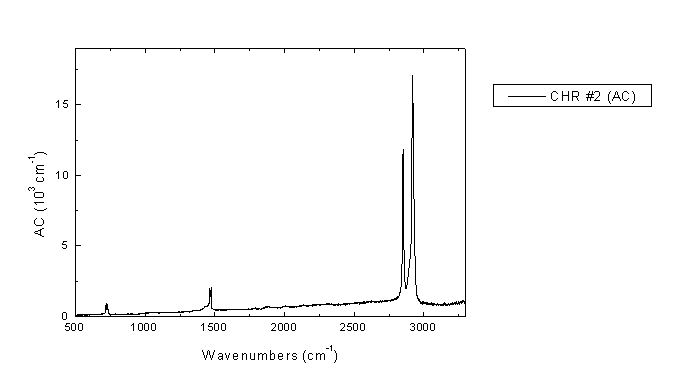
Παρατηρήσεις
:|
Συχνότητα ( cm-1) |
A πόδοση |
|
2918 |
ν as (CH2) – ασύμμετρη έκταση |
|
2850 |
ν s (CH2) - συμμετρική έκταση |
|
1465-1470 |
παραμόρφωση (εκταση-καμψη) |
|
720-730 |
rocking |
Εικόνα Α6
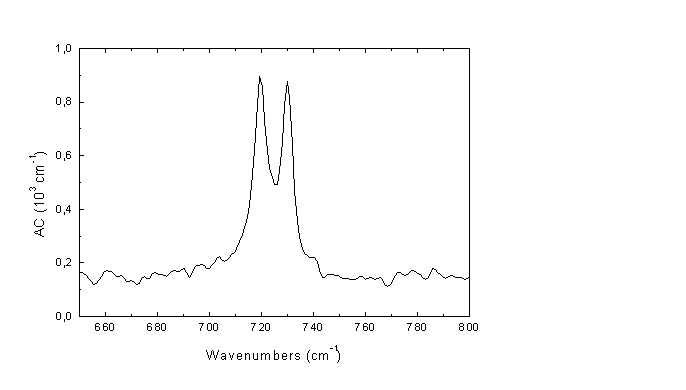
Β) Τεχνική Ολικής Ανάκλασης (ΑΤ
R)Το δείγμα (β) είναι φύλλο πολυαιθυλενίου με κατάλληλα πρόσθετα που χρησιμοποιείται στην κάλυψη θερμοκηπίων. Το πάχος του είναι περίπου 200 μ
m, και συνεπώς είναι παντελώς ακατάλληλο για μετρήσεις διαπερατότητας. Θα μελετήσουμε το φύλλο με τεχνική ATR. H επιλογή του κρυστάλλου (για δεδομένη την γωνία θ=45ο) θα γίνει με τρία κριτήρια: Μεγαλύτερο βάθος διείσδυσης εξασφαλίζεται από το ZnSe. Το κατώφλι συχνοτήτων κάτω από το οποίο ο κρύσταλλος δεν είναι περατός (ZnSe: 450 cm-1, Ge: 650 cm-1, Si: 1000 cm-1) αποκλείει την χρήση Si αν είναι επιθυμητή η παρακολούθηση της κορυφής περί τους 720 cm-1. Το Ge εξασφαλίζει ανεκτό βάθος διείσδυσης (ευαισθησία), και ικανοποιητικό κατώφλι συχνοτήτων, αλλά υπερτερεί ως πρός την αντοχή σε μηχανική καταπόνηση υπό πίεση. Το φάσμα αναφοράς συλλέγεται με την κυψελίδα ΑΤR πλήρη, αλλά χωρίς το φύλλο. Κατόπιν συλλέγονται τα φάσματα και των δύο πλευρών του φύλλου (Εικόνα Β1).E
ικόνα Β1Φάσματα
ATR πολυαιθυλενίου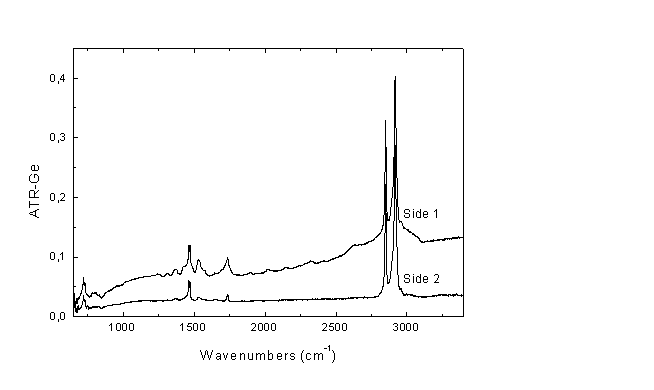
Παρατηρήσεις:
Εικόνα Β2
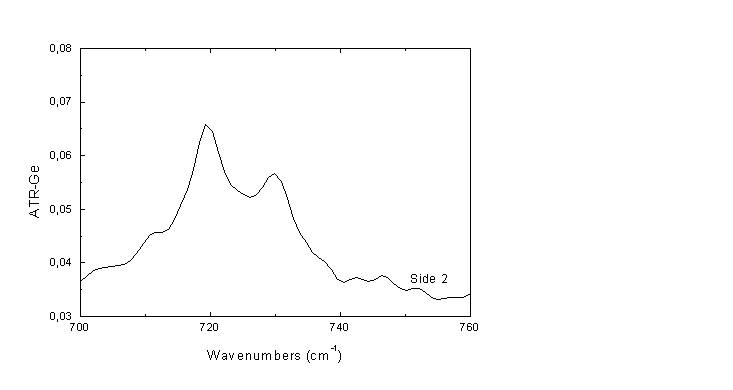
Γ) Ανακλαστικότητα διαχύσεως
Το δείγμα (γ) είναι σε μορφή σκόνης με μέση διάμετρο 20 μ
m. Ακόμα και με άπειρη αραίωση σε KBr, οι κόκκοι δεν είναι περατοί στις φασματικές περιοχές που ενδιαφέρουν. Ο προτιμότερος τρόπος μη-καταστροφικής συλλογής υπέρυθρου φάσματος είναι με ανακλαστικότητα διαχύσεως (DRIFT). Ως υλικό διασποράς, καθώς και αναφοράς, θα χρησιμοποιηθεί KBr. Στην Εικόνα Γ, παρουσιάζονται τα φάσματα DRIFT μετά από μετασχηματισμό Kubelka-Munk.
Εικόνα Γ
επάνω: Φάσμα ανακλαστικότητας διαχύσεως πολυαιθυλενίου
κάτω: το ίδιο μετά από μετασχηματισμό Kubelka Munk
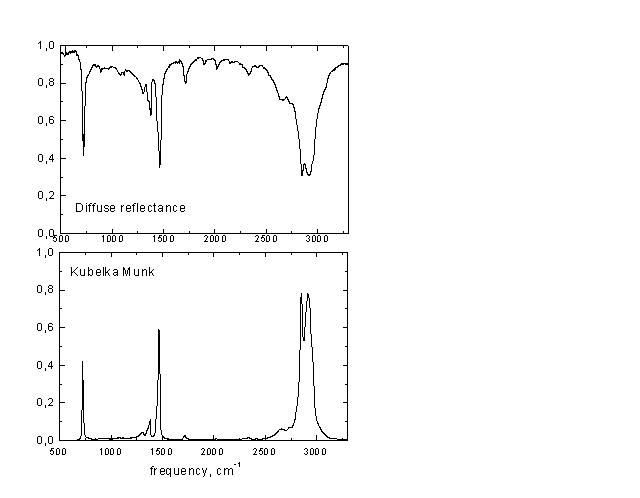
Παρατήρηση:
Δ) Ανακλαστικότητα – Διαπερατότητα
Το δείγμα (δ) είναι πολυστρωματικό υλικό συσκευασίας φαρμακευτικών προϊόντων. Το ενδιάμεσο φύλλο είναι μεταλλικό (αλουμίνιο). Η πολυμερική στοιβάδα έχει τυπικό πάχος 20-80 μ
m, και ενδέχεται να είναι πολυστρωματική. Ενδιαφέρει η δομή του εσωτερικού πολυμερούς φύλλου, ώστε να εκλεγχθεί τυχόν ασυμβατότητά του με το περιεχόμενο σκεύασμα. Η φασματοσκοπική ανάλυση δεν είναι σκόπιμο να αφορά αποκλειστικά την επιφανειακή δομή (οπότε θα χρησιμοποιούσαμε τεχνική ATR). Εκμεταλλευόμενοι την ύπαρξη του φύλλου αλουμινίου, αξιοποιούμε την τεχνική της ανακλαστικότητας- διαπερατότητας, χρησιμοποιώντας ως σήμα αναφορά την ανάκλαση από καθρέπτη αλουμινίου. Το φάσμα παρουσιάζεται στην Εικόνα Δ.
Εικόνα Δ
Φάσμα ανακλαστικότητας – διαπερατότητας
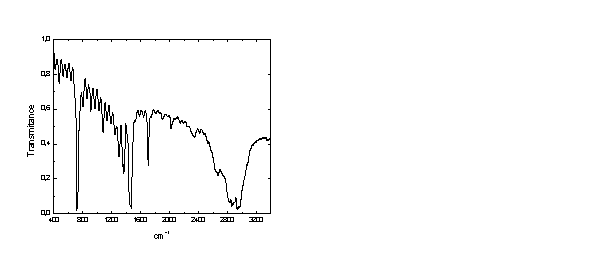
Παρατηρήσεις:
A
ΣΚΗΣΗ 3ME
ΛΕΤΗ ΜΟΡΙΑΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥΜΕ ΦΑΣΜΑΤΟΣΚΟΠΙΑ ΠΟΛΩΜΕΝΟΥ ΥΠΕΡΥΘΡΟΥ
Σκοπός
Η άσκηση αυτή στοχεύει στην εξοικείωση των φοιτητών με την φασματοσκοπία πολωμένου υπερύθρου με μετασχηματισμό Fourier και στην εφαρμογή της για την μελέτη μοριακού προσανατολισμού σε πολυμερικά υλικά που έχουν υποστεί εφελκυσμό. Κατ’ αρχήν παρατίθενται οι γενικές αρχές του φαινομένου του διχρωϊσμού στο υπέρυθρο και η συσχέτισή του με την συνάρτιση προσανατολισμού των μακρομορίων του πολυμερούς. Δίδονται επίσης παραδείγματα πολωμένων φασμάτων υπερύθρου που έχουν μετρηθεί με τις τεχνικές κατοπτρικής ανακλαστικότητας και διαπερατότητας σε πολυμερικά υλικά.
1. ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ
1.1. Ενταση Απορρόφησης στο Υπέρυθρο / Διχρωϊσμός
Η χρησιμότητα της φασματοσκοπίας υπερύθρου στην μελέτη μοριακού προσανατολισμού σε υλικά οφείλεται στο γεγονός ότι η απορρόφηση στο υπέρυθρο ενός μορίου ή μιάς χαρακτηριστικής ομάδος του μορίου είναι ανάλογη του τετραγώνου του εσωτερικού γινομένου της μεταβολής της διπολικής ροπής, Μ
=(¶ μ/¶ x) (transition dipole moment) και του ηλεκτρικού πεδίου, Ε, της προσπίπτουσας ακτινοβολίας,Α
=C [(¶ μ/¶ x).E]2=C (ME)2 cos2γόπου Α η απορρόφηση στο υπέρυθρο, Μ=½
(¶ μ/¶ x)½ , Ε=½ Ε½ και γ η γωνία που σχηματίζει η αναπτυσσόμενη κατά την δόνηση διπολική ροπή με το άνυσμα του ηλεκτρικού πεδίου της ακτινοβολίας. Η σταθερά αναλογίας C είναι C=(8π2NA/3hc)νo, όπου ΝΑ είναι ο αριθμός Avogadro, h η σταθερά Planck, c η ταχύτητα φωτός και νo η συχνότητα της απορροφούμενης ακτινοβολίας υπερύθρου (σε cm-1).Είναι προφανές από την παραπάνω σχέση ότι μέγιστη απορρόφηση στο υπέρυθρο επιτυγχάνεται όταν η ακτινοβολία είναι πολωμένη παράλληλα προς την διπολική ροπή που αναπτύσσεται κατά την δόνηση ενός μορίου, ή μιάς χαρακτηριστικής ομάδος. Αντίθετα, δεν απορροφάται φώς όταν το ηλεκτρικό πεδίο είναι πολωμένο κάθετα προς την διπολική ροπή της δονούμενης ομάδος.
Ορισμένοι τρόποι δόνησης χαρακτηριστικών ομάδων παρουσιάζονται στην Εικ.1 όπου επίσης φαίνεται η κατεύθυνση μεταβολής της αντίστοιχης (αναπτυσσόμενης) διπολικής ροπής. Για παράδειγμα, η δόνηση κάμψεως των μεθυλενομάδων (δ(CH
2)) ενός πολυμερούς παρουσιάζει μέγιστη απορρόφηση για ακτινοβολία υπερύθρου γραμμικά πολωμένη κάθετα προς τον άξονα της αλυσίδας του πολυμερούς (θεωρείστε ότι η αλυσίδα αυτή στην Εικ. 1 είναι οριζόντια).
![]()
Eικόνα 1.
Δονήσεις χαρακτηριστικών ομάδων και κατεύθυνση της αναπτυσσόμενης διπολικής ροπής.
Η παραπάνω εξίσωση δίδει την απορρόφηση μιάς ομάδας ή μορίου που δονείται σε μιά συγκεκριμένη συχνότητα. Η συνολικά μετρούμενη απορρόφηση προκύπτει από το άθροισμα των απορροφήσεων όλων των ομάδων ή μορίων. Εάν τα δονούμενα μόρια είναι τυχαία προσανατολισμένα, όπως συνεπώς και οι σχετικές τους διπολικές ροπές, τότε η μετρούμενη απορρόφηση θα είναι ανεξάρτητη του προσανατολισμού της πόλωσης της προσπίπτουσας ακτινοβολίας. Στην περίπτωση όμως που υπάρχει μερικός, ή ολικός προσανατολισμός των μορίων τότε η μετρούμενη απορρόφηση θα εξαρτάται έντονα από την κατεύθυνση πόλωσης της ακτινοβολίας υπερύθρου ως προς την αναπτυσσόμενη κατά την δόνηση διπολική ροπή. Το φαινόμενο της ανισοτροπίας που παρουσιάζει τότε η απορρόφηση στο υπέρυθρο ονομάζεται διχρωϊσμός και ποσοτικοποιείται από τον λόγο διχρωϊσμού (dichroic ratio),
D = Α| |
/ΑÁόπου Α| | και ΑÁ
είναι οι μετρούμενες απορροφήσεις όταν η ακτινοβολία είναι πολωμένη παράλληλα ή κάθετα προς μία κατεύθυνση αναφοράς, αντίστοιχα. Συνήθως, στα πολυμερή υλικά η δομική ανισοτροπία επάγεται με εφελκυσμό, του οποίου η κατεύθυνση (draw direction) ορίζεται ως κατεύθυνση αναφοράς. Η μέτρηση επομένως του λόγου διχρωϊσμού (D) δίδει ένα ποσοτικό τρόπο για τον καθορισμό του επαγόμενου μοριακού προσανατολισμού σε ένα εφελκυσμένο πολυμερές.
1.2. Μοριακός Προσανατολισμός σε Πολυμερή
Είναι γνωστό ότι η επίτευξη μοριακού προσανατολισμού σε πολυμερή επιφέρει σημαντική βελτίωση των ιδιοτήτων τους. Συνήθως, μοριακός προσανατολισμός επιτυγχάνεται με εφελκυσμό του πολυμερούς σε θερμοκρασίες πλησίον της θερμοκρασίας υαλώσεως (Tg). Η διερεύνηση της ύπαρξης μοριακού προσανατολισμού και της εξάρτησής του από τις χρησιμοποιούμενες πειραματικές συνθήκες (είδος μεθόδου, θερμοκρασία, χρόνος παραμονής του υλικού και πάχος) αποτελεί κεντρικό
πρόβλημα στις σχετικές βιομηχανίες, με σημαντικό φυσικά οικονομικό αντίκτυπο.Οπως έχουμε δεί στην προγηγούμενη ενότητα η φασματοσκοπία υπερύθρου μπορεί να χρησιμοποιηθεί για την διερεύνηση της ύπαρξης μοριακού προσανατολισμού. Τούτο απαιτεί την μέτρηση φασμάτων υπερύθρου με ακτινοβολία πολωμένη παράλληλα (Α| | ) και κάθετα (ΑÁ ) προς την κατεύθυνση εφελκυσμού του πολυμερούς (draw direction), πράγμα που οδηγεί στον υπολογισμό του διχρωϊκού λόγου, D=Α| | /ΑÁ
.Εάν υποθέσουμε ότι f
p είναι το ποσοστό των μακρομορίων του πολυμερούς που προσανατολίζονται παράλληλα προς τον άξονα εφελκυσμού (και επομένως 1- fp είναι το ποσοστό των τυχαίως προσανατολισμένων μορίων) τότε η θεωρία προβλέπει ότι:D = [fp cos2
ψ+(1/3) (1-fp)] / [(1/2) fp sin2ψ+(1/3) (1-fp)]όπου ψ είναι η γωνία που σχηματίζει η αναπτυσσόμενη κατά την δόνηση διπολική ροπή (μ) με τον άξονα του πολυμερούς.
ψ
μ
Εάν θέσουμε D
o=2 cot2ψ, τότε η παραπάνω σχέση μετασχηματίζεται στην:fp = [(D-1) (Do+2)] / [(D+2) (Do-1)]
Προκειμένου περί δονήσεων για τις οποίες η διπολική ροπή αναπτύσσεται κάθετα προς τον άξονα του πολυμερους (ψ=90ο) η προηγούμενη σχέση απλοποιείται ως εξής:
fp = 2 (1-D) / (D+2)
ενώ για ψ=0ο προκύπτει:
fp = (D-1) / (D+2)
Επομένως, μέτρηση του λόγου D και γνώση της φύσης των υπό μελέτη μοριακών δονήσεων επιτρέπει τον υπολογισμό του βαθμού μοριακού προσανατολισμού f
p μέσω της παραπάνω σχέσεως.Συχνά, ο προσανατολισμός των μακρομορίων ως προς κάποιον άξονα αναφοράς εκφράζεται μέσω της συνάρτησης προσανατολισμού, f(θ), η οποία αναπτύσσεται σε πολυώνυμα
Legendre:f(θ) = (1/2π) Σ (n+1/2) <
Pn(cosθ)> Pn(cosθ)όπου
Pn(cosθ) είναι το πολυώνυμο Legendre n-τάξεως, δηλαδή:P2(cos
θ) = (3cos2θ-1)/2P4(cos
θ) = (35cos4θ-30cos2θ +3)/8, κ.λπ.και θ είναι η γωνία που σχηματίζει ο άξονας του πολυμερούς με την κατεύθυνση αναφοράς (π.χ. εφελκυσμού).
θ
draw direction
Αποδεικνύεται ότι η μέση τιμή του πολυωνύμου
Legendre δευτέρας τάξεως (second-order Legendre polynomial) συνδέεται με τον διχρωϊκό λόγο D ως εξής:< P2(cos
θ)> = [3 < cos2θ> - 1]/2 = [(D-1) (Do+2)] / [(D+2) (Do-1)]Προκύπτει ότι <
P2(cosθ)> =fp, δηλαδή ο όρος αυτός δίδει το κλάσμα των μακρομορίων που προσανατολίζονται παράλληλα προς την κατεύθυνση εφελκυσμού. Συνεπώς, ο όρος < P2(cosθ)> της συνάρτησης προσανατολισμού των μακρομορίων μπορεί να υπολογιστεί από μετρήσεις φασμάτων υπερύθρου με πολωμένο φώς. Ο υπολογισμός του όρου < P4(cosθ)> απαιτεί μετρήσεις πολωμένου Raman (σχετική άσκηση θα γίνει σε εργαστήριο άλλου Ερευνητικού Κέντρου).Από την παραπάνω σχέση προκύπτουν εύκολα οι εξής ειδικές περιπτώσεις που αφορούν την φασματοσκοπία πολωμένου υπερύθρου:
1.3. Πολωμένα Φάσματα Πολυμερών στο Υπέρυθρο
 Στην ενότητα αυτή παρουσιάζονται ορισμένα χαρακτηριστικά παραδείγματα πολωμένων φασμάτων υπερύθρου πολυμερών υλικών, που έχουν μελετηθεί πρόσφατα στο Εργαστήριο Φασματοσκοπίας του Ινστιτούτου Θεωρητικής και Φυσικής Χημείας (ΙΘΦΧ) του ΕΙΕ.
Στην ενότητα αυτή παρουσιάζονται ορισμένα χαρακτηριστικά παραδείγματα πολωμένων φασμάτων υπερύθρου πολυμερών υλικών, που έχουν μελετηθεί πρόσφατα στο Εργαστήριο Φασματοσκοπίας του Ινστιτούτου Θεωρητικής και Φυσικής Χημείας (ΙΘΦΧ) του ΕΙΕ.
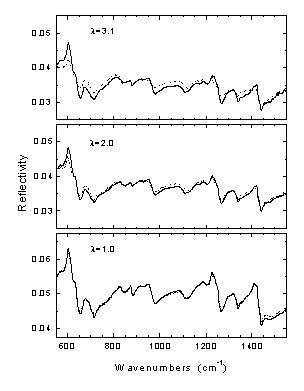
Εικόνα 2.
Πολωμένα φάσματα κατοπτρικής ανακλαστικότητας στο υπέρυθρο δειγμάτων PVC που έχουν υποστεί εφελκυσμό. Ο βαθμός εφελκυσμού δίδεται από την παράμετρο λ (draw ratio) και ισούται με τον λόγο του τελικού προς το αρχικό μήκος του δείγματος. Τα συνεχή φάσματα έχουν μετρηθεί με την ακτινοβολία υπερύθρου να είναι πολωμένη παράλληλα προς τον άξονα εφελκυσμού του δοκιμίου, ενώ τα εστιγμένα φάσματα αντιστοιχούν σε πόλωση της ακτινοβολίας κάθετα προς τον άξονα εφελκυσμού.To PVC (Polyvi
nyl Chloride) αποτελεί ένα από τα σπουδαιότερα δομικά πολυμερή που χρησιμοποιούνται εκτενώς, και συνεπώς η μελέτη του προβλήματος του μοριακού του προσανατολισμού είναι κεντρικής σημασίας. Τα βιομηχανικά δείγματα που μελετήθησαν στο εργαστήριο φασματοσκοπίας του ΙΘΦΧ είχαν πάχος της τάξεως 2-5 mm και ήταν επομένως αδύνατη η εφαρμογή της φασματοσκοπίας διαπερατότητος. Για τον λόγο αυτό χρησιμοποιήθηκε η τεχνική της κατοπτρικής ανακλαστικότητας με γωνία πρόσπτωσης 11ο (δες άσκηση 2). Χαρακτηριστικά φάσματα ανακλαστικότητας φαίνονται στην Εικ. 2 για βιομηχανικά δείγματα που υπέστησαν διαφορετικό βαθμό εφελκυσμού (λ=μήκος δείγματος μετά τον εφελκυσμό / αρχικό μήκος δείγματος).Παρατηρείται ότι για το δείγμα που δεν έχει υποστεί εφελκυσμό (λ=1) τα μετρούμενα φάσματα είναι ανεξάρτητα της πόλωσης της ακτινοβολίας υπερύθρου, όπως και αναμένεται. Αύξηση όμως του λ επιφέρει σταδιακά διάκριση των φασμάτων, δηλ. εξάρτηση από τον τρόπο πόλωσης της ακτινοβολίας. Τούτο αποτελεί άμεση ένδειξη του επαγόμενου προσανατολισμού των μακρομορίων του PVC λόγω εφελκυσμού του δείγματος.
Περαιτέρω ποσοτικοποίηση των αποτελεσμάτων γίνεται με ανάλυση των φασμάτων ανακλαστικότητας με την τεχνική Kramers-Kronig (δες άσκηση 2) που οδηγεί στον υπολογισμό των φασμάτων απορρόφησης. Από τα φάσματα απορρόφησης υπολογίζεται ο διχρωϊκός λόγος D για χαρακτηριστικές δονήσεις του PVC, όπως είναι η δόνηση έκτασης της ομάδας C-Cl (614 cm
-1 και 635 cm-1 για άμορφες και κρυσταλλικές περιοχές του PVC, αντίστοιχα). Στη συνέχεια μπορεί να υπολογιστεί το κλάσμα fp (βαθμός προσανατολισμού) σαν συνάρτιση του βαθμού εφελκυσμού (λ) των δοκιμίων PVC. Στην περίπτωση αυτή ευρέθη ότι το fp αυξάνει από μηδέν έως περίπου 30% για την περιοχή εφελκυσμού 0= λ= 3.0.Σε ορισμένες περιπτώσεις το εφελκυσμένο πολυμερές είναι διαθέσιμο στη μορφή λεπτού σχετικά υμενίου. Τότε, η ύπαρξη και ο βαθμός μοριακού προσανατολισμού μπορούν να δερευνηθούν με εφαρμογή της τεχνικής της διαπερατότητας (δες άσκηση 1), με χρήση πολωμένης ακτινοβολίας υπερύθρου. Ενα τέτοιο παράδειγμα δίδεται στην Εικ. 3 για ένα πολυεστερικό δείγμα (
PES) που έχει βαθμό εφελκυσμού λ=1.5.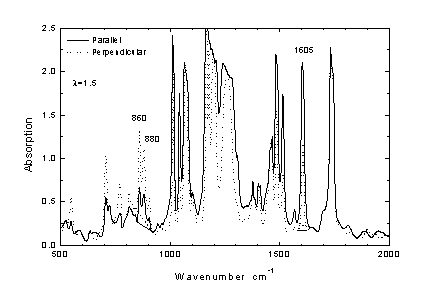
Εικόνα 3.
Πολωμένα φάσματα απορρόφησης στο υπέρυθρο υμενίου πολυεστέρος (PES) με βαθμό εφελκυσμού λ=1.5. Το συνεχές φάσμα έχει μετρηθεί με πόλωση της ακτινοβολίας παράλληλη προς τον άξονα εφελκυσμού, ενώ το εστιγμένο φάσμα αντιστοιχεί στην κάθετη πόλωση.
Το πάχος του πολυεστερικού υμενίου είναι σχετικά μεγάλο (» 30 μ
m) με αποτέλεσμα οι περισσότερες ταινίες του φάσματος να παρουσιάζουν έντονο κορεσμό (δες άσκηση 1). Παρά ταύτα υπάρχουν ορισμένες ταινίες του φάσματος που μπορούν να χρησιμοποιηθούν ως δείκτες του επαγόμενου μοριακού προσανατολισμού. Ως πλέον κατάλληλες έχουν επιλεγεί η ταινία στους 1605 cm-1 και η διπλέτα των 860/880 cm-1. Η πρώτη ταινία αποδίδεται στην δόνηση έκτασης του δεσμού C=C, με διπολική ροπή σχεδόν παράλληλη προς τον άξονα της μακρομοριακής αλυσίδας (ψ=0ο). Η διπλέτα των 860/880 cm-1 οφείλεται στην δόνηση κάμψης του δεσμού C-H ως προς το επίπεδο το βενζοϊκού δακτυλίου, η δε αναπτυσσόμενη διπολική ροπή είναι κάθετη προς την πολυμερική αλυσίδα (ψ=90ο). Οι διαφορές που παρουσιάζουν οι δείκτες/ταινίες που επιλέγονται, ως προς τον προσανατολισμό της διπολικής τους ροπής, εξηγούν άμεσα τις παρατηρούμενες διαφορές στις εντάσεις των ταινιών που επιφέρει η αλλαγή στην πόλωση της υπέρυθρης ακτινοβολίας (Εικ. 3).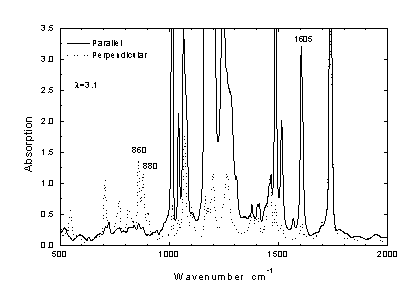
Εικόνα 4.
Αύξηση του βαθμού εφελκυσμού (λ=3.1) του πολυεστερικού υμενίου (PES) επιφέρει έντονες αλλαγές στα πολωμένα φάσματα υπερύθρου. Ιδιαίτερα ευαίσθητες στην πόλωση της ακτινοβολίας υπερύθρου είναι οι ταινίες των 1605 και 860/880 cm-1.
Αύξηση του βαθμού εφελκυσμού του πολυεστερικού υμενίου επιφέρει ακόμη μεγαλύτερες μεταβολές στις εντάσεις των ταινιών στους 1605
cm-1 και 860/880 cm-1 καθώς αλλάζει η πόλωση της προσπίπτουσας υπέρυθρης ακτινοβολίας. Ενα χαρακτηριστικό παράδειγμα δίδεται στην Εικ. 4 για βαθμό εφελκυσμού λ=3.1. Οπως παρατηρείται, η ταινία των 1605 cm-1 παρουσιάζει σχεδόν μηδενική ένταση όταν η πόλωση της ακτινοβολίας είναι κάθετη προς την κατεύθυνση εφελκυσμού, ενώ αντίθετα οι ταινίες στους 860/880 cm-1 παρουσιάζουν την μέγιστη ένταση στην κάθετη πόλωση. Το γεγονός αυτό υποδηλώνει τον σχεδόν πλήρη προσανατολισμό των πολυεστερικών αλυσίδων για το συγκεκριμένο δοκίμιο. Για περισσότερες λεπτομέρειες που αφορούν την ανάλυση των φασμάτων υπερύθρου και Raman των δειγμάτων αυτών (PES) ο αναγνώστης μπορεί να συμβουλευτεί την αναφορά [4].Τα παραπάνω παραδείγματα σκιαγραφούν τις μεγάλες δυνατότητες που παρέχει η φασματοσκοπία πολωμένου υπερύθρου σε θέματα μελέτης μοριακού προσανατολισμού σε υλικά, και στις σχετικές μεταβολές που επιφέρουν οι διάφορες φυσικές ή και χημικές διεργασίες.
ΒΙΒΛΙΟΓΡΑΦΙΑ
2. ΠΕΙΡΑΜΑΤΙΚΟ ΜΕΡΟΣ
Στο πειραματικό μέρος της παρούσας άσκησης θα ασχοληθούμε με την μέτρηση πολωμένων φασμάτων στο υπέρυθρο σε δείγματα εφελκυσμένων δοκιμίων του πολυμερούς
Poly Ethylene Terephthalate (PET), (-O-CO-C6H4-CO-O-CH2-CH2-)n. Στη συνέχεια θα γίνει αποτίμηση των φασματοσκοπικών δεδομένων, με απώτερο στόχο την διερεύνηση του επαγόμενου προσανατολισμού των μακρομορίων του ΡΕΤ με αύξηση του βαθμού εφελκυσμού του δοκιμίου.Η παρασκευή των δοκιμίων έγινε από την ομάδα του Ερευνητικού Ινστιτούτου Χημικής Μηχανικής και Χημικών Διεργασιών Υψηλής Θερμ
oκρασίας (ΕΙΧΜΧΔΥΘ) του ΙΤΕ Πάτρας, χρησιμοποιώντας εμπορικό ΡΕΤ ως πρώτη ύλη. Η ανάπτυξη των υμενίων, πάχους 35-40 μm, έγινε με τήξη και συμπίεση του υλικού μεταξύ πλακών Teflon σε θερμοκρασία 300 0C. Στη συνέχεια, τεμάχια του αρχικού υμενίου υπέστησαν εφελκυσμό σε θερμοκρασία 84 0C (Τg=74 0C) και με ταχύτητα 12 cm/min. Με την μέθοδο αυτή προέκυψαν δοκίμια ΡΕΤ με βαθμό εφελκυσμού λ=1, 2, 3.2 και 4. Τα δοκίμια αυτά μελετώνται στην συνέχεια με φασματοσκοπία πολωμένου υπερύθρου.Για την μέτρηση των πολωμένων φασμάτων υπερύθρου χρησιμοποιείται κατάλληλος πολωτής (
KRS-5 wire-grid polarizer), ο οποίος τοποθετείται πριν από το δείγμα και κάθετα προς την δέσμη της υπερύθρου ακτινοβολίας. Στην παρούσα άσκηση θα μετρηθούν δύο φάσματα απορρόφησης (Αbsorption) για κάθε δοκίμιο ΡΕΤ. Το ένα φάσμα θα μετρηθεί με πόλωση της ακτινοβολίας παράλληλη προς τον άξονα εφελκυσμού του δείγματος, και στη συνέχεια, χωρίς να μετακινηθεί το δείγμα, θα στρέφεται το επίπεδο πόλωσης της ακτινοβολίας κατά 900 και θα επαναλαμβάνεται η μέτρηση. Ως φάσματα αναφοράς θα χρησιμοποιηθούν τα φάσματα διαπερατότητας του πολωτή με παράλληλη και κάθετη πόλωση της ακτινοβολίας.Στο Σχήμα 1 παρουσιάζονται πολωμένα φάσματα του ΡΕΤ που έχουν μετρηθεί σε δοκίμιο πριν υποστεί εφελκυσμό, δηλαδή με βαθμό εφελκυσμού λ=1. Ο βαθμός προσανατολισμού των μακρομορίων του πολυμερούς στο δοκίμιο αυτό αναμένεται να είναι μηδενικός. Το γεγονός αυτό επιβεβαιώνεται άμεσα από το φασματοσκοπικό αποτέλεσμα, δηλαδή την μή εξάρτηση των φασμάτων υπερύθρου από την πόλωση της ακτινοβολίας (δες Σχ. 1). Παρά το φαινόμενο κορεσμού που παρουσιάζουν οι περισσότερες ταινίες του φάσματος, παρατηρείται ότι η αλληγή πόλωσης της ακτινοβολίας υπερύθρου δεν επηρεάζει το φάσμα.
Ο εφελκυσμός όμως του δοκιμίου προκαλεί βαθμιαίες μεταβολές στις σχετικές εντάσεις των πολωμένων φασμάτων υπερύθρου του ΡΕΤ, όπως φαίνεται χαρακτηριστικά στο Σχήμα 2 για το δοκίμιο με τον μεγαλύτερο βαθμό εφελκυσμού (λ=4). Για την ποσοτικοποίηση του φαινομένου αυτού θα χρησιμοποιήσουμε ορισμένες ταινίες του ΡΕΤ με βάση τα κριτήρια:
Οι χρησιμοποιούμενες ταινίες ‘δείκτες’ και η απόδοσή τους σε δονήσεις χαρακτηριστικών ομάδων του ΡΕΤ δίδονται στον Πίνακα 1.
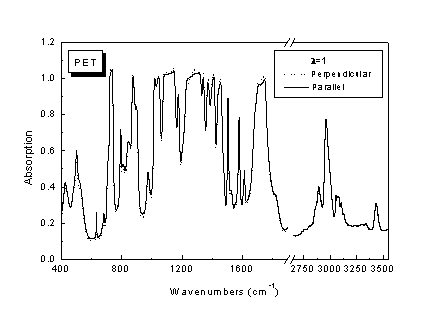
Σχήμα 1. Πολωμένα φάσματα απορρόφησης στο υπέρυθρο υμενίου ΡΕΤ με βαθμό εφελκυσμού λ=1. Οι δύο διαφορετικές πολώσεις της ακτινοβολίας οδηγούν στο ίδιο πρακτικά φάσμα.
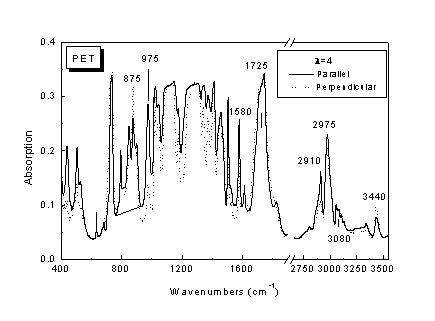
Σχήμα 2.
Πολωμένα φάσματα απορρόφησης στο υπέρυθρο υμενίου ΡΕΤ με βαθμό εφελκυσμού λ=4. Παρατηρείται ότι ορισμένες ταινίες του φάσματος παρουσιάζουν επιλεκτικότητα ως προς την πόλωση της προσπίπτουσας ακτινοβολίας υπερύθρου.Πίνακας 1.
Ταινίες του ΡΕΤ που παρουσιάζουν ευαισθησία στην πόλωση της ακτινοβολίας υπερύθρου.
|
Ταινία ( cm-1) |
Απόδοση ταινίας και πόλωση |
|
875 |
εκτός δακτυλίου δόνηση κάμψης του δεσμού C-Hπόλωση: ^ |
|
975 |
δόνηση έκτασης των δεσμών C-O και O-CH2πόλωση: ^ & | | |
|
1580 |
δόνηση έκτασης των δεσμών C-C του δακτυλίουπόλωση: | | |
|
3440 |
υπέρτονος της δόνησης έκτασης του δεσμού C=O, 2ν(C=O)πόλωση: ^ |
Σημείωση: Οι ενδείξεις ^ και | | υποδηλώνουν μεταβολή της διπολικής ροπής κάθετα και παράλληλα, αντίστοιχα, προς την μακρομοριακή αλυσίδα.
Οπως φαίνεται στην Εικ. 1 η αναπτυσσόμενη διπολική ροπή κατά την δόνηση έκτασης το δεσμού
C=O της πολυεστερικής ομάδας ( -Ο-CO-) του ΡΕΤ αναμένεται να είναι κάθετη προς τον άξονα του μακρομορίου. Η δόνηση αυτή, ν(C=O), είναι ενεργή στους 1725 cm-1 (Σχ. 1 και 2) αλλά η μεγάλη ενεργότητά της έχει ως αποτέλεσμα τον κορεσμό της σε όλα τα υπό μελέτη δοκίμια. Το μειονέκτημα αυτό μετατρέπεται σε πλεονέκτημα όσον αφορά την δυνατότητα καταγραφής του υπέρτονου 2ν(C=O). Ο υπέρτονος αυτός παρουσιάζεται στους 3440 cm-1, αντί των 3450 cm-1 (λόγω αναρμονικότητας), και αναμένεται να παρουσιάζει τα ίδια χαρακτηριστικά πόλωσης με την βασική δόνηση (ν(C=O)). Οπως παρατηρείται στο Σχ. 2 και η ταινία των 875 cm-1 παρουσιάζει πόλωση κάθετη προς την μακρομοριακή αλυσίδα.Χαρακτηριστική ταινία του ΡΕΤ με πόλωση παράλληλη προς την μακρομοριακή αλυσίδα είναι αυτή των 1580
cm-1, η οποία οφείλεται στην δόνηση έκτασης των δεσμών C-C του δακτυλίου. Τέλος, η ταινία των 975 cm-1 επιλέγεται ως χαρακτηριστική ταινία του ΡΕΤ με ενδιάμεση πόλωση.Από τα πολωμένα φάσματα υπερύθρου των δοκιμίων ΡΕΤ υπολογίζεται ο διχρωϊκός λόγος, D=Α| | /ΑÁ , για τις ταινίες ‘δείκτες’ του Πίνακα 1, όπου Α| | και ΑÁ
είναι οι μετρούμενες εντάσεις με πόλωση παράλληλη (½ ½ ) και κάθετη (^ ) προς τον άξονα εφελκυσμού του δοκιμίου. Τα αποτελέσματα δίδονται στο Σχήμα 3 ως προς τον βαθμό εφελκυσμού (draw ratio, λ) των δοκιμίων. Με βάση τα χαρακτηριστικά πόλωσης που παρουσιάστηκαν παραπάνω, η μείωση του διχρωϊκού λόγου των ταινιών 875 και 3440 cm-1 και η παράλληλη αύξηση του διχρωϊκού λόγου της ταινίας των 1580 cm-1, καταδεικνύουν την τάση προσανατολισμού των μακρομοριακών αλυσίδων παράλληλα προς τον άξονα εφελκυσμού των δοκιμίων. Ενδεικτική της τάσης προσανατολισμού είναι και η συμπεριφορά της ταινίας των 975 cm-1 (Σχ. 2), της οποίας ο λόγος D εμφανίζει αρχικά αύξηση και στην συνέχεια ελάττωση με αύξηση του λ.
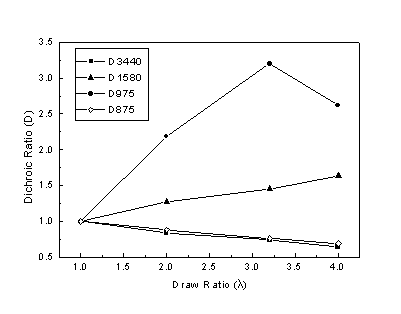
Σχήμα 3.
Διχρωϊκός λόγος (D) χαρακτηριστικών ταινιών του ΡΕΤ ως προς τον βαθμό εφελκυσμού (λ) των δοκιμίων.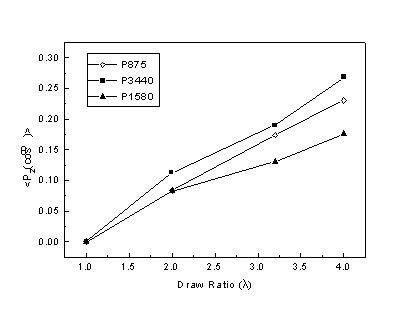
Σχήμα 4. Κλάσμα προσανατολισμού
(< P2(cosθ)> ) ως προς τον βαθμό εφελκυσμού (λ) δοκιμίων ΡΕΤ.
Από τον διχρωϊκό λόγο των ταινιών 3440, 1580 και 875
cm-1, για τις οποίες υπάρχει γνώση για την κατεύθυνση μεταβολής της διπολικής ροπής, υπολογίζεται το κλάσμα των μακρομορίων που προσανατολίζονται παράλληλα προς την κατεύθυνση εφελκυσμού (< P2(cosθ)> ή fp), κάνοντας χρήση των αντίστοιχων εξισώσεων (δες ενότητα 1.2). Τα σχετικά αποτελέσματα δίδονται στο Σχήμα 4, όπου φαίνεται μεταβολή του κλάσματος προσανατολισμού των μακρομορίων από μηδέν έως περίπου 25% καθώς αυξάνει ο βαθμός εφελκυσμού του δοκιμίου στην περιοχή 0£ λ£ 4.Οπως παρατηρείται στο Σχ. 4 οι τρείς ταινίες (3440, 1580 και 875
cm-1) δεν δίδουν το ίδιο ακριβώς κλάσμα προσανατολισμού. Τούτο μπορεί να οφείλεται: (α) σε πειραματικό σφάλμα, π.χ. χρήση διαφορετικής γραμμής αναφοράς (base line) και (β) στο γεγονός ότι ο προσανατολισμός της αναπτυσσόμενης διπολικής ροπής μπορεί να αποκλείνει από τις 900 (ταινίες 3440 και 875 cm-1) και 00 (ταινία 1580 cm-1), που χρησιμοποιήθηκαν για τον υπολογισμό του βαθμού μοριακού προσανατολισμού.
Σκοπός
Η Ασκηση 4 σας εισάγει στις ιδιαιτερότητες της φασματοσκοπίας εγγύς υπερύθρου, στα πλεονεκτήματα και τα μειονεκτήματά της. Γίνεται ειδική αναφορά στό εύρος των βιομηχανικών εφαρμογών, και επιδεικνύονται φασματοσκοπικές μεθοδολογίες ομαδοποίησης - ταυτοποίησης και προσδιορισμού της σύστασης πολυμερών.
1. ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ
Α. Φασματοσκοπία στο εγγύς υπέρυθρο
Η φασματική περιοχή του εγγύς υπερύθρου (
near infrared, NIR) εκτείνεται από τα συμβατικά όρια του υπερύθρου (4.000 cm-1 ή 2.5 μm) μέχρι το ερυθρό του ορατού φάσματος (12.800 cm-1 ή 780 nm). Η ενεργότητα των περισσότερων υλικών σε αυτή την περιοχή του ηλεκτρομαγνητικού φάσματος είναι ασθενής δίοτι οφείλεται στους υπέρτονους και συνδυασμούς των δονητικών μεταπτώσεων. Η κβαντισμένη δονητική ενέργεια ενός αρμονικού ταλαντωτή δίνεται από την σχέση:Ε=(υ + ½)
hνόπου υ ο δονητικός κβαντικός αριθμός (υ=0, 1, 2, ...) και
h η σταθερά του Planck.Ως υπέρτονοι χαρακτηρίζονται οι μεταπτώσεις από υ=0 σε υ=2 ή μεγαλύτερο. Στίς μεταπτώσεις συνδυασμού ένα φωτόνιο διεγείρει δύο (ή περισσότερες) διαφορετικές μεταπτώσεις, υ
1=0 ® υ1=1 και υ2=0 ® υ2=1.Τυπικά, οι υπέρτονοι δόνησης με ιδιοσυχνότητα ν αναμένονται σε συχνότητες 2ν (2ος υπέρτονος), 3ν (τρίτος) κλπ. Ομοίως, η μετάπτωση συνδυασμού δονήσεων με ιδιοσυχνότητες ν
1 και ν2, αναμένεται σε συχνότητα (ν1 + ν2). Υπενθυμίζεται ότι οι μεταπτώσεις αυτές είναι απαγορευμένες για τον αρμονικό ταλαντωτή (δες Ασκηση 1). Η όποια ενεργότητά τους είναι συνέπεια της αναρμονικότητας του δυναμικού, και γι αυτό οι υπέρτονοι και συνδυασμοί έχουν χαμηλούς συντελεστές απορρόφησης και εμφανίζονται σε συχνότητες χαμηλότερες από αυτές που θα αντιστοιχούσαν σε αρμονικό ταλαντωτή. Οι δονήσεις ανώτερων υπερτόνων (και συνδυασμών) έχουν συχνά 10-100 φορές χαμηλότερο συντελεστή απορρόφησης από τις αντίστοιχες δονητικές μεταπτώσεις χαμηλότερης τάξης. Η ελάττωση αυτή του συντελεστή απορρόφησης είναι συνάρτηση της αναρμονικότητας τού δονητή. Αντίστοιχα, το βάθος διείσδυσης της ακτινοβολίας είναι 10-100 φορές μεγαλύτερο στους ανώτερους υπέρτονους, και στις περισσότερες περιπτώσεις είναι δυνατή η συλλογή δεδομένων χωρίς καμμία προετοιμασία του δείγματος.Στήν Εικόνα Α, περιλαμβάνεται το φάσμα απορρόφησης πολυαιθυλενίου στο
NIR.
Eικόνα
A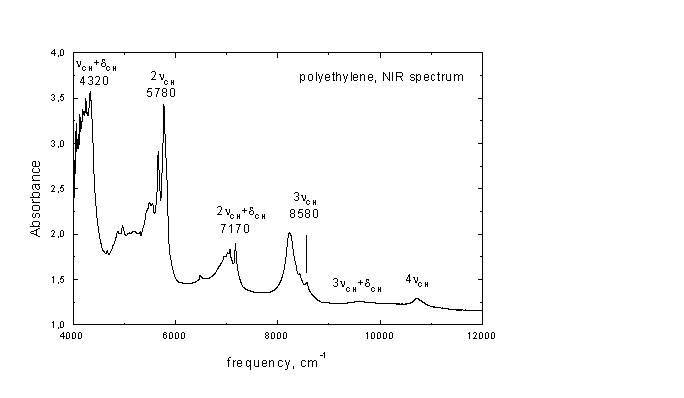
Εντονες απορροφήσεις παρατηρούνται σε διακριτές φασματικές περιοχές. Η έντασή τους φθίνει αυξανόμενης της συχνότητας, όπως θα αναμενόταν για υπέρτονους ανώτερης τάξεως. Η απλότητα του φάσματος
MIR του πολυαιθυλενίου (νCH2 » 2900 cm-1, δCH2 » 1465 cm-1, δες Ασκηση 2) επιτρέπει την ταυτοποίηση των κυριότερων κορυφών NIR.
|
Περιοχή απορρόφησης NIR (cm-1) |
Απόδοση |
|
4100-4300 |
ν CH2 + δCH2 |
|
5600-5800 |
2 ν CH2 |
|
7000-7200 |
2 ν CH2 + δCH2 |
|
8400-8600 |
3 ν CH2 |
|
9500-10000 |
3 ν CH2 + δCH2 |
|
10700-11000 |
4 ν CH2 |
Από τα παραπάνω προκύπτουν δύο κύριες παρατηρήσεις που αφορούν την ενεργότητα δονητικών μεταπτώσεων στό
NIR:α) Το
NIR είναι εξαιρετικά ευαίσθητο στούς υπέρτονους και συνδυασμούς των δονήσεων που απαντούν στις υψηλότερες συχνότητες του μέσου υπερύθρου δηλ. των δονήσεων C-H, N-H και O-H. Για παράδειγμα, τό φάσμα NIR μείγματος πολυαιθυλενίου με θειικό λίθιο θα κυριαρχείται από το φάσμα του πρώτου συστατικού. Το θειικό λίθιο, με ισχυρότατη κορυφή περί τους 1100 cm-1, θα εμφανίσει στο ΝΙR μόλις τον εξαιρετικά ασθενικό τέταρτο υπέρτονο περί τους 4100 cm-1, o οποίος θα καλύπτεται από την πολύ ισχυρότερη δόνηση συνδυασμού του πολυαιθυλενίου.β) Η συνύπαρξη υπερτόνων και δονήσεων συνδυασμού στο
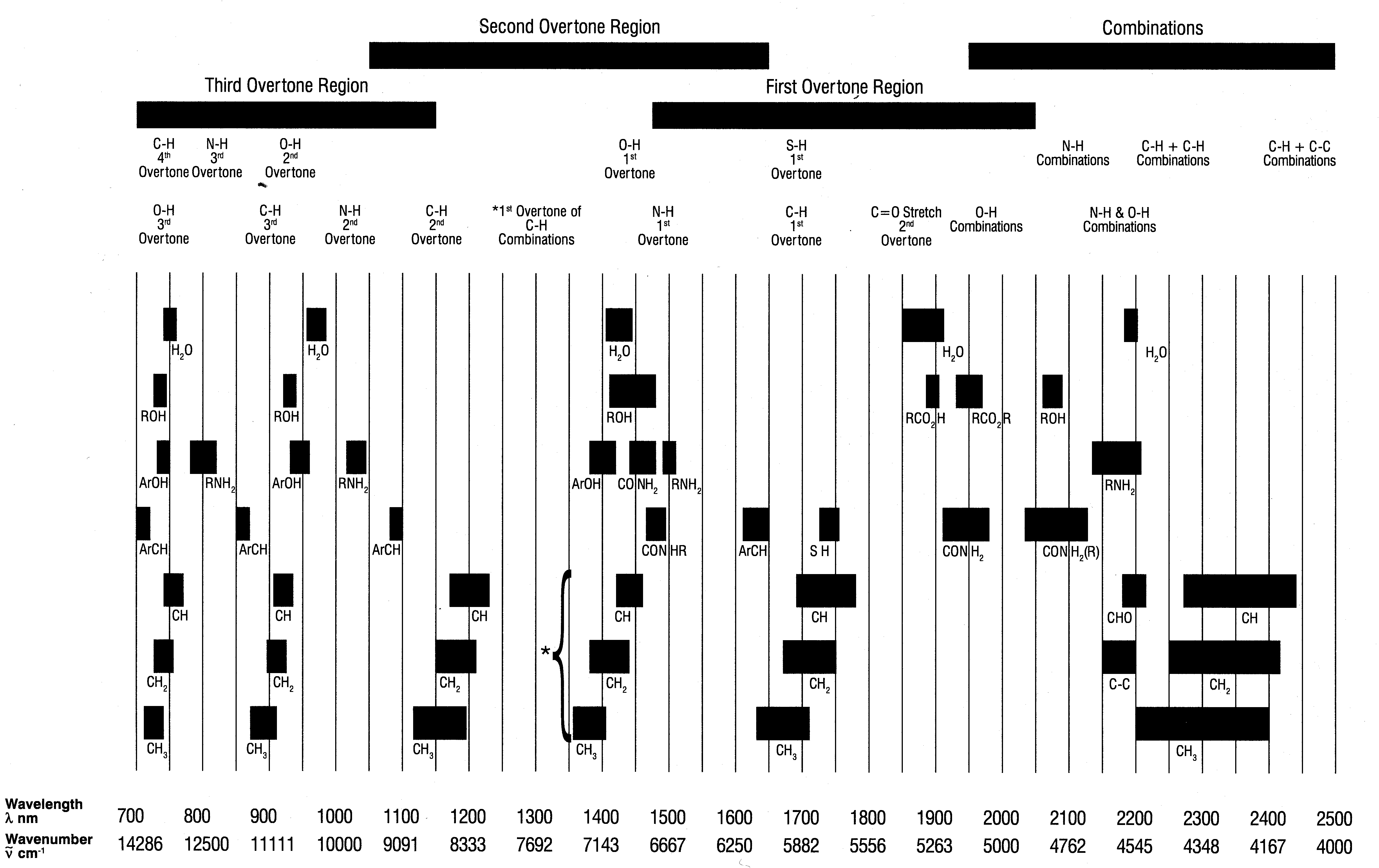
NIR, καθώς ο μεταβαλλόμενος βαθμός αναρμονικότητας, καθιστούν δύσκολη ή και αδύνατη την αναλυτική απόδοση κορυφών σε υλικά με πολύπλοκο φάσμα. Λίγες περιοχές του φάσματος αποτελούν ασφαλή ένδειξη ύπαρξης συγκεκριμένων χαρακτηριστικών ομάδων. Οι κυριότερες από αυτές συνοψίζονται στον ακόλουθο Πίνακα Α.
Πίνακας Α
Δονήσεις χαρακτηριστικών ομάδων στό εγγύς υπέρυθρο
Β. Στοιχεία οργανολογίας. Πλεονεκτήματα τεχνικών
NIR. Εφαρμογές.Υπάρχουν τριών ειδών φωτόμετρα
NIR με αυξανόμενο βαθμό δυνατοτήτων και εφαρμογών. Η πρώτη κατηγορία επιλέγει μέσω φίλτρων στενή περιοχή του φάσματος της πηγής NIR που αντιστοιχεί π.χ. στην περιοχή 2ν του νερού. Ο ανιχνευτής μετρά την συνολική διαπερατότητα σε αυτήν την περιοχή. Συσκευές αυτού του τύπου μπορούν να χρησιμοποιηθούν π.χ. για τον προδιορισμό υγρασίας σε τρόφιμα, στο χαρτί κλπ., αλλά δεν έχουν την δυνατότητα να ανιχνεύσουν χημικές αλλαγές στο υλικό οι οποίες συχνά συνεπάγονται μετατόπιση των χαρακτηριστικών κορυφών.Η δεύτερη κατηγορία διαθέτει μονοχρωμάτορα και συνεπώς παρέχει την φασματική πληροφορία συναρτήσει του μήκους κύματος. Ο χρόνος συλλογής του φάσματος εξαρτάται από την επιθυμητή διακριτική ικανότητα, αλλά πάντως είναι της τάξεως των αρκετών λεπτών.
Η τρίτη κατηγορία χρησιμοποιεί συμβολόμετρα και μετασχηματισμό
Fourier (δες Ασκηση 1). Η συλλογή δεδομένων μιάς σάρωσης με διακριτική ικανότητα 8 cm-1, γίνεται σε χρόνο της τάξεως του 0.5 sec, ενώ 5-30 σαρώσεις δίνουν συνήθως φάσμα με ικανοποιητικό λόγο σήματος πρός θόρυβο.Κύριο πλεονέκτημα της οργανολογίας
NIR είναι η συμβατότητα με την τεχνολογία οπτικών ινών χαμηλού κόστους. Τυπικά, ένα σύγχρονο φωτόμετρο FT-NIR μπορεί να διαθέτει 2-8 οπτικές ίνες με κατάλληλες κεφαλές μή καταστροφικής δειγματοληψίας σέ ισάριθμα σημεία που μπορούν να απέχουν περισσότερο από 100 m από την κεντρική μονάδα (χώρους παραλαβής πρώτων υλών, αντιδραστήρες, γραμμές παραγωγής ή συσκευασίας, αποθήκη κλπ).Η υψηλή ποιότητα τού σήματος με μικρό χρόνο δειγματοληψίας, η απουσία προετοιμασίας του δείγματος σε συνδυασμό με την συλλογή δεδομένων μέσω οπτικών ινών, καθώς και η πρόοδος των υπολογιστικών τεχνικών έχουν ανάγει την φασματοσκοπία
NIR σε ανερχόμενο εργαλείο βιομηχανικής έρευνας. Το εύρος των εφαρμογών καταδεικνύεται από την ακόλουθη σταχυολόγηση:
2. ΠΕΙΡΑΜΑΤΙΚΟ ΜΕΡΟΣ
Στην Ασκηση αυτή, θα χρησιμοποιήσουμε τεχνικές φασματοσκοπίας εγγύς υπερύθρου για να ταυτοποιήσουμε και να χαρακτηρίσουμε με μη καταστροφικό τρόπο πλαστικά φιαλίδια που χρησιμοποιούνται στην συσκευασία φαρμάκων.
Α. Τα δείγματα
Θα χρησιμοποιήσουμε τέσσερα πλαστικά φιαλίδια, συμπολυμερή του πολυαιθυλενίου χαμηλής πυκνότητας με πολυπροπυλένιο. Ο συμπολυμερισμός αυτός σε μεταβλητό βαθμό αποτελεί συνήθη τρόπο προσαρμογής των θερμικών, μηχανικών και χημικών ιδιοτήτων των πολυμερών στις προδιαγραφές που επιβάλλονται από τον χρήστη. Τρία από τα δείγματα έχουν γνωστή σύσταση, το τέταρτο θα αντιμετωπισθεί ώς άγνωστο:
(α) 100% πολυαιθυλένιο χαμηλής πυκνότητας (100
LDPE)(b
) 80% πολυαιθ. χαμ. πυκν. – 20% πολυπροπυλένιο (80LDPE-20PP)(γ) 100% πολυπροπυλένιο (100
PP)(δ) άγνωστο (
X)
Β. Μεθοδολογική προσέγγιση. Συλλογή δεδομένων
Με δεδομένη την ανάγκη μή καταστροφικού χαρακτηρισμού των δειγμάτων θα χρησιμοποιήσουμε οπτική ίνα με κεφαλή ανακλαστικότητας διαχύσεως. Η ίνα προσδιορίζεται ως τύπου Υ. Αποτελείται από δέσμη λεπτών οπτικών ινών, οι μισές από τις οποίες μεταφέρουν το διαμορφωμένο οπτικό σήμα του συμβολόμετρου στό δείγμα, ενώ οι υπόλοιπες συλλέγουν την σκεδαζόμενη ακτινοβολία και την κατευθύνουν στον ανιχνευτή. Θα επιλέξουμε τις καταλληλότερες συνθήκες δειγματοληψίας βελτιστοποιώντας την διακριτική ικανότητα (
resolution) και τον αριθμό των σαρώσεων κάθε φάσματος. Υψηλή διακριτική ικανότητα (π.χ. res.=2 cm-1) υποβοηθεί την διάκριση επικαλυπτόμενων κορυφών αλλά χειροτερεύει την ποιότητα του σήματος αυξάνοντας το επίπεδο θορύβου. Μεγάλοι αριθμοί σαρώσεων (π.χ. >50) δεν είναι πρακτικοί όταν η ίνα εφαρμόζεται στό δείγμα με το χέρι.Από κάθε δείγμα θα συλλέξουμε έναν αριθμό φασμάτων ώστε να αξιολογήσουμε στατιστικά τα φασματικά χαρακτηριστικά που πραγματικά οφείλονται στην χημεία του υλικού (π.χ. σύσταση, διαμόρφωση κλπ), και δεν αποδίδονται στην τυχαιότητα που εισάγει ο τρόπος δειγματοληψίας.
Κατόπιν θα διερευνήσουμε την δυνατότητα διάκρισης των τεσσάρων δοκιμίων μέσω των φασμάτων
NIR. Εάν απαιτηθεί θα βελτιώσουμε την στατιστική κάθε δείγματος είτε αυξάνοντας τον αριθμό των φασμάτων, είτε επιλέγοντας στοιχεία του φάσματος τα οποία είναι πλουσιότερα στην πληροφορία εκείνη που διαφοροποιεί τα δείγματα. Θα είμαστε συνεπώς σε θέση να διαμορφώσουμε μια μεθοδολογία ταυτοποίησης του κάθε τύπου δείγματος με βάση το φάσμα NIR.Τέλος, θα χρησιμοποιήσουμε τα τρία γνωστά δείγματα ως πρότυπα για να βαθμονομήσουμε μιά φασματοσκοπική μεθοδολογία ποσοτικού προσδιορισμού της σύστασης άγνωστων συμπολυμερών
LDPE-PP. Θα αξιοποιήσουμε την μεθοδολογία αυτή στον προσδιορισμό της σύστασης του δείγματος (δ).
Γ. Στατιστική επεξεργασία. Ομαδοποίηση φασμάτων. Ποσοτικοποιήσεις.
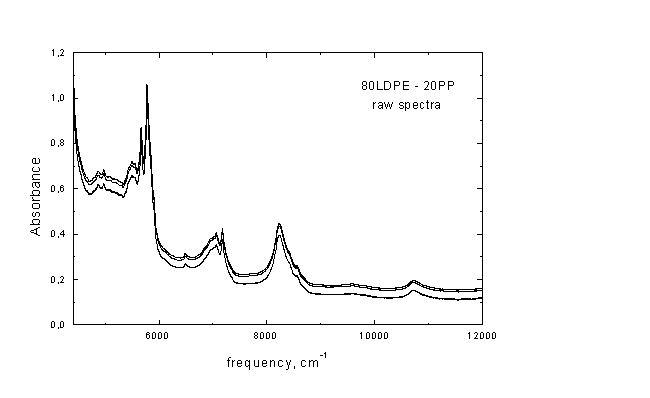
Στην Εικόνα Γ1 φαίνονται επτά φάσματα του δείγματος 80
LDPE – 20PP. Εχουν συλλεγεί με διακριτική ικανότητα 8 cm-1, και το κάθε ένα παριστά τον μέσο όρο 15 σαρώσεων. Ως υλικό αναφοράς έχει χρησιμοποιηθεί Teflon τύπου Spectralon. Παρά τα κοινά χαρακτηριστικά τους, τα φάσματα παρουσιάζουν εμφανείς διαφορές ως πρός την απόλυτη ένταση της απορρόφησης, γεγονός που πρέπει να οφείλεται κατ’ αρχήν στις όχι απολύτως επαναλήψιμες συνθήκες δειγματοληψίας.Ο καλύτερος τρόπος εξάλειψης τέτοιων χημικά μη σημαντικών διαφοροποιήσεων είναι η ανυσματική κανονικοποίηση των φασμάτων (
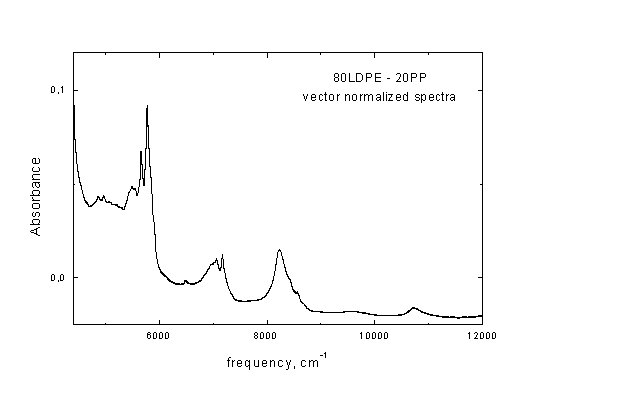
vector normalization). Κατ’ αυτήν επιλέγεται πρώτα η χρήσιμη φασματική περιοχή (εδώ 4300-12000 cm-1, κοινή και για τα επτά φάσματα) και υπολογίζεται η μέση τιμή της απορρόφησης κάθε φάσματος (yav) που παρατηρείται σε αυτήν. Η μέση τιμή αφαιρείται από τις μετρημένες τιμές της απορρόφησης, και έτσι το κάθε φάσμα τέμνεται από τον άξονα y=0. Yπολογίζεται το αθροισμα των τετραγώνων (y-yav)2, και το φάσμα διαρείται με την τετραγωνική ρίζα του αθροίσματος Σ(y-yav)2. Στον n-διαστατο χώρο (οπου n ο αριθμός των δεδομένων – σημείων), το ανυσματικό μέτρο του φάσματος ισούται πλέον με την μονάδα. Στην Εικόνα Γ2 περιλαμβάνονται τα επτά φάσματα της Εικόνας Γ1, μετά από ανυσματική κανονικοποίηση. Είναι προφανές ότι η συγκεκριμένη προκατεργασία του κάθε φάσματος βελτιώνει σημαντικά την επαναληψιμότητα των μετρήσεων.Εικόνα Γ1
Εικόνα Γ2
Στην Εικόνα Γ3 δίδονται οι μέσοι όροι των ανυσματικά κανονικοποιημένων φασμάτων των τεσσάρων δειγμάτων (α) – (δ).
Εικόνα Γ3
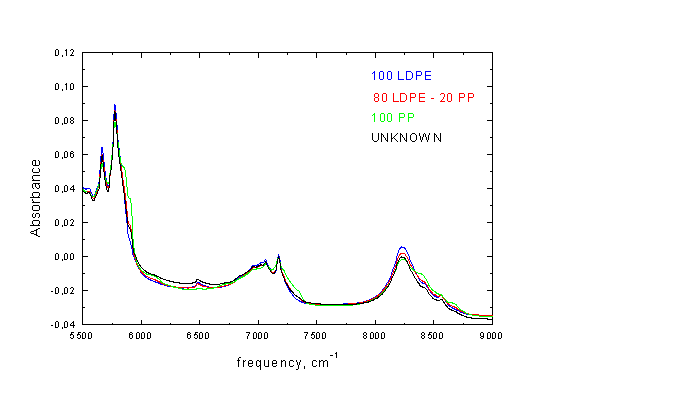
Οι διαφορές μεταξύ των φασμάτων είναι μικρές. Η παρουσία του πολυπροπυλενίου προκαλεί την ενίσχυση της απορρόφησης στις υψηλότερες συχνότητες των περιοχών 5600-6000
cm-1 (2νCH), 6800-7400 cm-1 (2νCH+δCH) και 8000-8800 cm-1 (3νCH). Η τάση αυτή είναι συμβατή με την χημεία του συστήματος διότι η παρουσία του πολυπροπυλενίου αυξάνει την συγκέντρωση μεθυλομάδων –CH3, οι οποίες δονούνται σε υψηλότερες συχνότητες από τις μεθυλενικές =CH2 (δες Πίνακα Α). Η επίδραση της συγκέντρωσης πολυπροπυλενίου στό φάσμα είναι περισσότερο εμφανής στην 2η παράγωγο των φασμάτων της Εικόνας Γ3 (Εικόνα Γ4).Εικόνα Γ4
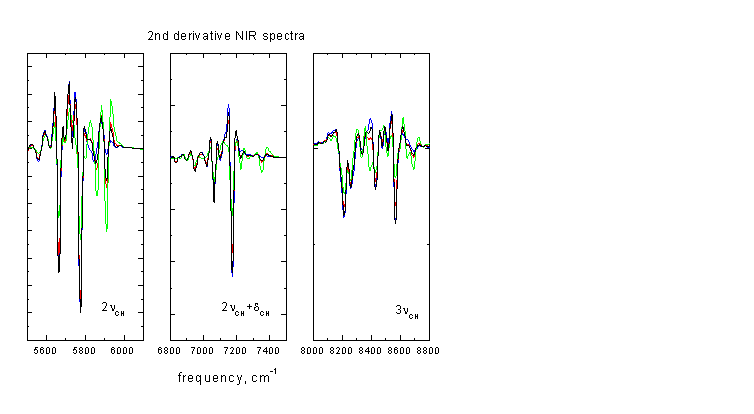
Η παραγώγιση των φασμάτων είναι συνήθης μαθηματική επεξεργασία όταν είναι επιθυμητή η φαινομενική αύξηση της διακριτικής ικανότητας των φασμάτων. Η δεύτερη παράγωγος Λορεντζιανής καμπύλης έχει ημιεύρος ίσο με το 32.6% αυτού της Λορεντζιανής, και η τέταρτη, ίσο με το 20.8%. Ωστόσο, η παραγώγιση των φασμάτων έχει δύο σημαντικά μειονεκτήματα, και γι αυτό πρέπει να χρησιμοποιείται με προσοχή: Η ένταση του σήματος της 2ης παραγώγου είναι σηνάρτηση του ημιεύρους της ταινίας. Συνεπώς το φάσμα 2ης παραγώγου τονίζει τις οξείες κορυφές (π.χ. αυτές που αντιστοιχούν σε κρυσταλλίτες) και υποβαθμίζει τις ευρείες. Το δεύτερο μειονέκτημα σχετίζεται με την υποβάθμιση του λόγου σήματος πρός θόρυβο κατά τον παράγοντα 2
n, όπου n η τάξη της παραγώγου.Εχοντας επιλέξει τις καταλληλότερες συνθήκες συλλογής και επεξεργασίας του φάσματος (διακριτική ικανότητα 8
cm-1, 15 σαρώσεις ανά φάσμα, ανυσματική κανονικοποίηση, 2η παράγωγο, φασματικές περιοχές 5500-6200 cm-1, 6800-7500 cm-1 και 8000-8800 cm-1), απομένει να διαρευνήσουμε κατά πόσον η επαναληψιμότητα των φασμάτων κάθε δοκιμίου επιτρέπει την διάκριση των τεσσάρων δειγμάτων. Ο απλούστερος τρόπος είναι η διερεύνηση της ομαδοποίησης (clustering) όλων των επί μέρους φασμάτων, και η σύγκρισή της με την ομαδοποίηση που επιβάλλουν τα διαφορετικά δείγματα.Οι εφαρμογές ομαδοποίησης περιλαμβάνουν τα ακόλουθα στάδια:
α) Καταστρώνεται κατάλογος όλων των επι μέρους φασμάτων που έχουν υποστεί την κατάλληλη μαθηματική προκατεργασία α
1, α2 ... αn, β1, ... βn, γ1, ... γν, ..., όπου α, β, γ, ..., τα διαφορετικά δείγματα.β) Υπολογίζονται οι αποστάσεις
Dij μεταξύ όλων των δυνατών ζευγών φασμάτων. Υπάρχουν πολλοί τρόποι υπολογισμού των αποστάσεων αυτών. Eδώ θα χρησιμοποιήσουμε τον φορμαλισμό:γ) Τα δύο φάσματα με την μικρότερη μεταξύ τους απόσταση ομαδοποιούνται σε ένα
clusterδ) Υπολογίζονται οι αποστάσεις μεταξύ του
cluster και των υπολοίπων φασμάτων. Οι μικρότερη απόσταση φάσματος-φάσματος, φάσματος – cluster ή cluster - cluster, οδηγεί σε νέες ομαδοποιήσεις.ε) Η διαδικασία (δ) συνεχίζεται μέχρι να απομείνει ένα μόνο
clusterΟ καλύτερος γραφικός τρόπος παρουσίασης των αποτελεσμάτων της ομαδοποίησης είναι με το ακόλουθο δενδρόγραμμα Εικόνα Γ5:
Εικόνα Γ5

Ο δείκτης «ανομοιογένεια» (
heterogeneity) αναφέρεται στις αποστάσεις D που επιτρέπουν την διάκριση κλάδων του δένδρου. Η πρώτη δέσμη κλάδων (πάνω μέρος της Εικόνας Γ5) περιλαμβάνει 11 φάσματα από τρία διαφορετικά δοκίμια με την ίδια σύσταση: 100 LDPE. Η τελευταία ενσωμάτωση κλάδου στην δέσμη αυτή έγινε με απόσταση 0.23, ενώ η επόμενη δέσμη απέχει κατά 1.9. Αυτή η διαφορά μεταξύ αποστάσεων εντός της δέσμης και μεταξύ δεσμών επιτρέπει την στατιστικά σαφή διάκριση της δέσμης από το υπόλοιπο δένδρο. Με πιό προσεκτική παρατήρηση η δέσμη 100 LDPE θα μπορούσε να διακριθεί σε δύο υποδέσμες, μία που περιλαμβάνει φάσματα των φιαλών 1 και 3, και άλλη που αντιστοιχεί αποκλειστικά στην φιάλη 2. Η διαφορά είναι πραγματική και θα μπορούσε να οφείλεται σε διαφορετική παρτίδα του ιδίου δείγματος, γήρανση κλπ.Τό μέσο τμήμα του δενδρογράμματος κυριαρχείται από δύο δέσμες κλάδων με απόσταση μεταξύ τους ίση με 0.89. Οι δέσμες αντιστοιχούν στο δείγμα 80
LDPE – 20 PP, και στό άγνωστο. Η απόσταση μεταξύ των δεσμών είναι σαφως μεγαλύτερη από τις μέγιστες αποστάσεις των κλάδων στο εσωτερικό κάθε δέσμης (0.03 και 0.32, αντίστοιχα), και επιτρέπουν την ασφαλή διάκριση και αυτών των συστάσεων.Τέλος, το κατώτερο τμήμα του δενδρογράμματος που περιλαμβάνει φάσματα δοκιμίων μέ σύσταση 100
PP, απέχει σημαντικά (5.9) από τους προηγούμενους κλάδους. Η διάκρισή του είναι σαφής και αυτονόητη.Η κατάστρωση δενδρογράμματος είναι ο ασφαλέστερος μαθηματικά επαρκής τρόπος διερεύνησης των συσχετισμών που ενυπάρχουν σε φασματικές βάσεις δεδομένων. Χρησιμοποιείται πάντα σε σύγκριση με εξωτερικά ιεραρχικά κριτήρια διάκρισης, όπως:
Ο καθορισμός των κριτηρίων αυτών είναι ίσως το κρισιμότερο στάδιο των εφαρμογών ταυτοποίησης. Καθορίζουν όχι μόνο την χρησιμότητα της μεθόδου αλλά και τον όγκο της επεξεργασίας που απαιτείται για την κατάστρωσή της. Για τον λόγο αυτό, τα κριτήρια διάκρισης ορίζονται με βάση το αποδεκτό εύρος τιμών των ιδιοτήτων ενός υλικού, δηλ. με βάση τις προδιαγραφές που αυτό πρέπει να πληροί.
Αντίστροφα, το δενδρόγραμμα μπορεί να χρησιμοποιηθεί για την βελτιστοποίηση των παραμέτρων συλλογής και προκατεργασίας του φάσματος, ώστε να πληρούνται οι προϋποθέσεις διάκρισης με βάση ένα συγκεκριμένο από τα παραπάνω κριτήρια (π.χ. το τελευταίο, το οποία με τις παρούσες συνθήκες δεν επιτυγχάνεται).
Εχοντας καταδείξει την δυνατότητα φασματοσκοπικής διάκρισης των τεσσάρων συστάσεων, και συνεπώς την δυνατότητα ασφαλούς ταυτοποίησής τους, μένει να διερευνήσουμε αν τα φάσματα
NIR επιτρέπουν τον ποσοτικό προσδιορισμό της σύστασης του αγνώστου δείγματος. Θα αξιοποιήσουμε τα ακόλουθα δείγματα – φάσματα ως πρότυπα:
|
x, % LDPE |
y, % PP |
|
|
(α) |
100 |
0 |
|
(β) |
80 |
20 |
|
(γ) |
0 |
100 |
Οι συγκεντρώσεις
LDPE και PP χρησιμοποιούνται ως ανεξάρτητες διότι το άγνωστο δείγμα θα μπορούσε στην γενική περίπτωση να περιέχει περισσότερα των δύο συστατικά.Πρέπει να διευκρινισθεί ότι η κατάστρωση αξιόπιστης μεθοδολογίας ποσοτικού προσδιορισμού έστω και ενός συστατικού θα απιτούσε τουλάχιστον μια εικοσάδα προτύπων με διαφορετική περιεκτικότητα %
PP. Ο μικρός αριθμός των προτύπων χρησιμοποιείται εδώ αποκλειστικά για λόγους επίδειξης.Η ποσοτικοποίηση γίνεται συνήθως με μαθηματικές μεθόδους πολυπαραμετρικής ανάλυσης (
multivariate analysis), οι οποίες αποτελούν χημειομετρικά εργαλεία. Τα φάσματα των προτύπων (εδώ, Φ(α), Φ(β), Φ(γ)) αντιμετωπίζονται ως ανύσματα τα οποία μπορούν να εκφρασθούν ως γραμμικοί συνδυασμοί των ανυσμάτων μιάς νέας βάσης (φ(α), φ(β), φ(γ)) με συντελεστές τις διαθέσιμες γνωστές παραμέτρους (εδώ, τις περιεκτικότητες x LDPE, y PP).Φ
= χφΟ υπολογισμός του ανύσματος φ με βάση τα φάσματα των προτύπων επιτρέπει τον προσδιορισμό της παραμέτρου χι από το φάσμα του αγνώστου δείγματος Φι
.Εφαρμογή της μεθοδολογίας αυτής στο άγνωστο δείγμα (δ) δίνει την σύσταση
LDPE = 90.7%
PP = 9.3%
To
γεγονός ότι οι περιεκτικότητες των δύο συστατικών αθροίζουν στο 100% παρότι αντιμετωπίστηκαν σαν ανεξάρτητες μεταβλητές, υποδηλώνει ότι το άγνωστο δείγμα δεν περιέχει περισσότερα συστατικά. Τέλος, σημειώνεται ότι η ίδια μεθοδολογία εφαρμοζόμενη σε ομόλογες σειρές δειγμάτων θα μπορούσε να χρησιμοποιηθεί για τον προσδιορισμό και μη-χημικών παραμέτρων (πυκνότητα, ιξώδες, θερμοκρασία υαλώσεως, σκληρότητα κλπ.)
Η ΦΑΣΜΑΤΟΣΚΟΠΙΑ ΥΠΕΡΥΘΡΟΥ ΣΤΟ ΔΙΑΔΙΚΤΥΟ
Μια επίσκεψη στο διαδίκτυο με τις συνηθισμένες μηχανές αναζήτησης και με λέξεις-κλειδιά
infrared (ή IR) spectroscopy, spectral databases, chemometrics, tutorial ή virtual classroom, αποδίδει πληθώρα σελίδων με ενδιαφέρουσες γενικές ή ειδικές πληροφορίες. Μερικές τέτοιες σελίδες με γενικότερο ενδιαφέρον που ήταν ανοικτές τον καιρό της προετοιμασίας αυτών των σημειώσεων (Ιούλιος 1999) σταχυολογούνται παρακάτω. Μήν αρκεστείσε σ’ αυτές, το περιεχόμενο του διαδίκτυου διευρύνεται και ανανεώνεται συνεχώς.Vibrational spectroscopy
www.ijvs.com/index.htmlΗλεκτρονικό περιοδικό δονητικής φασματοσκοπίας. Κάθε τεύχος περιλαμβάνει γενικά εισαγωγικά άρθρα (
feature articles) αλλά και κανονικές ερευνητικές δημοσιεύσεις. Καλύπτει και την φασματοσκοπία Raman.Infrared spectroscopy
chipo.chem.uic.edu/web1/ocol/spec/IR.htm
Σελίδα του
Univ. of Illinois, με μιά γενική εισαγωγή στην φασματοσκοπία υπερύθρου και την χρήση της στον χαρακτηρισμό οργανικών υλικών. Περιέχει παραδείγματα – ασκήσεις.chemistry.gsu.edu/post_docs/koen/wir.html
wwwchem.csustan.edu/quickir.htm
Σύντομες εισαγωγές στην φασματοσκοπία υπερύθρου. Ενδιαφέροντα
links.Chemometrics
ourworld.compuserve.com/homepages/catbar/mva_def.htm
ull.chemistry.uakron.edu/chemometrics/index.html
www.camo.no/Applications/MultivariateAnalysis.htmlΤρείς σελίδες με την μαθηματική θεμελίωση των χημειομετρικών μεθόδων ανάλυσης δεδομένων.
IR databases
webbook.nist.gov/chemistry/
www.galactic.com/scponlineΔύο ελεύθερες βάσεις αναζήτησης φασμάτων υπερύθρου.
H εισαγωγή δεδομένων γίνεται μέσω του ονόματος της χημ. ένωσης, του μοριακού τύπου, του μοριακού βάρους, ή, ευκολότερα, μέσω του αριθμού CAS. www.chem.uni-potsdam.de/tools/index.htmlΕισάγετε την θέση μιας κορυφής υπερύθρου σε
cm-1 και αναζητείτε την πιθανή προέλευσή της.newsgroups
Sci.techniques.spectroscopy