
Potential and Kinetic Energy Diagrams -- Large Objects
Drawing Potential Energy Diagrams
Potential Energy Diagrams -- Small Objects
Determining Wavelengths -- General
Determining Wavelengths -- Example
Constraints on the Wave Function: An Infinite Potential Energy Example
Constraints on the Wave Function: A Finite Potential Energy Example
Decreasing Wave Functions -- Qualitative
Decreasing Wave Functions -- Quantitative
Rules For Drawing Wave Functions

where h is Planck's Constant (6.63E-34 J s = 4.14E-15 eV s), named for Max Planck.
However, the wave function is not identical to results obtained using equations such as Force = mass × acceleration. With a result which comes from Newton's Laws, we obtain precise information about the location of the object at any future time. All we need to know are the forces acting on it, its present location, and its present velocity; all other information regarding the future motion of the object is then determined. Schrödinger's Equation, on the other hand, can only provide us with information about the probability of finding the object in each location at some future time. We can state that the probability of finding the object at each point is high or low, but we can never say with certainty where the object will be at a future time.
The study of the behavior of small objects such as electrons by using Schrödinger's Equation is usually called Quantum Mechanics.
The total probability that the object is "somewhere" is 1. The area under a probability versus position curve must therefore equal 1. For the wave function shown here, the probability of the object being somewhere between locations x1 and x2 is equal to the area of the small rectangle under the probability curve bounded by x1 and x2.
As an example of using energy to describe motion, consider a small cart moving on a level, very low-friction surface. If we ignore the friction entirely, then the cart always has whatever energy it had at the beginning of its motion. No potential energy exists in this case, so the total energy is equal to the kinetic energy; the potential energy is zero. A simple graph or diagram describes this situation.
In a real situation, even on an air track, the cart does not go on forever. Instead, it strikes the end of the track and turns around. With a perfect collision at the end of the track, the cart would have the same kinetic energy before and after the collision with the end; only the direction would change. However, during the collision the cart's speed decreases to zero. Plotting kinetic energy versus distance, we get another diagram.
Looking at the end of the track, we see what happens during the collision. The flexible steel springs on the cart and track bend. This process increases the elastic potential energy, resulting in a different diagram.
We can combine kinetic, potential, and total energies for this situation into a single diagram.
Consider the question: For each value of kinetic energy, how far will the metal on the ends compress? The first step in our answer is to draw the potential energy diagram for the situation. It looks like the first of the three diagrams above. The high sides indicate that the potential energy gets very large at the ends of the track. Now pick a value for kinetic energy. What is the furthest location to the left that the cart will reach? Why?
Now we add a magnet on the track and on the cart so that the magnets attract. Look at the kinetic energy diagram for the cart. The total energy does not change, so the potential energy must be as shown here. For most situations, we can draw a potential energy diagram by following similar reasoning patterns.
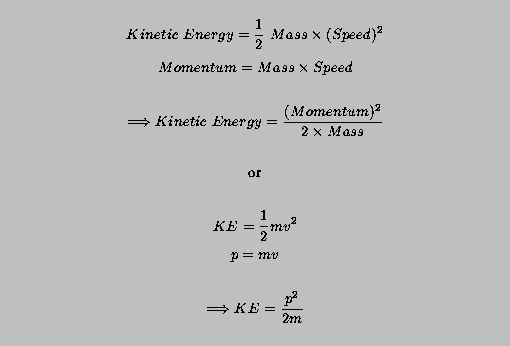
Then, we can use these equations with the wavelength-momentum relation to write the wavelength in terms of the kinetic energy.

We can use this equation for any object. To describe an electron using units of electron volts (eV) for energy and nanometers (nm) for wavelength, the equation above becomes

We can use this result to find the wavelength of the wave function in each region of potential energy. In general we will not calculate the exact number for the wavelength. Instead, we will want to know how the wavelength in one region compares to that in another. For that comparison we can use the equation above to note that
as the kinetic energy goes up the wavelength goes down and
as the kinetic energy goes down the wavelength goes up.
Looking at the equation, we can also see that the kinetic energy must be positive for the wavelength to have any meaning. If the kinetic energy is negative, we get the square root of a negative number. That gives us a meaningless wavelength. Thus, we can use this result only for positive kinetic energies. That is: when the total energy is greater than the potential energy.
This discussion leads to our second rule for obtaining solutions to Schrödinger's Equation:
To determine the kinetic energy of the electron we look at the difference between the total energy and the potential energy. As shown in the next figure, the kinetic energy on the left side is about four times greater than that on the right side of the edge of the metal.
So, we conclude that the wavelength on the left side will be about one-half of that on the right side. The approximate wave function looks like the one in this figure.
If we approach this boundary from the left, we obtain the probability marked as A. However, if we approach from the right we get a different probability (B) at the boundary. A different value occurs depending on which way we approach the boundary, yet it is the same boundary. Two different values for the probability at the same point would be meaningless. So, we have another rule, called the smoothness condition, for drawing wave functions:
If the object cannot get out of this box, we know that the probability of finding the electron outside the box must be zero. That leads us to the conclusion that the wave function is zero outside the box. Because of the smoothness condition, wave functions inside the box must approach zero as they get near to the edges of the box. These nodes at the edge of the box represent a constraint on the wave function.
With this constraint in mind, we will create some wave functions for the object in this box. Inside the box the potential energy is zero, so the kinetic energy is equal to the total energy. First, we will pick an energy and see what we get. The process will be easier if we use numbers with units of electron-volts and nanometers. In particular, we will use a length of 0.2 nm for our box.
As a starter, we will see what happens with a kinetic energy of 6 eV. Calculating the wavelength we have:

The wavelength here is two and a half times the length of the box. Drawing this wave within the boundaries of the box gives a picture which looks like this.
This wave function has problems because it cannot meet the constraints of going to zero on the edges of the box. Thus, we must eliminate this wave function as one of the possibilities.
Based on this experience, it makes some sense to work backwards from the way we have been. Sketch waves that fit in the box, then determine the energies which will match those waves. Waves which meet the zero condition at the edge and the smoothness condition are similar to standing waves on a string. The following diagram shows several possibilities for these wave functions.
With the constraint that the wave function must be zero on the edges of the box, only certain wave functions are allowed in the box. These wave functions must have wavelengths such that they fit in the box. Just as the standing wave on a string, the wave functions which fit can have wavelengths equal to half the length of the box, the length of the box, one and a half times the length of the box, twice the length of the box, and so forth.
Because the energy of a wave is related to its wavelength, such an object is allowed to have only certain energies. Since only certain values of energy result in allowed wave functions, these systems are said to be "quantized." Thus, the name "quantum mechanics" is associated with systems which have only certain values of energy. We see evidence for this quantization of energy in the light emitted by atoms.
To determine the wave functions, we will need to think through what could happen. First, we know the results for an infinite potential energy. Suppose that the potential energy were just a little less than infinite. (Say, infinity - 2, whatever that means.) We would not expect much change in the wave functions from the infinite potential energy, because the potential energy is only slightly less. We also know that the object will have a low probability of being in locations which are very far away from the box.
Studies of waves tell us that when the potential energy changes as in
this case, the wave function decreases to zero quickly in the region of large
potential energy. Thus, one possibility is for the wave function to
look similar to standing waves inside the box but to decrease to zero
quickly as it leaves the box. These wave functions are shown in the
following figure.
We would also expect that, for a given total energy, the rate of
decrease should depend on the size of the potential energy. If the
potential energy is large, the object should be more restricted than
if it is small. The results show that this does occur as illustrated
here.
13. Decreasing Wave Functions -- Qualitative
In regions where the total energy is less than the potential energy,
the amplitude of the wave function decreases. Further away from the
boundary where the potential energy changes, the probability of the
object being located there decreases. However, in the region where the
total energy is less than the potential energy, the probability of
finding the object is not always zero.
14. Decreasing Wave Functions -- Quantitative
To put some numbers on the rate of decrease of the wave function in regions where the total energy is
less than the potential energy, we introduce some approximations based
on wave motion. First, we introduce a characteristic length, l, with
which we describe the decrease:

When we use the electron-volt and nanometer units, we obtain an equation similar to the one we used for wavelength.

We use this length as a unit to measure the decrease of the wave function's amplitude. The basic (approximate) rule is that when we move six times l in a region where PE > TE the amplitude of the wave function decreases to one-third of its value (see figure).
We can apply this rule to determine how much the wave function decreases in any region where the total energy is less than the potential energy.
Net force = mass × acceleration.
Every applied force results in a reaction force on the applier. This reaction force is equal in magnitude but opposite in direction to the applied force.




